- 1hive修改schema的location_hive location alter
- 2【随记】元学习
- 3uniapp项目实战+springboot的知识分享学习头条App[源码+文档+答疑+远程_uniapp小程序项目头条
- 4分布式计算概述_分布式计算是如何把一个任务分成许多小的部分
- 5内网渗透-smb&wmi_wmi渗透
- 6大数据最全深度学习(五)—— 卷积神经网络(CNN(3),2024年最新面试大数据开发卡顿_卷积神经网络数据集处理
- 7C语言字符串库常用函数_c语言 字符串长度 指定编码 计算函数
- 8程序员被公司辞退12天,前领导要求回公司讲清楚代码,结果蒙了_代码看不懂是否还和离职员工有关系
- 9Android 13 SystemUI 屏蔽导航栏;屏蔽锁屏;隐藏状态栏;禁止状态栏下拉;屏蔽Camera绿色图标;屏蔽原生音量条;屏蔽原生亮度条。_android 隐藏状态栏
- 10华为OD机试Js - 根据IP查找城市_某业务需要根据终端的ip地址获取该终端归属的城市,可以根据公开的ip地址池信息查
语音深度鉴伪识别项目实战:基于深度学习的语音深度鉴伪识别算法模型(三)音频去噪算法大全+Python源码应用
赞
踩
前言
深度学习技术在当今技术市场上面尚有余力和开发空间的,主流落地领域主要有:视觉,听觉,AIGC这三大板块。
目前视觉板块的框架和主流技术在我上一篇基于Yolov7-LPRNet的动态车牌目标识别算法模型已有较为详细的解说。与AIGC相关联的,其实语音模块在近来市场上面活跃空间很大。
从智能手机的语音助手到智能家居中的语音控制系统,再到银行和电信行业的语音身份验证,语音技术的应用日益广泛。那么对应现在ACG技术是可以利用原音频去进行训练学习,从而得到相对应的声音特征,从而进行模仿,甚至可以利用人工智能生成的语音可以以假乱真,给社会带来了严重的安全隐患。
当前,语音深度鉴伪识别技术已经取得了一定的进展。研究人员利用机器学习和深度学习方法,通过分析语音信号的特征,开发出了一系列鉴伪算法。
然而,随着生成大模型和其他语音合成技术的不断进步,伪造语音的逼真度也在不断提高,使得语音鉴伪任务变得愈加复杂和具有挑战性。本项目系列文章将从最基础的语音数据存储和详细分析开始,由于本系列专栏是有详细解说过深度学习和机器学习内容的,音频数据处理和现主流技术语音分类模型和编码模型将会是本项目系列文章的主体内容,具体本项目系列要讲述的内容可参考下图:
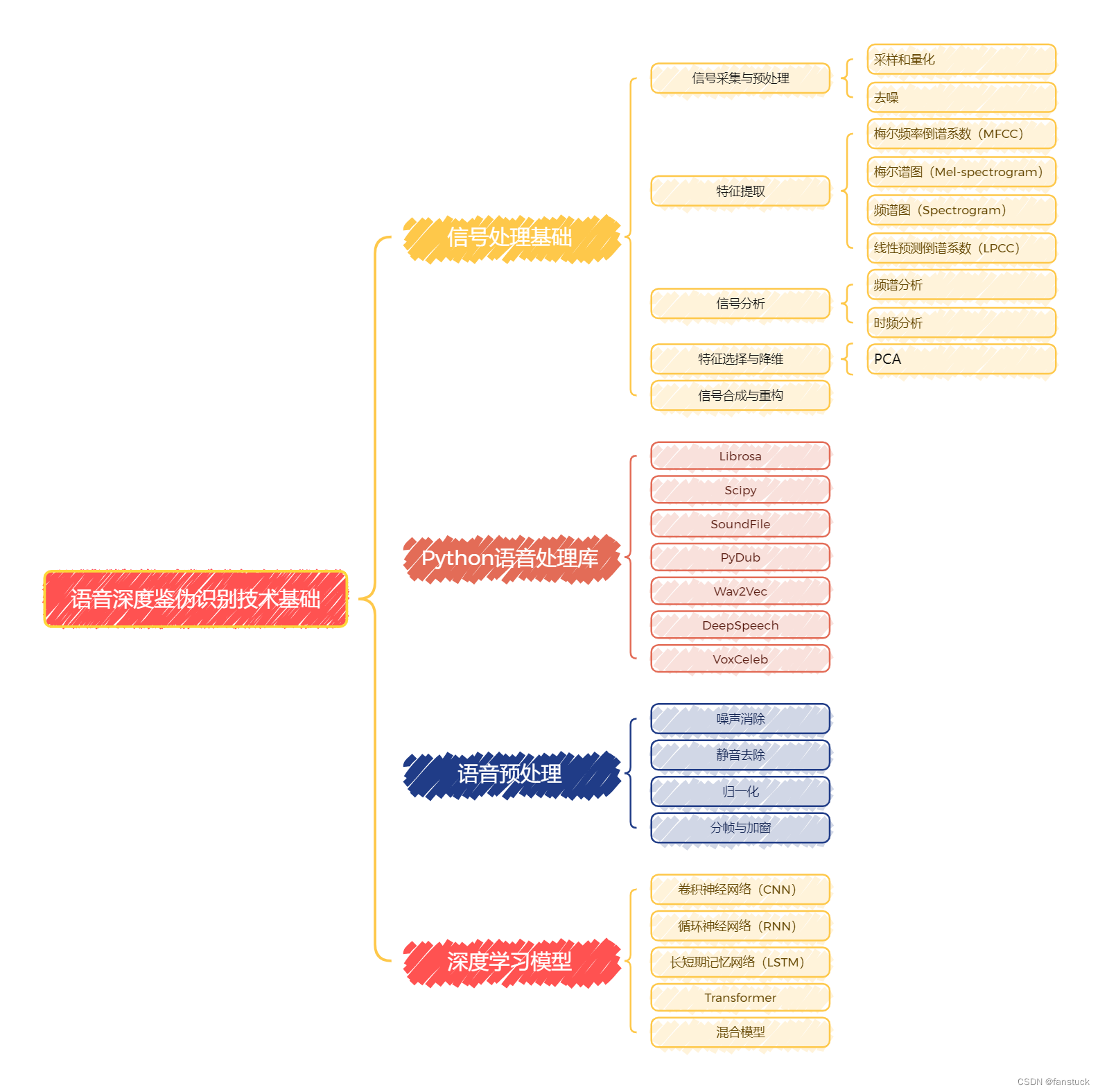 语音模型的内容不是那么好掌握的,包含大量的数学理论知识以及大量的计算公式原理需要推理。且如果不进行实际操作很难够理解我们写的代码究极在神经网络计算框架中代表什么作用。不过我会尽可能将知识简化,转换为我们比较熟悉的内容。
语音模型的内容不是那么好掌握的,包含大量的数学理论知识以及大量的计算公式原理需要推理。且如果不进行实际操作很难够理解我们写的代码究极在神经网络计算框架中代表什么作用。不过我会尽可能将知识简化,转换为我们比较熟悉的内容。
我将尽力让大家了解并熟悉神经网络框架,保证能够理解通畅以及推演顺利的条件之下,尽量不使用过多的数学公式和专业理论知识。以一篇文章快速了解并实现该算法,以效率最高的方式熟练这些知识。希望有需求的小伙伴不要错过笔者精心打造的专栏。
上篇文章详细解答了部份音频噪音种类和效果,以及频谱减法(Spectral Subtraction)和自适应滤波(Adaptive Filtering),接下来我们需要继续了解小波变换去噪(Wavelet Transform Denoising)和维纳滤波(Wiener Filter)进行去噪算法结尾。
小波变换去噪(Wavelet Transform Denoising)
小波变换是一种能够同时在时域和频域中对信号进行分析的技术。它利用小波函数对信号进行多尺度分解,能够有效地捕捉信号的局部特征和突变点。在去噪应用中,小波变换被广泛应用于处理各种类型的信号,如语音信号、图像、医学信号等。
详细步骤
1. 小波分解
对信号进行小波分解,可以得到不同尺度上的逼近系数和细节系数。公式如下:
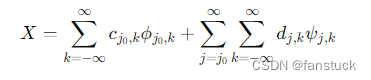
其中, ϕ j 0 k ϕ_{j_{0}k} ϕj0k是尺度函数, ψ j , k \psi_{j,k} ψj,k 是小波函数, c j v , k c_{j_v,k} cjv,k 和 d j , k d_{j,k} dj,k 分别是尺度系数和细节系数。
2. 阈值处理
对细节系数进行阈值处理,去除噪声。常见的阈值处理方法有:
- 硬阈值(Hard Thresholding):将小于阈值的系数置为零。
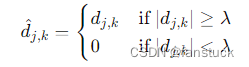
- 软阈值(Soft Thresholding):将小于阈值的系数置为零,大于阈值的系数按一定规则缩小。
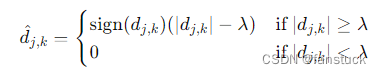
硬阈值是一种简单的置零的方法,而软阈值对于大于阈值的小波系数作了"收缩",即都减去阈值,从而使输入-输出曲线变成连续的。在阈值选选取上,人们普遍使用软阈值。改进的阈值是硬阈值和软阈值之间的一个折中,即当小波系数小于阈值时,不是简单地置为零,而是平滑地减小为零,当大于阈值时,小波系数幅度都减去阈值。这样,既保证了大的小波系数,又保证了加阈值后系数的平滑过渡。
阈值的选取
在小波变换去噪过程中,阈值选择至关重要,直接影响去噪效果。常用的阈值选择方法包括通用阈值(Universal Threshold)和自适应阈值。下面详细介绍这两种方法的计算逻辑。
1. 通用阈值(Universal Threshold)
通用阈值是由Donoho和Johnstone提出的一种简单有效的阈值选择方法。通用阈值的计算公式如下:
λ
=
σ
2
l
o
g
(
n
)
λ=σ\sqrt {2log(n)}
λ=σ2log(n)
其中:
-
σ \sigma σ 是噪声标准差。
-
估计噪声标准差:通常使用高频细节系数(如小波分解后的最后一级细节系数)的中值绝对偏差(MAD)来估计噪声标准差。
-
σ = m e d i a n ( ∣ d ∣ ) 0.6745 σ= \frac{median(∣d∣)}{0.6745} σ=0.6745median(∣d∣)
sigma = np.median(np.abs(coeffs[-level])) / 0.6745- 1
-
-
n n n 是信号的长度。
2.自适应阈值(SURE Thresholding)
自适应阈值(SURE,Stein’s Unbiased Risk Estimate)方法通过最小化估计风险(误差)来选择阈值。SURE方法可以针对不同尺度的系数单独选择阈值,更加灵活。
计算每个尺度的阈值:对于每个尺度的系数,计算一个最佳阈值。
计算SURE值:计算不同阈值下的SURE值,选择使SURE值最小的阈值。
def calculate_sure_threshold(coeff):
n = len(coeff)
sorted_coeff = np.sort(np.abs(coeff))
risks = np.zeros(n)
for i in range(n):
t = sorted_coeff[i]
risk = (n - 2 * (i + 1) + np.sum(np.minimum(coeff**2, t**2))) / n
risks[i] = risk
best_threshold = sorted_coeff[np.argmin(risks)]
return best_threshold
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
3. 小波重构
对处理后的系数进行逆小波变换,重构信号。逆变换公式与分解公式相反,利用处理后的系数进行信号重建。
# 小波重构
denoised_signal = pywt.waverec(coeffs_thresh, wavelet)
- 1
- 2
整体去噪代码:
def wavelet_denoising(signal, wavelet='db1', level=1, thresholding='soft'): # 小波分解 coeffs = pywt.wavedec(signal, wavelet, level=level) # 计算阈值 universal_threshold = calculate_universal_threshold(coeffs) # 阈值处理 coeffs_thresh = [] for i, c in enumerate(coeffs): if i == 0: # 保留逼近系数 coeffs_thresh.append(c) else: # 使用SURE阈值处理细节系数 sure_threshold = calculate_sure_threshold(c) if thresholding == 'hard': coeffs_thresh.append(pywt.threshold(c, sure_threshold, mode='hard')) elif thresholding == 'soft': coeffs_thresh.append(pywt.threshold(c, sure_threshold, mode='soft')) # 小波重构 denoised_signal = pywt.waverec(coeffs_thresh, wavelet) return denoised_signal def calculate_universal_threshold(coeffs): # 使用高频细节系数估计噪声标准差 sigma = np.median(np.abs(coeffs[-1])) / 0.6745 # 计算通用阈值 threshold = sigma * np.sqrt(2 * np.log(len(coeffs[-1]))) return threshold def calculate_sure_threshold(coeff): n = len(coeff) if n == 0: return 0 sorted_coeff = np.sort(np.abs(coeff)) risks = np.zeros(n) for i in range(n): t = sorted_coeff[i] risk = (n - 2 * (i + 1) + np.sum(np.minimum(coeff**2, t**2))) / n risks[i] = risk best_threshold = sorted_coeff[np.argmin(risks)] return best_threshold
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44

听音频效果去噪能力还是一般,比原音频要更加清晰一点。
维纳滤波(Wiener Filter)
维纳滤波(Wiener Filter)是由诺伯特·维纳提出的一种线性滤波方法,旨在通过最小化输出信号与期望信号之间的均方误差(MSE)来实现信号的去噪和估计。维纳滤波在时域和频域中都可以应用,是信号处理、图像处理等领域中的一种经典方法。
维纳滤波的核心思想是利用信号和噪声的统计特性,设计一个滤波器,使得滤波后的输出信号与期望信号之间的均方误差最小。算法逻辑可以分为四个步骤:
1.建模:
-
假设观测信号 x ( t ) x(t) x(t) 是真实信号 s ( t ) s(t) s(t)与噪声 n ( t ) n(t) n(t) 的叠加,即$ x(t)=s(t)+n(t)$。
-
假设噪声 n ( t ) n(t) n(t)是一个零均值的白噪声,且与信号 s ( t ) s(t) s(t) 互不相关。
2.频域表达:
- 将信号转换到频域,利用傅里叶变换,将维纳滤波器设计为频域滤波器。
3.维纳滤波器设计:
- 维纳滤波器的频域表达式为:
H ( f ) = S s ( f ) S s ( f ) + S n ( f ) H(f)=\frac{S_{s}(f)}{S_{s}(f)+S_{n}(f)} H(f)=Ss(f)+Sn(f)Ss(f)
其中, S s ( f ) S_{s}(f) Ss(f) 和 S n ( f ) S_{n}(f) Sn(f)分别是信号和噪声的功率谱密度。
4.应用滤波器:
- 对观测信号应用维纳滤波器,得到估计的真实信号。
频域维纳滤波
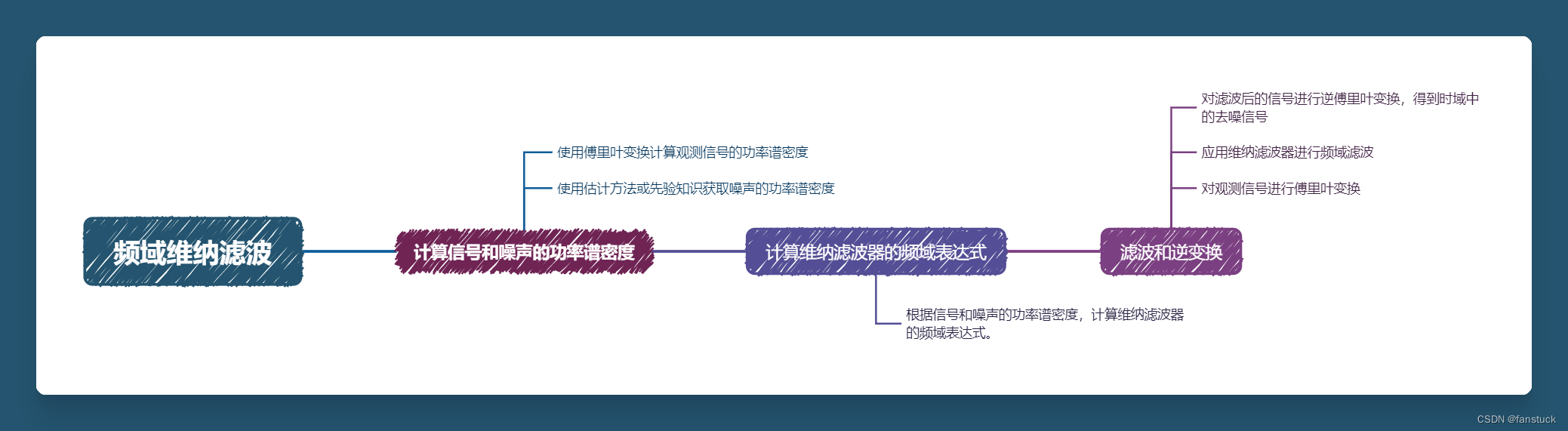
计算信号和噪声的功率谱密度:
- 使用傅里叶变换计算观测信号的功率谱密度。
- 使用估计方法或先验知识获取噪声的功率谱密度。
计算维纳滤波器的频域表达式:
- 根据信号和噪声的功率谱密度,计算维纳滤波器的频域表达式。
滤波和逆变换:
- 对观测信号进行傅里叶变换。
- 应用维纳滤波器进行频域滤波。
- 对滤波后的信号进行逆傅里叶变换,得到时域中的去噪信号。
def wiener_filter(noisy_signal, sample_rate, noise_power_spectrum): # 计算观测信号的功率谱密度 f, Pxx = scipy.signal.welch(noisy_signal, sample_rate, nperseg=1024) # 估计信号的功率谱密度(假设信号与噪声独立,且噪声功率谱密度已知) signal_power_spectrum = np.maximum(Pxx - noise_power_spectrum, 1e-8) # 计算维纳滤波器的频域表达式 H_wiener = signal_power_spectrum / (signal_power_spectrum + noise_power_spectrum) # 对观测信号进行傅里叶变换 noisy_signal_fft = np.fft.fft(noisy_signal) # 对维纳滤波器进行频域插值 H_wiener_interp = np.interp(np.fft.fftfreq(len(noisy_signal)), f, H_wiener) # 应用维纳滤波器进行频域滤波 filtered_signal_fft = noisy_signal_fft * H_wiener_interp # 对滤波后的信号进行逆傅里叶变换 filtered_signal = np.fft.ifft(filtered_signal_fft).real return filtered_signal
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
其中使用该算法前提条件需要计算出噪音的功率谱密度。噪声功率谱密度(Power Spectral Density, PSD)是描述噪声信号在频域中的能量分布的重要工具。在实际应用中,噪声功率谱密度通常需要根据观测到的噪声信号进行估计。我们可以通过自适应方法,通过统计分析或基于模型的方法估计噪声功率谱密度,适用于信号和噪声混合较复杂的情况。
def adaPtive_noisy(file,noise_estimation_duration=1.0): # 读取含噪信号音频文件 noisy_signal, sample_rate = sf.read(file) # 使用Welch方法计算含噪信号的功率谱密度 frequencies, Pxx = scipy.signal.welch(noisy_signal, sample_rate, nperseg=10000) # 估计噪声功率谱密度 noise_frames = int(noise_estimation_duration * sample_rate / 512) noise_power_spectrum = np.mean(Pxx[:noise_frames]) # 可视化噪声功率谱密度 plt.figure() plt.semilogy(frequencies, noise_power_spectrum) plt.title('Estimated Noise Power Spectral Density') plt.xlabel('Frequency [Hz]') plt.ylabel('Power Spectral Density [V^2/Hz]') plt.show() return noise_power_spectrum
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
那么音频各类去噪算法就先编码实现到此,后续我们可以根据不同的业务场景和需求来开展不同去噪效果的小型应用,而且也可以作为音视频直播或实现语音实时去噪效果。那么下一章节我们开始研究音频最为主要的特征以及对应含义,我们应该如何运用这些特征,如何通过特征来看透wav数据。



