- 1华为OD机试统一考试D卷C卷 - 可以组成网络的服务器(C++ Java JavaScript Python C语言)_华为od机试可以组成网络的服务器数
- 2java 牛客网之[动态规划 简单]NC1 子数组最大连续和_给定一个长度为 n 的数组,数组中的数为整数。请你选择一个非空连续子数组,使该子
- 3保研经验总结上篇_保研综合测评
- 43Dslicer_Editor(2)_3d slicer膨胀腐蚀
- 5华师计算机设计大赛,广东省首届高校大学生计算机设计大赛在华师举行
- 6redis 内存不足 排查_Redis连接问题排查与解决
- 7kali Linux 安装教程(保姆级)_kalilinux
- 8Python制作【大麦网】抢票程序,看演唱会再也不怕没票了_python抢票(1)_python自动抢票代码大麦
- 92024全国危险化学品经营单位安全管理人员在线模拟_某企业组织编制专项预案,因缺少人员
- 10A mapped type may not declare properties or methods in TS
K近邻法(KNN)
赞
踩
更多机器学习方法总结请到我这个博客链接
K近邻法(k-nearest neighbor,KNN)
1 K近邻定义
1、一句话定义:
给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的k个实例,这k个实例的多数属于某个类,就把该输入实例分为这个类。
2、三要素:距离度量,k值的选取,分类决策规则的选取。
- 距离度量一般采用欧氏距离,也可以是其他距离(Lp距离)
- k值选取将会对结果产生巨大的影响。如果k值较小,整体模型变的复杂,容易发生过拟合;如果k值过大,不相关的点也对预测产生影响,导致预测精度较低。一般可以采用交叉验证进行k值得选取。
- 分类决策规则:往往是多数表决。
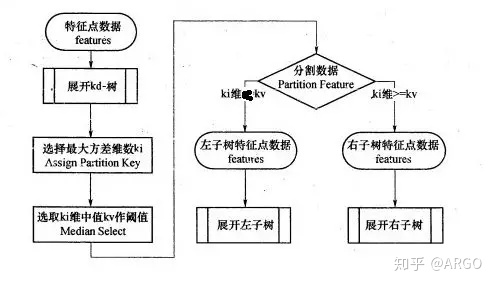
2 k近邻的实现-kd树
实现k近邻法时,主要考虑的问题是如何对训练数据进行快速k近邻搜索。这点在特征空间的维数大及训练数据容量大时尤其必要。最简单是的就是线性扫描,但对于高维数据不可取,因此采用特殊的存储结构kd树进行搜索。
2.1 kd树的构建
更多详情请见:kd树构建详解
kd树是二叉树,和分治法思想一样,利用已有数据进行空间切分。构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分,构成一系列的k维超矩形区域。kd树的每个结点对应于一个k维超矩形区域。
需要注意的是,每一刀都要切在数据点上面。主要考虑切分域和切分点的选择(分别使用方差最大优先和中位优先)
算法流程:
对于例子:构造一个平衡kd树。
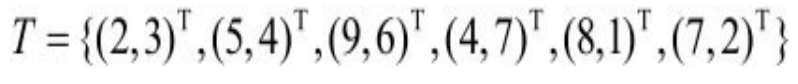
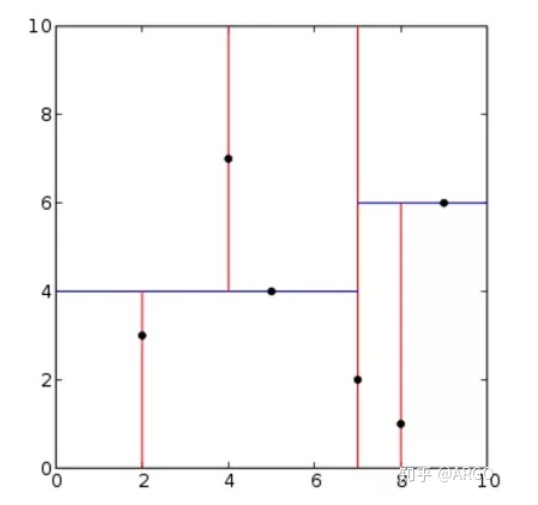
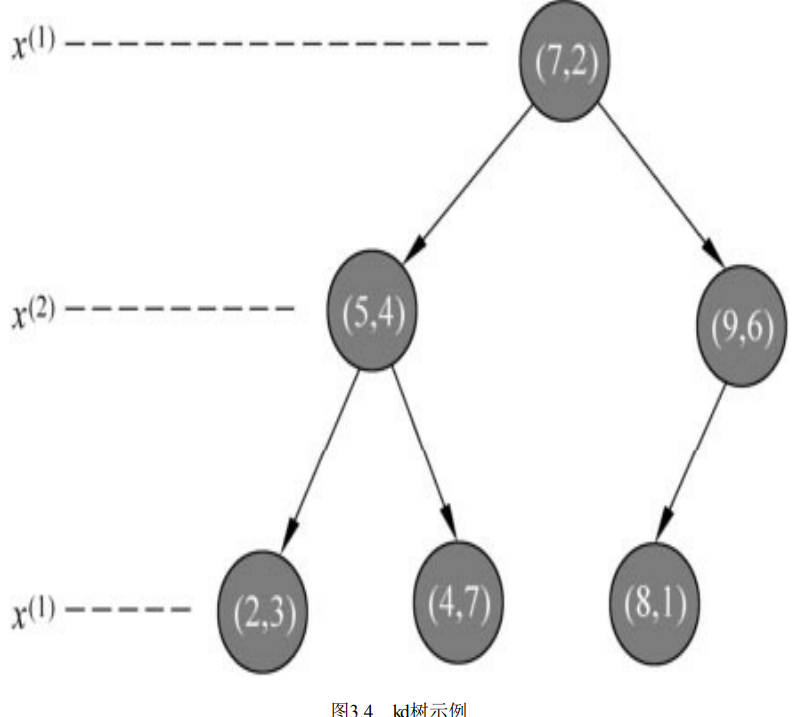
结果如下:
2.2 ball tree 和其他树类型介绍
在kd tree 中,我们看到一个导致性能下降的最核心因素是因为kd树的平面是一个个的方形,求最近邻时使用的是圆形。方形平面跟圆形相交的可能性是极高的,如果方形的交汇点多的话,圆形和几个平面相交的可能性就变得更大。这样,凡是相交的平面,都需要进行检查,大大的降低运行效率。
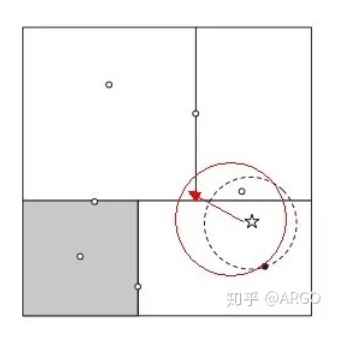
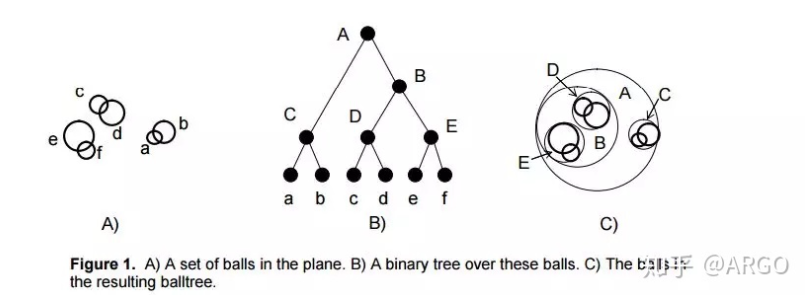
为了解决这一个问题,ball tree抛弃了kd树画的方形,而建立球形,去掉棱角。简而言之,就是使用超球面而不是超矩形划分区域。
3 搜索kd树
用目标数据在kd树中寻找最近邻时,最核心的两个部分是:
-
寻找近似点-寻找最近邻的叶子节点作为目标数据的近似最近点。
-
回溯-以目标数据和最近邻的近似点的距离沿树根部进行回溯和迭代。


