【计算机视觉】基础矩阵

---

一、外极几何

用两个相机在不同位置拍摄同一物体，两张照片中的景物有重叠部分，那么理论上这两张照片会存在一定的对应关系即外极几何。

外极几何示意图：

在上图中，PO₁O₂为极平面，O₁、O₂分别为相机的中心点，P为空间中一点，P在图像平面上的投影分别为p₁、p₂，照相机中心之间的基线O₁和O₂与图像平面交于外极点e₁、e₂。
而对极几何则是描述极点、极平面、极线这几个量之间的对应关系。

---

二、基础矩阵 F

1.基础矩阵原理

为了描述对极几何，引入基础矩阵F。对于一幅图像上的点x（图上p₁），在另一幅图像上存在对极线l’，并且在第二幅图像上，与x匹配的点x’（点p₂）必然在l’上。为了表示x与l’关系，我们令基础矩阵F定义为： l′=Fx。

假设第一幅图到第二幅图之间存在单应性变换H，则 x′=Hx。

又因为l’是表示过对极点e₂和图像点x’的直线，可以表示为： l′=e₂×x′=[e₂]xx′=[e₂]xHx。

所以可得 F=[e₂]xH。

其中e′=[a1,a2,a3]Te′=[a1,a2,a3]T，则它的反对称阵定义为：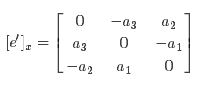

在已知两个摄像机的射影矩阵P和P’时，对于图像上的一点x，可以得到其反投影射线方程为： X(λ)=P⁺ x+λC

其中P⁺ 是P的伪逆，即PP⁺ = I，C为摄像机中心。射线上的两点：P⁺ x（当λ=0）、C（当λ=∞）在第二个摄像机P’拍摄下，在第二幅视图上的点分别为P′P⁺ 和P′C，这两点过对极线l’，即 l′=(P′C)×(P′P⁺ x)=[e′]_x(P′P⁺ )x

可以推得 F=[e′]_xP′P⁺

2.基础矩阵性质

（1） 基础矩阵是秩为2、自由度为7的齐次矩阵。
（2）若x与x’是两幅图上的对应点，那么x′^TFx=0。
（3）l’是对应于x的对极线，l′=Fx。
（4）若e是第二个摄像机光心在第一幅图像上的极点，那么Fe=0 。

3.基础矩阵估算方法

3.1 八点估算法

基本矩阵是由该方程定义的： x′^TFx=0

其中x↔x′是两幅图像的任意一对匹配点。由于每一组点的匹配提供了计算F系数的一个线性方程，当给定至少7个点（3×3的齐次矩阵减去一个尺度，以及一个秩为2的约束），方程就可以计算出未知的F。我们记点的坐标为x=(x,y,1)^T，x′=(x′,y′,1)^T

又因为F为：

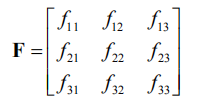
所以可得到方程：

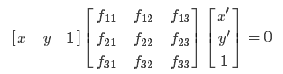
即相应方程式为

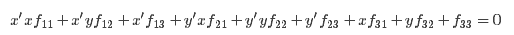
给定n组点的集合，我们有如下方程：

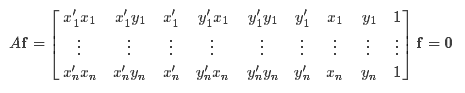
如果存在确定（非零）解，则系数矩阵A的秩最多是8。由于F是齐次矩阵，所以如果矩阵A的秩为8，则在差一个尺度因子的情况下解是唯一的。可以直接用线性算法解得。

如果由于点坐标存在噪声则矩阵AA的秩可能大于8（也就是等于9，由于A是n×9的矩阵）。这时候就需要求最小二乘解，这里就可以用SVD来求解，f的解就是系数矩阵A最小奇异值对应的奇异向量，也就是A奇异值分解后A=UDV^T中矩阵V的最后一列矢量，这是在解矢量f在约束∥f∥下取∥Af∥最小的解。以上算法是解基本矩阵的基本方法，称为8点算法。

上述求解后的F不一定能满足秩为2的约束，因此还要在F的基础上加以约束。通过SVD分解可以解决，令F=UΣV^T，则

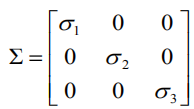
因为要秩为2，所以取最后一个元素设置为0，则

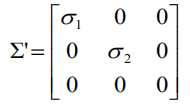
最终的解

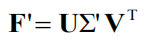
3.2 RANSAC随机取样一致法估算（略）

---

三、基础矩阵代码实现

1.相关代码

from PIL import Image
from numpy import *
from pylab import *
from PCV.geometry import camera
from PCV.geometry import homography
from PCV.geometry import sfm
from PCV.localdescriptors import sift
from PCV.tools import ransac
import numpy as np


# Read features
im1 = array(Image.open('pic1.jpg'))
sift.process_image('imim1.jpg', '
1
2
3
4
5
6
7
8
9
10
11
12
13