二分类支持向量机模型SVM知识点详解_基于svm(支持向量机)的二分类模型

1 引言

在本篇博客中，你将会了解到支持向量机分类器名字的由来、它的基本假设、支持向量机针对线性可分、广义线性、非线性情况下的解决方法以及一些具体的推导过程，支持向量机常见问题的解答。在本篇博客的第二部分会给一幅支持向量机整个过程的流程图，从图中你可以清晰的了解到支持向量机模型针对不同情况的的创建和求解过程，以及他们之间的关系，在图中涉及到的关键细节知识，会在第三部分给出详细的说明。因此，即使你之前没有接触过SVM，在你认真读了该篇博客也会有一个清晰的支持向量机建模框架。在本篇博客的最后将会给出支持向量机SVM从建模到求解整个过程的python实现代码及测试结果。废话不多说，开启你的学霸模式吧~

2 SVM全流程示意图

下图主要展示了，支持向量机构建时原问题，对偶问题及求解过程

2.1 图说三种分类情况
图一展示了线性可分情况，如图所示，图二展示了存在少量误分类点的线性可分情况，图三展示了非线性分类情况。

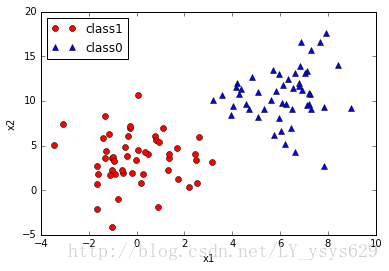
图1 线性可分情况

图2 线性不完全可分情况

图2非线性可分情况

2.2 7条说明详细解释SVM的关键知识点

• 说明1 –SVM的基本假设：
  

  ---

SVM模型是由少量几个样本点决定的，这几个样本点称为支持向量，支持向量距离超平面的距离是小于等于1的（原因后边有解释），假如SVM能够找出一个超平面或者超曲面使得支持向量能够尽可能的分类正确，且距离超平面或超曲面的距离尽可能的远，则非支持向量点，也能被正确分类且距离最远，该处距离的含义可认为分类正确的置信度，距离越远置信度越大。

• 说明2 –SVM的模型描述：

  ---

  SVM模型超平面描述为： $\pmb{w}*\pmb{x}+b=0$
  决策函数$f(x)=sign(\pmb{w}*\pmb{x}+b)$
  为什么说策略是间隔最大？接下来会给出答案。
  首先提一下两个概念：函数间隔和几何间隔（上述假设中的距离）
  函数间隔：$\hat{\gamma}_i=y_i(\pmb{w}*x_i+b)$
  几何间隔：$\gamma_i =\frac{\hat{\gamma}}{||\pmb{w}||}$
  （想象下点到线的距离,分类正确时，$y_i(\pmb{w}*x_i+b)=||\pmb{w}*x_i+b||$）
  假设，分类超平面已经确定，此时要找出距离超平面最短的样本点（支持向量点），可描述为：
  $\gamma=\min\limits_{i=1,2,...,n}\gamma_i=\min\limits_{i=1,2,...,n}\frac{\hat{\gamma}}{||\pmb{w}||}$
  根据假设，求该距离最大化时的超平面参数$\pmb{w},b$,描述为：
  $\max\limits_{\pmb{w},b} \gamma$等价于$\max\limits_{\pmb{w},b} \frac{\hat{\gamma}}{||\pmb{w}||}$
  

  $$\begin{equation} \begin{array}{lc} \qquad\qquad\max\limits_{\pmb{w},b} \frac{\hat{\gamma}}{||\pmb{w}||} & \\ s.t.\quad y_i(\pmb{w}*x_i+b) \ge \hat{\gamma} \qquad i=1,2,...,n, & \\ \end{array} \tag{1} \end{equation}$$
  由于$\hat{\gamma}$对求解优化问题无影响，因此可令其为1$\hat{\gamma}=1$证明如下：
  假设超平面参数为$\pmb{w}^*,b^*$,支持向量样本点为$(x_{min},y_{min})$,则支持向量的函数间隔为
  
  $$\begin{equation} \hat{\gamma}=y_{min}(\pmb{w}^*x_{min}+b^*)\tag{2} \end{equation}$$
  由于超平面同时缩放所有参数不会改变，所以令