强化学习算法原理总结---通俗易懂，入门最佳

        强化学习是一种机器学习方法，它涉及到智能系统在与环境互动的过程中，通过试错来学习最优的行为策略。在强化学习中，智能系统会根据当前的状态选择一个动作，然后观察环境的反馈（奖励或惩罚），并据此调整自己的策略，以便在未来获得更好的回报。

        强化学习在许多领域都有广泛的应用，包括自动驾驶、机器人控制、游戏设计等。它可以帮助智能系统在复杂、动态的环境中做出决策，并不断改进自己的表现。

---

        一下内容为近期学习强化学习后简单总结的一些原理，希望可以对入门强化学习的伙伴有所帮助，如有总结不到位地方欢迎指正！

---

目录

马尔科夫链

马尔科夫链包含三要素

马尔科夫链的不确定性

核心思想

Q值和V值

Q值和V值计算

Q到V

V到Q

蒙地卡罗方法（Monte-Carlo）估算V值

计算流程

G的意义

V和G的关系

时序差分TD估算V值

Q-learning算法

算法流程

DQN算法

算法流程

策略梯度（Policy Gradient）算法

PG深度强化学习算法与Q系列算法相比

优势主要有

缺点主要有

Actor-Critic算法

TD-error

算法流程

DDPG-深度确定性策略梯度算法

流程

DDPG 4个网络的功能定位

Critic

Actor

TD3-双延迟深度确定性策略梯度算法

基本思路

基本结构

TD3对DDPG的优化

---

---

马尔科夫链

马尔科夫链是用来描述智能体和环境互动的过程。

马尔科夫链包含三要素

state，action，reward。

state：只有智能体能够观察到的才是state。

action：智能体的动作。

reward：引导智能体工作学习的主观的值。

马尔科夫链的不确定性

不确定性在马尔科夫链中主要体现在以下几个方面：

初始状态的不确定性：在马尔科夫链中，初始状态是随机确定的。也就是说，在开始时，并不能确定系统处于哪个特定的状态。

转移概率的不确定性：马尔科夫链的状态转移是根据转移概率进行的。转移概率表示系统从一个状态转移到另一个状态的概率。这些转移概率通常是事先给定的，但在某些情况下可能是未知的或模糊的。

长期状态的不确定性：马尔科夫链的长期行为是由初始状态和状态转移概率共同决定的。对于有限状态空间的马尔科夫链，经过足够长时间后，系统将收敛到一个稳定的状态分布。然而，在某些情况下，系统可能无法达到平稳状态，或者平稳状态可能是多个状态的混合。

核心思想

如果你不希望孩子有某种行为，那么当这种行为出现的时候就进行惩罚。如果你希望孩子坚持某种行为，那么就进行奖励。这也是整个强化学习的核心思想。

Q值和V值

评估动作的价值，称为Q值：它代表了智能体选择这个动作后，一直到最终状态奖励总和的期望；

假设现在需要求某状态S的V值，那么我们可以这样：

1、我们从S点出发，并影分身出若干个自己;

2、每个分身按照当前的策略选择行为;

3、每个分身一直走到最终状态，并计算一路上获得的所有奖励总和;

4、我们计算每个影分身获得的平均值,这个平均值就是我们要求的V值。

评估状态的价值，称为V值：它代表了智能体在这个状态下，一直到最终状态的奖励总和的期望。

假设现在我们需要计算，某个状态S下的一个动作A的Q值：

1、我们就可以从A这个节点出发，使用影分身之术；

2、每个影分身走到最终状态,并记录所获得的奖励；

3、求取所有影分身获得奖励的平均值，这个平均值就是我们需要求的Q值。

价值越高，表示我从当前状态到最终状态能获得的平均奖励将会越高。因为智能体的目标数是获取尽可能多的奖励，所以智能体在当前状态，只需要选择价值高的动作就可以了。

Q值和V值计算

Q到V

一个状态的V值，就是这个状态下的所有动作的Q值，在策略下的期望。

vπs=a∈Aπasqπs，a

V到Q

Q就是V的期望！而且这里不需要关注策略，这里是环境的状态转移概率决定的。

qπs，a=Rsa+γs`Pss`avπs`

其中Pss`a是状态转移概率；γ是折扣率；Rsa是奖励。

蒙地卡罗方法（Monte-Carlo）估算V值

计算流程

1、把智能体放到环境的任意状态；

2、从这个状态开始按照策略进行选择动作，并进入新的状态。

3、重复步骤2，直到最终状态；

4、我们从最终状态开始向前回溯：计算每个状态的G值。

5、重复1-4多次，然后平均每个状态的G值，这就是我们需要求的V值。

G的意义

在某个路径上，状态S到最终状态的总收获。

V和G的关系

V是G的平均数。

时序差分TD估算V值

在MC，G是更新目标，而在TD，我们只不过把更新目标从G，改成r+gamma*V

用更可靠的估计取代现有估计，V（St）是现有估计，r+ gamma*V（St+1）是更可靠估计，因为其中多了真实值r，所以不断用更可靠估计取代现有估计，就能慢慢接近真实值。

Q-learning算法

算法流程

1、在任意的state出发

2、用noisy-greedy的策略选定动作A；

3、在完成动作后，我们将会进入新状态St+1；

4、检查St+1中所有动作，看看哪个动作的Q值最大；

5、用以下的公式更新当前动作A的Q值；

6、继续从s'出发，进行下一步更新 1-6步我们作为一个EP，进行N个EP的迭代。

DQN算法

Deep network + Qlearning = DQN

算法流程

1、初始化一个网络，用于计算Q值。（在Qlearning，我们用Qtable）

3、我们开始一场游戏。

4、随机从一个状态s开始。

5、我们把s输入到Q，计算s状态下，a的Q值 Q（s）

6、我们选择能得到最大Q值的动作，a

7、我们把a输入到环境，获得新状态s’，r，done

8、计算目标 y = r + gamma * maxQ(s')

9、训练Q网络，缩小Q（s，a）和y 的大小

10、开始新一步，不断更新

假设我们需要更新当前状态St下的某动作A的Q值：Q(S,A)，我们可以这样做：

1、执行A，往前一步，到达St+1;

3、把St+1输入Q网络，计算St+1下所有动作的Q值；

4、获得最大的Q值加上奖励R作为更新目标；

5、计算损失 - Q(S,A)相当于有监督学习中的logits - maxQ(St+1) + R 相当于有监督学习中的lables - 用mse函数，得出两者的loss

6、用loss更新Q网络。

也就是，我们用Q网络估算出来的两个相邻状态的Q值，他们之间的距离，就是一个r的距离。

策略梯度（Policy Gradient）算法

DQN是一个TD+神经网络的算法，PG是一个蒙地卡罗+神经网络的算法。

如果动作使得最终回报变大，那么增加这个动作出现的概率，反之，减少这个动作出现的概率

PG深度强化学习算法与Q系列算法相比

优势主要有

1、可以处理连续动作空间或者高维离散动作空间的问题。

2、容易收敛，在学习过程中，策略梯度法每次更新策略函数时，参数只发生细微的变化，但参数的变化是朝着正确的方向进行迭代，使得算法有更好的收敛性。而价值函数在学习的后期，参数会围绕着最优值附近持续小幅度地波动，导致算法难以收敛。

缺点主要有

1、容易收敛到局部最优解，而非全局最优解；

2、策略学习效率低；

3、方差较高：这个可谓是普通PG深度强化学习算法最不可忍受的缺点了，由于PG算法参数更新幅度较小，导致神经网络有很大的随机性，在探索过程中会产生较多的无效尝试。另外，在处理回合结束才奖励的问题时，会出现不一致的问题：回合开始时，同样的状态下，采取同样的动作，但是由于后期采取动作不同，导致奖励值不同，从而导致神经网络参数来回变化，最终导致Loss函数的方差较大。

Actor-Critic算法

Actor-Critic，用了两个网络，两个网络有一个共同点，输入状态S:

一个输出策略，负责选择动作，我们把这个网络成为Actor；

一个负责计算每个动作的分数，我们把这个网络成为Critic。

Actor是舞台上的舞者，Critic是台下的评委：

Actor在台上跳舞，一开始舞姿并不好看，Critic根据Actor的舞姿打分。Actor通过Critic给出的分数，去学习：如果Critic给的分数高，那么Actor会调整这个动作的输出概率；相反，如果Critic给的分数低，那么就减少这个动作输出的概率。

在DQN预估的是Q值，在AC中的Critic，估算的是V值，而Q值的期望(均值)就是V。

TD-error

1、为了避免正数陷阱，希望Actor的更新权重有正有负。因此，我们把V值减去他们的均值Q。有：V(s)-Q(s,a)

2. 为了避免需要预估V值和Q值，我们希望把Q和V统一；由于：

Q(s,a) = gamma * V(s') + r。

所以我们得到TD-error公式：

TD-error = V(s) - gamma * V(s') + r

3. TD-error就是Actor更新策略时候，带权重更新中的权重值；

4. 现在Critic不再需要预估Q，而是预估V。TD-error就是Critic网络需要的loss，Critic函数需要最小化TD-error。

算法流程

1、定义两个network：Actor 和 Critic；

2、进行N次更新。

1）从状态s开始，执行动作a，得到奖励r，进入状态s'；

2）记录的数据；

3）把输入到Critic，根据公式：TD-error = gamma * V(s') + r - V(s) 求TD-error，并缩小TD-error；

4）把输入到Actor，计算策略分布。

DDPG-深度确定性策略梯度算法

流程

DDPG 4个网络的功能定位

1、Actor当前网络：根据当前状态S输出动作A，并用动作A操作环境，生成下一状态S’以及奖励R；更新网络参数θ；

2、Actor目标网络：根据下一状态S’输出下一动作A’，并定期将当前网络的参数θ复制更新目标网络的θ’；

3、Critic当前网络：根据状态S和动作A计算当前网络Q值Q(S,A,w)；更新网络参数w；

4、Critic目标网络：根据状态S’和动作A’计算目标网络Q值中的Q’(S’,A’,w’)部分（目标网络Q值记作yi，且yi=R+γ*Q’(S’,A’,w’)）；定期将critic当前网络中的参数w复制更新目标网络的参数w’。

Critic

1、Critic网络的作用是预估Q，和AC中的Critic不一样，这里预估的是Q不是V；

2、Critic的输入有两个：动作和状态，需要一起输入到Critic中；

3、Critic网络的loss和AC一样，用的是TD-error。

Actor

1、和AC不同，Actor输出的是一个动作；

2、Actor的功能是，输出一个动作A，这个动作A输入到Crititc，能够获得最大的Q值。

3、Actor的更新方式和AC不同，不是用带权重梯度更新，而是用梯度上升。

TD3-双延迟深度确定性策略梯度算法

DDPG源于DQN，是DQN解决连续控制问题的一种方法。然而DQN存在过估计问题。

过估计是指估计的值函数比真实的值函数大。因为DQN是一种off-policy的方法，每次学习时，不是使用下一次交互的真实动作，而是使用当前认为价值最大的动作来更新目标值函数，所以会出现对Q值的过高估计。通过基于函数逼近方法的值函数更新公式可以看出：

解决办法：Double Q Learning方法，例如应用到DQN中，就是Double DQN，即DDQN。

Double Q Learning是将动作的选择和动作的评估分别用不同的值函数来实现：

1、动作的选择：

2、动作的评估：选出a`后，利用a`处的动作值函数构造TD目标，TD目标公式为：

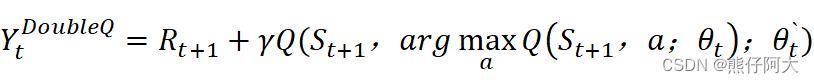
基本思路

过估计这个问题也会出现在DDPG中，在TD3中，使用两套网络(Twin)表示不同的Q值，通过选取最小的那个作为我们更新的目标（Target Q Value），抑制持续地过高估计。

基本结构

DDPG算法涉及了4个网络，所以TD3需要用到6个网络。

目标网络Q1(A')和Q2(A')取最小值min(Q1,Q2)，代替了DDPG的Q'(A')计算更新目标，即：

Ytarget = r + gamma * min(Q1, Q2)，Ytarget将作为Q1和Q2两个网络的更新目标。

TD3对DDPG的优化

主要有以下三点

1、用类似Double DQN的方式，解决了DDPG中Critic对动作Q值过估计的问题；

2、延迟Actor更新，使Actor的训练更加稳定；

3、在Actor目标网络输出动作A’加上噪声，增加算法稳定性。