刷题之动态规划-路径问题

前言

大家好，我是jiantaoyab，开始刷动态规划的题目了，要特别注意初始化的时候给什么值。

动态规划5个步骤

1. 状态表示 ：dp数组中每一个下标对应值的含义是什么->dp[i]表示什么
2. 状态转移方程： dp[i] 等于什么
3. 1 和 2 是动态规划的核心步骤，第三步是初始化，保证填表的时候不越界
4. 填表顺序：为了保证填写当前状态的时候，所需要的状态已经计算过
5. 返回值

第 N 个泰波那契数

题目分析

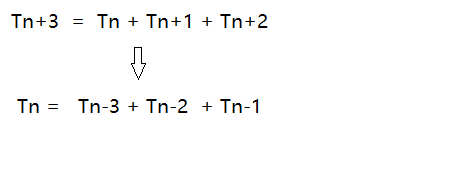
我们用动态规划来解决

1. dp[i] : 表示第i个泰波那契数
2. dp[i] = dp[i - 3] + dp[i - 2] + dp [i - 1]
3. 初始化： dp[0] = 0; dp[1] = 1 ; dp[2] = 1;
4. 填表顺序：从左道右
5. 返回值：dp[n]

代码

class Solution {
public:
    int tribonacci(int n) {
      if(n == 0) return 0;
      if(n == 1 || n == 2) return 1;
      int dp[1000] = {0};
      dp[0] = 0, dp[1] = 1, dp[2] = 1;
      for(int i = 3; i <= n; i++)
      {
        dp[i] = dp[i-3] + dp[i-2] + dp[i-1];
      }
      return dp[n];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

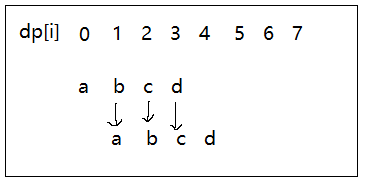
优化一下，可以看到只需要三个变量也能完成这个操作。

class Solution {
public:
    int tribonacci(int n) {
      if(n == 0) return 0;
      if(n == 1 || n == 2) return 1;
      int a = 0, b = 1, c = 1, d = 0;
      for(int i = 3; i <= n; i++)
      {
        d = a + b + c;
        a = b;
        b = c;
        c = d;
      }
      return d;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

三步问题

题目分析

1. dp[i] :表示去到当前台阶有几种方法
2. dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
3. 初始化 dp[1] = 1; dp[2] = 2; dp[3] = 4;
4. 填表顺序从左到右
5. 返回值 d[n]

代码

class Solution {
public:
    int waysToStep(int n) {
      vector<int>dp(n + 1);
      if(n == 1 || n == 2) return n;
      if(n == 3) return 4;
      const int MOD = 1000000007;
      dp[1] = 1; dp[2] = 2; dp[3] = 4;
      for(int i = 4; i <= n; i++)
      {
        dp[i] = ((dp[i-3] + dp[i-2]) % MOD + dp[i-1]) % MOD;
      }
      return dp[n];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

使用最小花费爬楼梯

题目分析

1. dp[i]：到达 i位置的最小花费
2. dp[i] = min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2]);
3. 初始化：dp[0] = dp[1] = 0;
4. 填表顺序:从左到右
5. 返回值：dp[n]

代码

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
      int n = cost.size();
      vector<int> dp(n + 1);
      dp[0] = dp[1] = 0;
      for(int i = 2; i <= n; i++)
      {
        dp[i] = min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2]);
      }
      return dp[n];
      
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

解码方法

题目分析

1. dp[i]：是表示是 i 位置为结尾的解码方法总数
2. dp[i] = dp[i - 1] + dp [i - 2];
3. 初始化：dp[0] = 0 / 1 dp[1] = 0/ 1/ 2
4. 填表顺序:从左到右
5. 返回值：dp[n - 1]

代码

class Solution {
public:
    int numDecodings(string s) {
      int n = s.size();
      vector<int> dp (n);
      
      //初始化
      dp[0] = s[0] != '0';
      if(n == 1) return dp[0];
      if(s[0] != '0' && s[1] != '0') dp[1] += 1;
      int tmp = (s[0] - '0') * 10 + (s[1] - '0');
      if(tmp >= 10 && tmp <= 26) dp[1] += 1;
      
      //处理剩下的
     for(int i = 2; i < n; i++)
     {
      //单独一个字符
        if(s[i] != '0') dp[i] += dp[i - 1];
      //2个字符
        int tmp = (s[i - 1] - '0') * 10 + (s[i] - '0');
        if(tmp >= 10 && tmp <= 26) dp[i] += dp[i - 2];
     }
      return dp[n - 1];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

优化代码

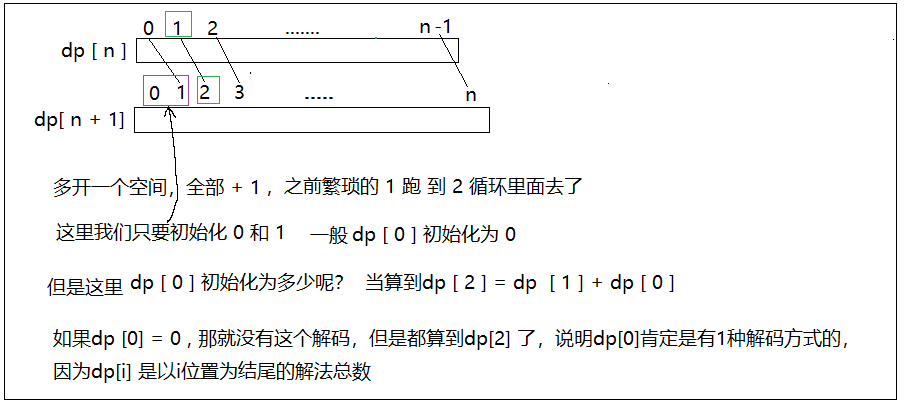
class Solution {
public:
    int numDecodings(string s) {
      int n = s.size();
      vector<int> dp (n + 1); 
      //初始化
      dp[0] = 1;
      dp[1] = s[1 - 1] != '0';  
      //处理剩下的
     for(int i = 2; i <= n; i++)
     {
      //单独一个字符
        if(s[i - 1] != '0') dp[i] += dp[i - 1];
      //2个字符
        int tmp = (s[i - 2] - '0') * 10 + (s[i - 1] - '0');
        if(tmp >= 10 && tmp <= 26) dp[i] += dp[i - 2];
     }
      return dp[n];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

不同路径

题目分析

1. dp[i] [j]：走到 i,j 位置有多少种方式
2. dp[i] [j] = dp[i] [j - 1] + dp[i - 1] [j];
3. 初始化：新增加一列和一行
4. 填表顺序:从上到下，左到右填表
5. 返回值：dp[m] [n]

代码

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m+1, vector<int>(n+1));
        //初始化
        dp[0][1] = 1;
        for(int i = 1; i <= m; i++)
        {
          for(int j = 1; j <= n; j++)
          {
            dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
          }
        }
        return dp[m][n];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

不同路径 II

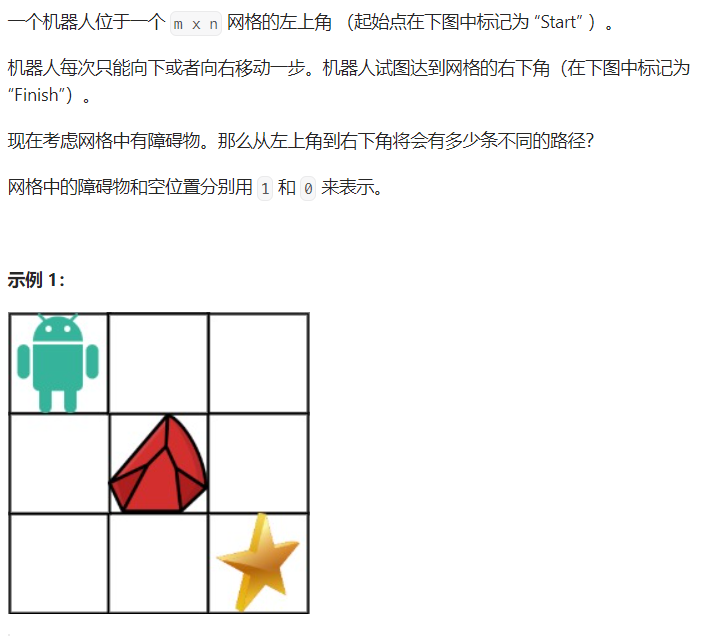
题目分析

1. dp [i] [j] : 到达i,j这个位置有多少种方法
2. dp [i] [j] = dp[i - 1] [j] + dp [i] [j - 1]
3. 初始化：dp[1] [0] = 1;
4. 填表顺序：从上到下，从左到右
5. 返回值： dp[m] [n]

代码

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
          int m = obstacleGrid.size(), n = obstacleGrid[0].size();
          vector<vector<int>> dp(m + 1, vector<int>(n + 1));
          //初始化
          dp[1][0] = 1;
          for(int i = 1; i <= m; i++)
          {
            for(int j = 1; j <= n; j++)
            {
              if(obstacleGrid[i - 1][j - 1] != 1)
              dp[i][j] = dp[i - 1][j] + dp[i][j -1];
            }

          }
          return dp[m][n];
    } 
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

珠宝的最高价值

题目分析

1. dp [i] [j] : 到达i,j这个位置的最高价值
2. dp [i] [j] =max(dp[i-1] [j], dp[i] [j-1]) + frame[i-1] [j-1];
3. 初始化：默认都是0不用初始化
4. 填表顺序：从上到下，从左到右
5. 返回值： dp[m] [n]

代码

class Solution {
public:
    int jewelleryValue(vector<vector<int>>& frame) {
        int m = frame.size(), n = frame[0].size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1));
        for(int i = 1; i <= m; i++)
          for(int j = 1; j <= n; j++)
          {           
            dp[i][j] =  max(dp[i-1][j], dp[i][j-1]) + frame[i-1][j-1];
          }
        return dp[m][n];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13

下降路径最小和

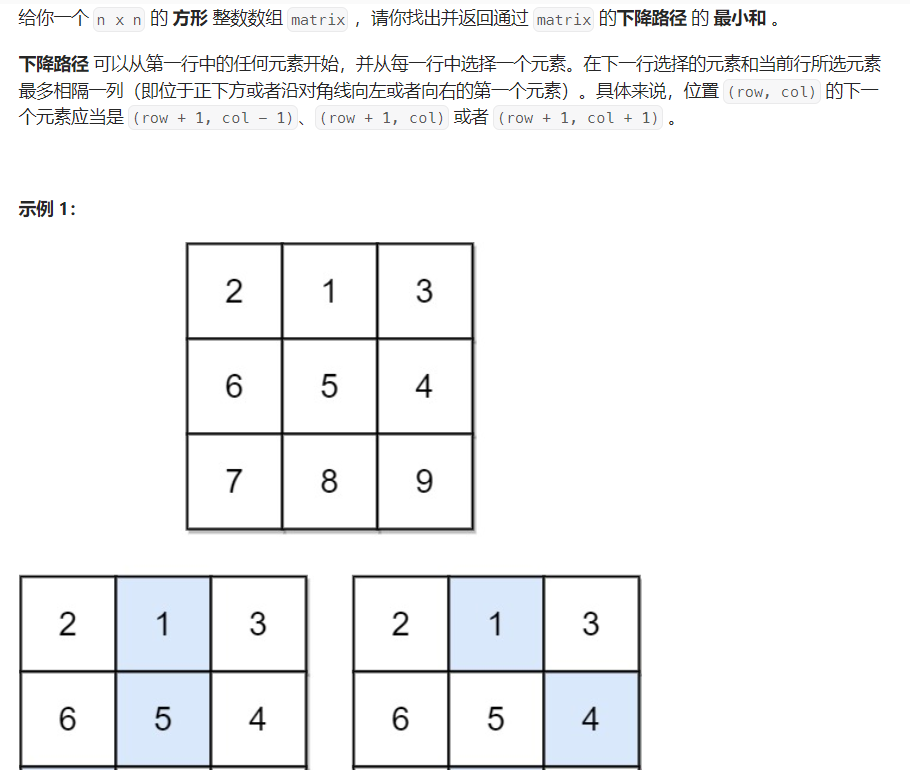
题目分析

1. dp[i] [j] : 到达i,j位置的最小下路径
2. dp[i] [j] : min(dp[i+1] [j-1], dp[i+1] [j+1], dp[i+1] [j]) + matrix[i-1] [j - 1]
3. 初始化：多给1行 和2列
4. 填表顺序：从上到下，从左到右
5. 返回值： 最后一行的最小值

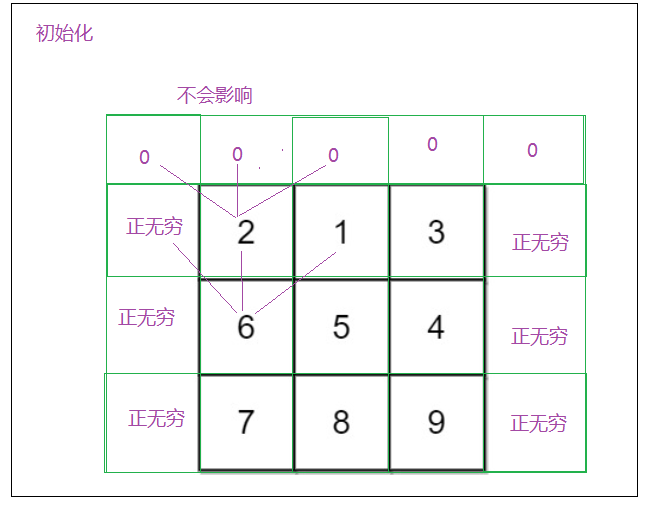
代码

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& matrix) {
     int n = matrix.size();
     vector<vector<int>> dp(n + 1, vector<int>(n + 2, INT_MAX));
      for(int j = 0; j < n + 2; j++) dp[0][j] = 0;
      for(int i = 1; i <= n; i++)
      {
         for(int j = 1; j <= n; j++)
        {
          dp[i][j] = min(min(dp[i-1][j-1], dp[i-1][j]), dp[i-1][j+1]) + matrix[i-1][j-1];
        }
      
      }      
      //返回值
      int ret = INT_MAX;
      for(int j = 1; j <= n; j++)
      {
        ret = min(ret, dp[n][j]);
      }
      return ret;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

最小路径和

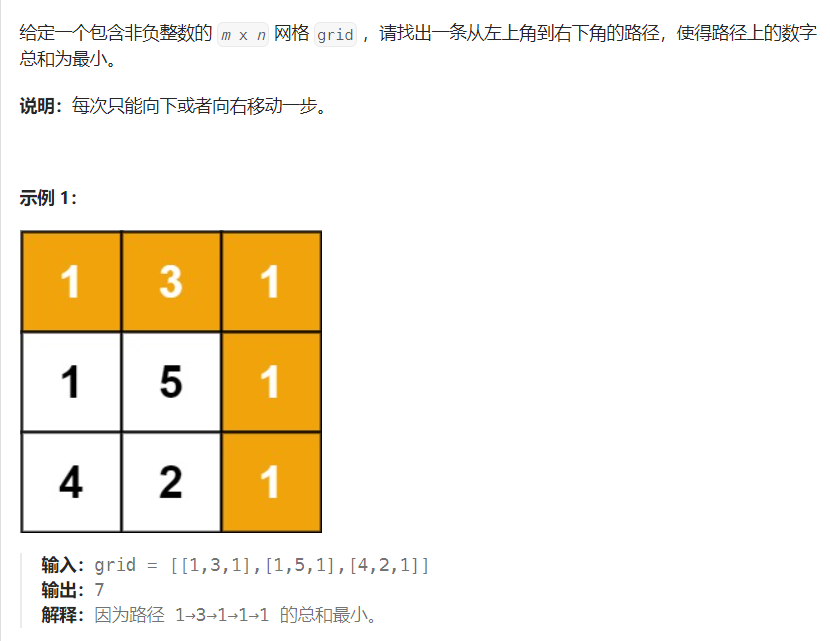
代码

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));
        dp[1][0] = dp[0][1] = 0; 
        for(int i = 1; i <= m; i++)
          for(int j = 1; j <= n; j++)
          {
            dp[i][j] = min(dp[i][j - 1], dp[i - 1][j]) + grid[i - 1][j - 1];
          }
        
      return dp[m][n];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

地下城游戏（反着来）

题目分析

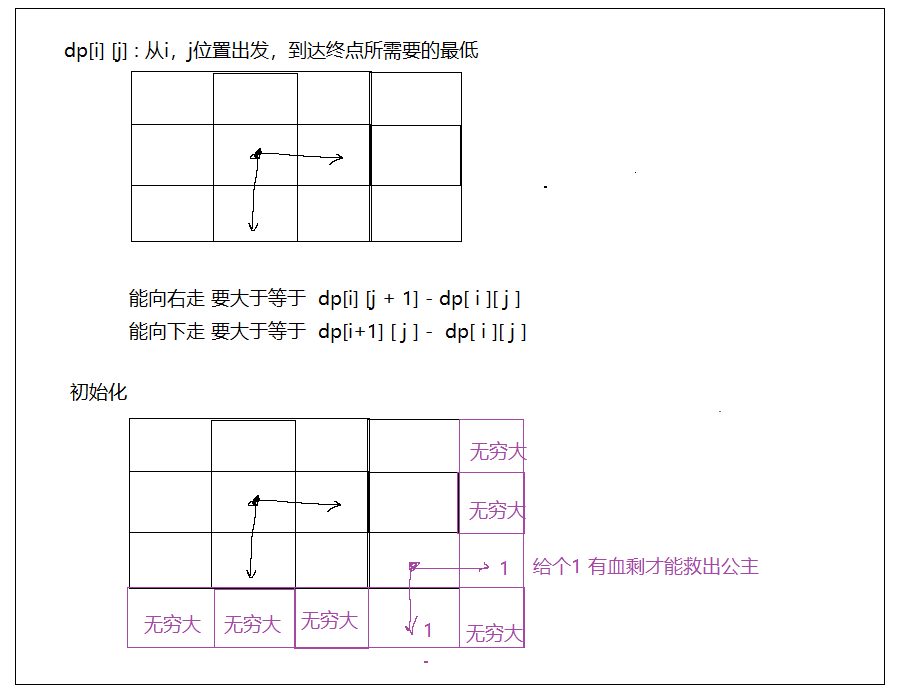
1. dp[i] [j] : 从i，j位置出发，到达终点所需要的最低

2. dp[i] [j] = min(dp[i] [j + 1], dp[i + 1] [j]) - dungeon[i] [j];

3. 初始化 dp[m +1] [n -1] = dp [m - 1] [n + 1] = 1;

4. 填表顺序：从下到上，从右到左

5. 返回值： dp[0] [0]

代码

class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) {
      int m = dungeon.size(), n = dungeon[0].size();
      vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));
      //初始化
      dp[m][n -1] = dp [m - 1][n] = 1;
      for(int i = m - 1; i >= 0; i--)
        for(int j = n - 1; j >= 0; j--)
        {
          dp[i][j] = min(dp[i][j + 1], dp[i + 1][j]) - dungeon[i][j];
          dp[i][j] = max(1, dp[i][j]); //如果血包很大，会出现负数，这里取1就是最低血
          
        }
        return dp[0][0];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17