- 1直接拿来用!最火的Android开源项目(三)(完结篇)_求android 简单项目所有完整源代码,要能够直接导入adt中使用的
- 2西红柿叶病害检测(yolov8模型,从图像、视频和摄像头三种路径识别检测,包含登陆页面、注册页面和检测页面)
- 3数据结构与算法导论---通讯录的实现_数据结构与算法实训通讯录代码总结
- 4vivo刷入鸿蒙,vivo鸿蒙系统刷机包
- 5非技术面试题_java非技术面试题
- 6100天精通Go语言(精品VIP版)专栏简介
- 7区块链的前世今生:走向高可靠企业应用
- 8动态规划之背包问题(java)全面总结_java 背包问题解析
- 9如何解决由于动态数据导致el-select下拉组件无法回显数据的问题_el-select动态添加的options如何回显
- 10玩转Mysql 五(MySQL索引)
数字图像处理学习——(一)双线性差值算法
赞
踩
一、线性差值
直接看图

若已知图中两点A(x0,y0),B(x1,y1),和该直线上任意一点P的横坐标x,求P该直线上的一点的纵坐标。
很容易可以得到,根据直线的定理。
(
y
−
y
0
)
/
(
x
−
x
0
)
=
(
y
1
−
y
0
)
/
(
x
1
−
x
0
)
(y-y0)/(x-x0)=(y1-y0)/(x1-x0)
(y−y0)/(x−x0)=(y1−y0)/(x1−x0);
得:
y
=
(
x
1
−
x
)
/
(
x
1
−
x
0
)
y
0
+
(
x
−
x
0
)
/
(
x
1
−
x
0
)
y
1
y=(x1-x)/(x1-x0)y0+(x-x0)/(x1-x0)y1
y=(x1−x)/(x1−x0)y0+(x−x0)/(x1−x0)y1;
x1,x0,y1,y0为定值,可将上式变换为:
y
(
x
1
−
x
0
)
=
(
x
1
−
x
)
y
0
+
(
x
−
x
0
)
y
1
y(x1-x0)=(x1-x)y0+(x-x0)y1
y(x1−x0)=(x1−x)y0+(x−x0)y1
可以看出P点的值受A,B两点影响,离的越近,影响越大。在公式中表现为离得越近乘的权值越大。
二、双线性差值
理解了线性差值,双线性差值就很容易理解了。
双线性差值可以视作线性差值的升维,也就是说在两个方向分别作线性差值。
以上图为例
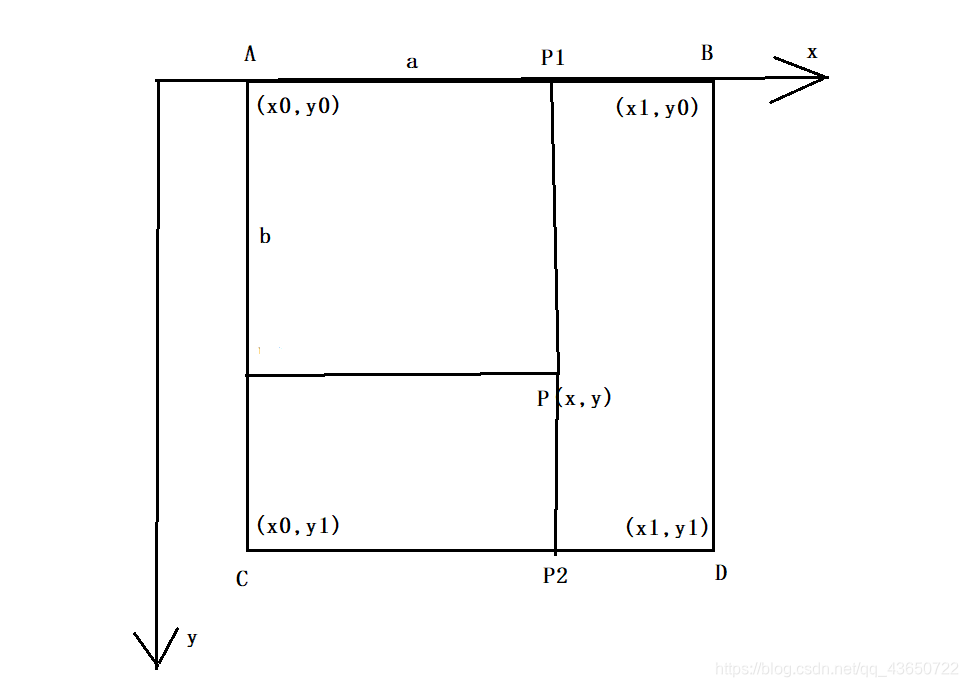
P的值可视作P1与P2的线性差值,而P1又可视作A,B的线性差值,P2可视作C,D的线性差值。
P
1
(
x
1
−
x
0
)
=
A
(
x
1
−
x
)
+
B
(
x
−
x
0
)
P1(x1-x0)=A(x1-x)+B(x-x0)
P1(x1−x0)=A(x1−x)+B(x−x0);
P
2
(
x
1
−
x
0
)
=
C
(
x
1
−
x
)
+
D
(
x
−
x
0
)
P2(x1-x0)=C(x1-x)+D(x-x0)
P2(x1−x0)=C(x1−x)+D(x−x0);
若设
a
=
(
x
−
x
0
)
/
(
x
1
−
x
0
)
a=(x-x0)/(x1-x0)
a=(x−x0)/(x1−x0);
b
=
(
y
−
y
0
)
/
(
y
1
−
y
0
)
b=(y-y0)/(y1-y0)
b=(y−y0)/(y1−y0);
则上式可变为:
P
1
=
A
(
1
−
a
)
+
B
∗
a
P1=A(1-a)+B*a
P1=A(1−a)+B∗a;
P
2
=
C
(
1
−
a
)
+
D
∗
a
P2=C(1-a)+D*a
P2=C(1−a)+D∗a;
P可视作P1与P2的线性差值
则:
P
=
P
1
(
1
−
b
)
+
P
2
∗
b
P=P1(1-b)+P2*b
P=P1(1−b)+P2∗b
将P1,P2带入可得
P
=
A
(
1
−
a
)
(
1
−
b
)
+
B
∗
a
(
1
−
b
)
+
C
(
1
−
a
)
b
+
D
∗
a
∗
b
P=A(1-a)(1-b)+B*a(1-b)+C(1-a)b+D*a*b
P=A(1−a)(1−b)+B∗a(1−b)+C(1−a)b+D∗a∗b
同样符合距离越近权重越大的原则


