线性插值 多项式插值 样条插值 牛顿插值总结_已知x大于等于0小于等于10,算y=sinx的线性样条插值

项目github地址：bitcarmanlee easy-algorithm-interview-and-practice
欢迎大家star，留言，一起学习进步

1.什么是插值

在数值分析中，插值(interpolation)是一种通过已知的、离散的数据点，在范围内推求新数据点的过程或方法。求解科学和工程的问题时，通常有许多数据点借由采样、实验等方法获得，这些数据可能代表了有限个数值函数，其中自变量的值。而根据这些数据，我们往往希望得到一个连续的函数（也就是曲线）；或者更密集的离散方程与已知数据互相吻合，这个过程叫做拟合。
与插值密切相关的另一个问题是通过简单函数逼近复杂函数。假设给定函数的公式是已知的，但是太复杂以至于不能有效地进行评估。来自原始函数的一些已知数据点，或许会使用较简单的函数来产生插值。当然，若使用一个简单的函数来估计原始数据点时，通常会出现插值误差；然而，取决于该问题领域和所使用的插值方法，以简单函数推得的插值数据，可能会比所导致的精度损失更大。

举个简单的例子，已知数据:
$$\begin{gathered} x_1=1,y_1=2 \\ {x}_2=2,y_2=3 \\ {x}_3=4,y_3=6 \end{gathered}$$
求$x=3$时y的值是多少？

2.示例

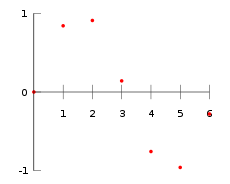
上图为数据点在x,y平面的显示图

插值就是提供了一些算法估算中间点函数的值。比如当x=2.5时，f(x)=?
有许多不同的插值方法，其中一些在下面描述。 在选择适当的算法时需要考虑的一些问题是：方法有多准确？ 它的计算成本有多高？ 插值有多平滑？ 需要多少数据点？

3.片段插值，最近邻插值

最简单的插值方法是找到最近的数据值，并分配相同的值。这种方法又称为最近邻插值。在简单的问题中，不太可能使用这种方法，因为线性插值几乎一样容易，但在高维度的多变量插值中，这可能是衡量速度和简单性的有利选择。

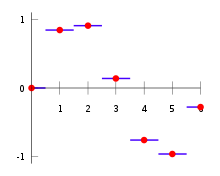
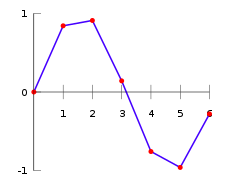
4.线性插值

假设我们已知坐标$(x_0,y_0),(x_1,y_1)$，当要求$[x_0,x_1]$区间内任一位置x在该条直线上的值时，由初中数学知识我们就可以求解:
$$\frac{y-y_0}{x-x_0}=\frac{y_1-y_0}{x_1-x_0}$$
因为x值已知，从上面的公式很容易求得y的值。

线性插值经常用于已知函数 f 在两点的值要近似获得其它点数值的方法，这种近似方法的误差定义为
$$R_T=f(x)-p(x)$$
其中$p(x)$表示上面定义的线性插值多项式。
根据罗尔定理，可以证明:如果f(x)有二阶连续导数，那么误差范围为：

$$|R_T|\le \frac{(x_1-x_0{)}^2}{8}\underset{x_0\le x\le x_1}{\max }|f^{\prime \prime }(x)|$$

正如所看到的，函数上两点之间的近似随着所近似的函数的二阶导数的增大而逐渐变差。从直观上来看也是这样：函数的曲率越大，简单线性插值近似的误差也越大。

5.多项式插值

多项式插值是线性插值的推广。线性插值是一个线性函数，我们现在用一个更高阶的多项式代替这个插值。 再考虑一下上面给出的问题。以下的六次多项式经历了所有七个点：
$$f(x)=-0.0001521x^6-0.003130x^5+0.07321x^4-0.3577x^3+0.2255x^2+0.9038x$$

如果将x=2.5带入，有f(2.5)=0.5965。一般情况下，如果我们有n个数据点，那么在所有的数据点中只有一个最多n-1次多项式可以完美拟合。此外，插值是一个多项式，因此是无限可微的。所以我们看到多项式插值克服了线性插值的大部分问题。但是，多项式插值也有一些缺点。与线性内插相比，计算内插多项式的成本是昂贵的。此外，多项式插值可能会出现振荡伪像，特别是在端点。

6. 样条曲线插值

线性插值对每个区间$x_k,x_{k+1}$使用线性函数。 样条插值在每个间隔中使用低阶多项式，并选择多项式以使它们平滑地吻合在一起。 结果函数被称为样条曲线。例如，三次样条是分片段立方，两次连续可微。 此外，它的二阶导数在终点为零。 在上表中插入点的三次样条函数由下式给出
f ( x ) = { − 0.1522 x 3 + 0.9937 x , x ∈ [ 0 , 1 ] , − 0.01258 x 3 − 0.4189 x 2 + 1.4126 x − 0.1396 , x ∈ [ 1 , 2 ] , 0.1403 x 3 − 1.3359 x 2 + 3.2467 x − 1.3623 , x ∈ [ 2 , 3 ] , 0.1579 x 3 − 1.4945 x 2 + 3.7225 x − 1.8381 , x ∈ [ 3 , 4 ] , 0.05375 x 3 − 0.2450 x 2 − 1.2756 x + 4.8259 , x ∈ [ 4 , 5 ] , − 0.1871 x 3 + 3.3673 x 2 − 19.3370 x + 34.9282 , x ∈ [ 5 , 6 ] . f(x)={

$$\begin{cases}-0.1522x^{3}+0.9937x, \qquad x\in [0,1],\\-0.01258x^{3}-0.4189x^{2}+1.4126x-0.1396,\qquad x \in [1,2],\\0.1403x^{3}-1.3359x^{2}+3.2467x-1.3623,\qquad x\in [2,3],\\0.1579x^{3}-1.4945x^{2}+3.7225x-1.8381,\qquad x\in [3,4],\\0.05375x^{3}-0.2450x^{2}-1.2756x+4.8259,\qquad x\in [4,5],\\-0.1871x^{3}+3.3673x^{2}-19.3370x+34.9282,\qquad x\in [5,6].\end{cases}$$ } f(x)=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧​−0.1522x3+0.9937x,x∈[0,1],−0.01258x3−0.4189x2+1.4126x−0.1396,x∈[1,2],0.1403x3−1.3359x2+3.2467x−1.3623,x∈[2,3],0.1579x3−1.4945x2+3.7225x−1.8381,x∈[3,4],0.05375x3−0.2450x2−1.2756x+4.8259,x∈[4,5],−0.1871x3+3.3673x2−19.3370x+34.9282,x∈[5,6].​

在这种情况下，我们得到 f(2.5) = 0.5972。 与多项式插值的方法相比较，样条跟多项式一样，其插值误差会小于线性插值，而且插值更平滑；使用样条会比使用高阶多项式更容易评估。 它也不会受到龙格现象的影响。

7.牛顿插值

有关牛顿插值法的内容发表在大名鼎鼎的《自然哲学的数学原理》的第三卷的引理五中
牛顿多项式（英语：Newton Polynomial）是数值分析中一种用于插值的多项式。

因此，牛顿多项式可以写作：
$$N(x)=[y_0]+[y_0,y_1](x-x_0)+\cdots +[y_0,\dots ,y_k](x-x_0)(x-x_1)\cdots (x-x_{k-1})$$

总结上面的计算方法可以归纳出算法的大致思想：先计算差商表，类似于乘法口诀的思路，两个for循环就可以计算出，然后对于每一次内for循环以后，计算出了第一列，接着把相对应的f(x)计算出来，接着进入第二列的计算，接着计算相应的f(x)…一直到计算完毕最后一个f(x)，把所有的f(x)相加，便是最终的插值。

参考文献:
1.https://zh.wikipedia.org/wiki/%E6%8F%92%E5%80%BC
2.https://blog.csdn.net/zb1165048017/article/details/48343861
3.https://www.zhihu.com/question/22320408
4.https://zh.wikipedia.org/wiki/%E7%89%9B%E9%A1%BF%E5%A4%9A%E9%A1%B9%E5%BC%8F