- 12023年4月Web3行业月度发展报告区块链篇 | 陀螺科技会员专享
- 2ubuntu20.04安装完没有连接wifi的选项,ubuntu网卡驱动_ubuntu20.04没有连接wifi选项
- 3解决subprocess.CalledProcessError: Command ‘[‘dot‘, ‘-Tpdf‘, ‘-O‘, ‘Digraph.gv‘]‘ returned non-zero
- 4使用Golang创建windows GUI图形界面并添加图标_golang 图形界面
- 5Linux TCP/IP 网络工具对比:net-tools 和 iproute2_linux tcptool
- 6【就业必备知识】大学毕业如何处理档案和户口,小心变成死档和黑户_毕业户口没转出会变成黑户吗
- 7mqtt集群搭建并使用nginx做负载均衡_亲测得结论_mqtt负载均衡
- 8Unity 从0开始编写一个技能编辑器_01_分析需求_技能编辑器 unity
- 9【Python爬虫】基于selenium库爬取京东商品数据——以“七夕”为例_京东图书 selenium
- 10【C++基础入门】cLion的安装、搭建C++环境_clion创建c++项目
目标检测算法之AAAI2019 Oral论文GHM Loss
赞
踩
前言
这篇论文仍然是瞄准了One-Stage目标检测算法中的正负样本不均衡问题,上周我们介绍He Kaiming等人提出的Focal Loss,推文地址如下:https://mp.weixin.qq.com/s/2VZ_RC0iDvL-UcToEi93og 来解决样本不均衡的问题。但这篇论文提出,Focal Loss实际上是有问题的,论文论述了该问题并提出了GHM Loss更好的解决One-Stage目标检测算法中的正负样本不均衡问题。论文地址为:https://arxiv.org/pdf/1811.05181.pdf。github开源地址为:https://github.com/libuyu/GHM_Detection
梯度均衡机制(GHM)
首先论文引入了一个统计对象:梯度模长(gradient norm)。考虑一个简单的二元交叉熵函数(binar cross entropy loss):
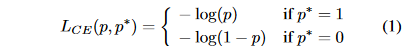
其中
p
=
s
i
g
m
o
i
d
(
x
)
p=sigmoid(x)
p=sigmoid(x)是模型预测的样本的类别概率,而
p
∗
p^{*}
p∗是标签信息,这样可以球处于其对
x
x
x的梯度:
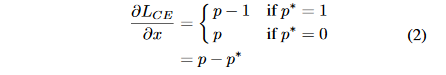 所以,论文定义了一个梯度模长为:
所以,论文定义了一个梯度模长为:
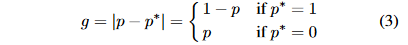 直观来看,
g
g
g表示了样本的真实值和预测值的距离。看下论文的Figure2,表示的是一个One-satge模型收敛后画出的梯度模长分布图。Figure2如下:
直观来看,
g
g
g表示了样本的真实值和预测值的距离。看下论文的Figure2,表示的是一个One-satge模型收敛后画出的梯度模长分布图。Figure2如下:
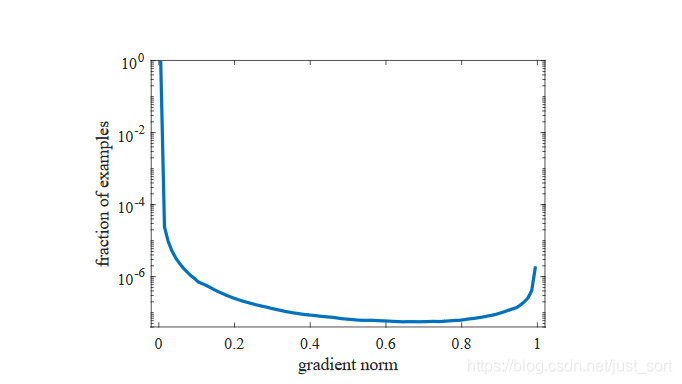
上图横坐标表示gradient norm,纵坐标表示数据分布的比例,做了对数尺度缩放,显然非常靠近y轴表示的是easy examples,非常靠近
x
=
1
x=1
x=1轴的表示very hard examples,中间部分的表示hard example。 重新标注下上图即:
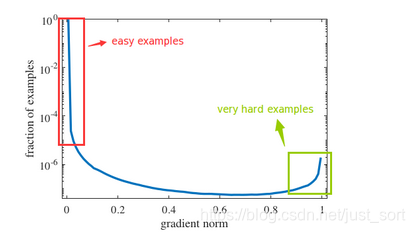 注意到途中绿框部分即为very hard example,论文认为这部分样本对模型的提升作用是没有帮助的,但这部分样本同样也有着较大的比例。根据Focal Loss的观点,我们班应该关注的是介于红框和绿框之间的样本,而Focal Loss缺不能解决这一点,而是把very hard examples也考虑在内了。这些very hard examples也被称为离群点,也就是说如果一个模型强行拟合了离群点,模型的泛化能力会变差,所以这篇论文提出了GHM Loss抑制离群点,取得了比Focal Loss更好的效果。
注意到途中绿框部分即为very hard example,论文认为这部分样本对模型的提升作用是没有帮助的,但这部分样本同样也有着较大的比例。根据Focal Loss的观点,我们班应该关注的是介于红框和绿框之间的样本,而Focal Loss缺不能解决这一点,而是把very hard examples也考虑在内了。这些very hard examples也被称为离群点,也就是说如果一个模型强行拟合了离群点,模型的泛化能力会变差,所以这篇论文提出了GHM Loss抑制离群点,取得了比Focal Loss更好的效果。
基于上面的分析,论文提出了梯度均衡机制(GHM),即根据样本梯度模长分布的比例,进行一个相应的标准化(normalization),使得各种类型的样本对模型参数的更新有更加均衡的贡献,进行让模型训练更高效可靠。由于梯度均衡本质上是对不同样本产生的梯度进行一个加权,进而改变它们的贡献量,而这个权重加在损失函数上也可以达到同样的效果,此研究中,梯度均衡机制便是通过重构损失函数来实现的。为了更加清楚的描述新的损失函数,论文定义了梯度密度(gradient density)这一概念。仿照物理上对于密度的定义(单位体积内的质量),论文把梯度密度定义为单位取值区域内分布的样本数量。
首先定义梯度密度函数(Gradient density function)
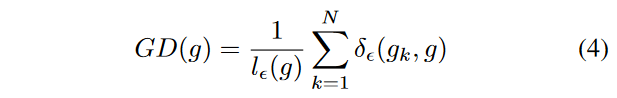 其中
g
k
g_k
gk表示第
k
k
k个样本的梯度,而且:
其中
g
k
g_k
gk表示第
k
k
k个样本的梯度,而且:
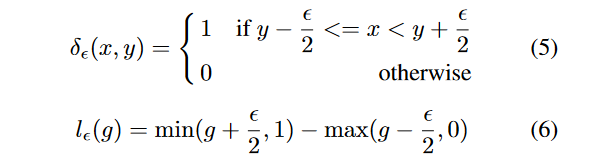 所以梯度密度函数
G
D
(
g
)
GD(g)
GD(g)就表示梯度落在区域
[
g
−
ϵ
2
,
g
+
ϵ
2
]
[g-\frac{\epsilon}{2},g+\frac{\epsilon}{2}]
[g−2ϵ,g+2ϵ]的样本数量。再定义度密度协调参数
β
\beta
β:
所以梯度密度函数
G
D
(
g
)
GD(g)
GD(g)就表示梯度落在区域
[
g
−
ϵ
2
,
g
+
ϵ
2
]
[g-\frac{\epsilon}{2},g+\frac{\epsilon}{2}]
[g−2ϵ,g+2ϵ]的样本数量。再定义度密度协调参数
β
\beta
β:
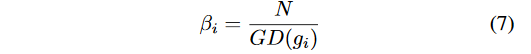 其中
N
N
N代表样本数量,是为了保证均匀分布或只划分一个单位区域时,该权值为 1,即 loss 不变。
其中
N
N
N代表样本数量,是为了保证均匀分布或只划分一个单位区域时,该权值为 1,即 loss 不变。
综上,我们可以看出梯度密度大的样本的权重会被降低,密度小的样本的权重会增加。于是把GHM的思想应用于分别应用于分类和回归上就形成了GHM-C和GHM-R。
用于分类的GHM Loss
把GHM应用于分类的loss上即为GHM-C,定义如下所示:
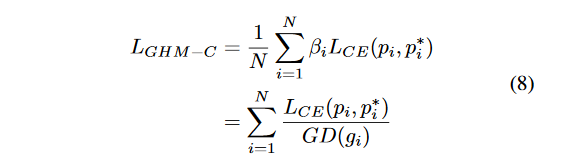 根据GHM-C的计算公式可以看出,候选样本的中的简单负样本和非常困难的异常样本(离群点)的权重都会被降低,即loss会被降低,对于模型训练的影响也会被大大减少,正常困难样本的权重得到提升,这样模型就会更加专注于那些更有效的正常困难样本,以提升模型的性能。GHM-C loss对模型梯度的修正效果如下图所示,横轴表示原始的梯度loss,纵轴表示修正后的。由于样本的极度不均衡,论文中所有的图纵坐标都是取对数画的图。注意这是Loss曲线,和上面的梯度模长曲线要加以区别。
根据GHM-C的计算公式可以看出,候选样本的中的简单负样本和非常困难的异常样本(离群点)的权重都会被降低,即loss会被降低,对于模型训练的影响也会被大大减少,正常困难样本的权重得到提升,这样模型就会更加专注于那些更有效的正常困难样本,以提升模型的性能。GHM-C loss对模型梯度的修正效果如下图所示,横轴表示原始的梯度loss,纵轴表示修正后的。由于样本的极度不均衡,论文中所有的图纵坐标都是取对数画的图。注意这是Loss曲线,和上面的梯度模长曲线要加以区别。
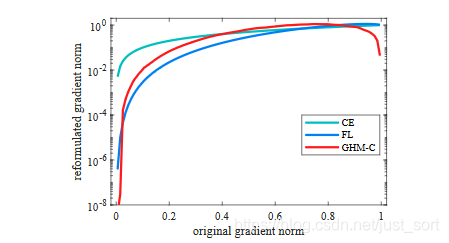 从上图可以看出,GHM-C和Focal Loss(FL)都对easy example做了很好的抑制,而GHM-C和Focal Loss在对very hard examples上有更好的抑制效果。同时因为原始定义的梯度密度函数计算计算太复杂,所以论文给出了一个梯度密度函数简化版本:
从上图可以看出,GHM-C和Focal Loss(FL)都对easy example做了很好的抑制,而GHM-C和Focal Loss在对very hard examples上有更好的抑制效果。同时因为原始定义的梯度密度函数计算计算太复杂,所以论文给出了一个梯度密度函数简化版本:
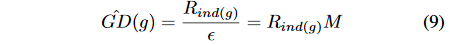
其中
i
n
d
(
g
)
=
t
,
(
t
−
1
)
ϵ
<
=
g
<
=
t
ϵ
ind(g)=t,(t-1)\epsilon<=g<=t\epsilon
ind(g)=t,(t−1)ϵ<=g<=tϵ。然后再结合密度协调函数
β
^
\hat{\beta}
β^:
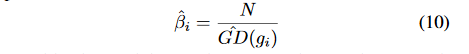 得到
L
G
H
M
−
C
^
\hat{L_{GHM-C}}
LGHM−C^为:
得到
L
G
H
M
−
C
^
\hat{L_{GHM-C}}
LGHM−C^为:
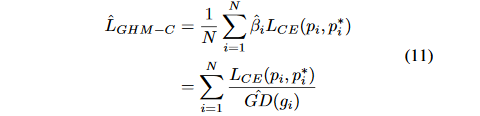
用于回归的GHM Loss
GHM的思想同样适用于Anchor的坐标回归。坐标回归的loss常用Smooth L1 Loss,如下图:
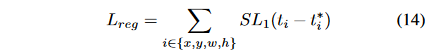
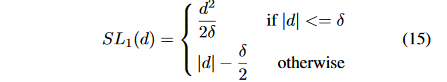 其中,
t
=
(
t
x
,
t
y
,
t
w
,
t
h
)
t=(t_x,t_y,t_w,t_h)
t=(tx,ty,tw,th)表示模型的预测坐标偏移值,
t
∗
=
(
t
x
∗
,
t
y
∗
,
t
w
∗
,
w
h
∗
)
t^*=(t_x^*,t_y^*,t_w^*,w_h^*)
t∗=(tx∗,ty∗,tw∗,wh∗)表示anchor相当于Ground Truth的实际坐标偏移量,
δ
\delta
δ表示
S
L
1
SL_1
SL1函数的分界点,常取
1
9
\frac{1}{9}
91。定义
d
=
t
i
−
t
i
∗
d=t_i-t_i^{*}
d=ti−ti∗,则
S
L
1
SL_1
SL1的梯度为:
其中,
t
=
(
t
x
,
t
y
,
t
w
,
t
h
)
t=(t_x,t_y,t_w,t_h)
t=(tx,ty,tw,th)表示模型的预测坐标偏移值,
t
∗
=
(
t
x
∗
,
t
y
∗
,
t
w
∗
,
w
h
∗
)
t^*=(t_x^*,t_y^*,t_w^*,w_h^*)
t∗=(tx∗,ty∗,tw∗,wh∗)表示anchor相当于Ground Truth的实际坐标偏移量,
δ
\delta
δ表示
S
L
1
SL_1
SL1函数的分界点,常取
1
9
\frac{1}{9}
91。定义
d
=
t
i
−
t
i
∗
d=t_i-t_i^{*}
d=ti−ti∗,则
S
L
1
SL_1
SL1的梯度为:
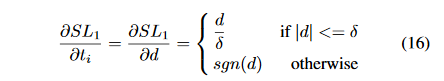 其中
s
g
n
sgn
sgn表示符号函数,当
∣
d
∣
>
=
δ
|d|>=\delta
∣d∣>=δ时,所有样本梯度绝对值都为1,这使我们无法通过梯度来区分样本,同时d理论上可以到无穷大,这也使我们无法根据梯度来估计一些example输出贡献度。基于此观察,论文对Smooth L1损失函数做了修正得到
A
S
L
1
ASL_1
ASL1:
其中
s
g
n
sgn
sgn表示符号函数,当
∣
d
∣
>
=
δ
|d|>=\delta
∣d∣>=δ时,所有样本梯度绝对值都为1,这使我们无法通过梯度来区分样本,同时d理论上可以到无穷大,这也使我们无法根据梯度来估计一些example输出贡献度。基于此观察,论文对Smooth L1损失函数做了修正得到
A
S
L
1
ASL_1
ASL1:
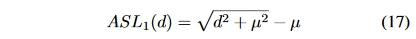 在论文中,
μ
=
0.02
\mu=0.02
μ=0.02。
在论文中,
μ
=
0.02
\mu=0.02
μ=0.02。
A
S
L
1
ASL_1
ASL1和Smooh L1损失有相似的性质,并且梯度为:
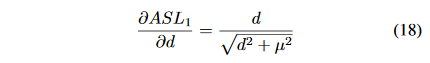 论文把
∣
d
d
2
+
μ
2
∣
|\frac{d}{\sqrt{d^2+\mu^2}}|
∣d2+μ2
d∣定义为梯度模长(gradient norm),则
A
S
L
1
ASL_1
ASL1的梯度模长和样本部分的关系如下图所示:
论文把
∣
d
d
2
+
μ
2
∣
|\frac{d}{\sqrt{d^2+\mu^2}}|
∣d2+μ2
d∣定义为梯度模长(gradient norm),则
A
S
L
1
ASL_1
ASL1的梯度模长和样本部分的关系如下图所示:
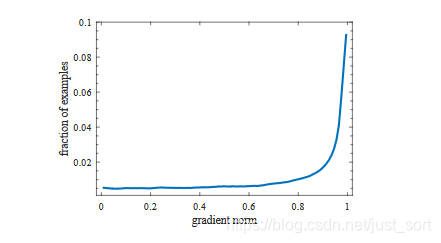
由于坐标回归都是正样本,所以简单样本的数量相对并不是很多。而且不同于简单负样本的分类对模型起反作用,简单正样本的回归梯度对模型十分重要。但是同样也可以看出来,存在相当数量的异常样本的回归梯度值很大。(图上最靠右的部分)。所以使用GHM的思想来修正loss函数,可以得到:
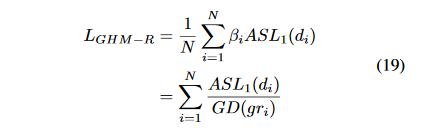 以达到对离群点的抑制作用。
以达到对离群点的抑制作用。
GHM-R Loss对于回归梯度的修正效果如下图所示:
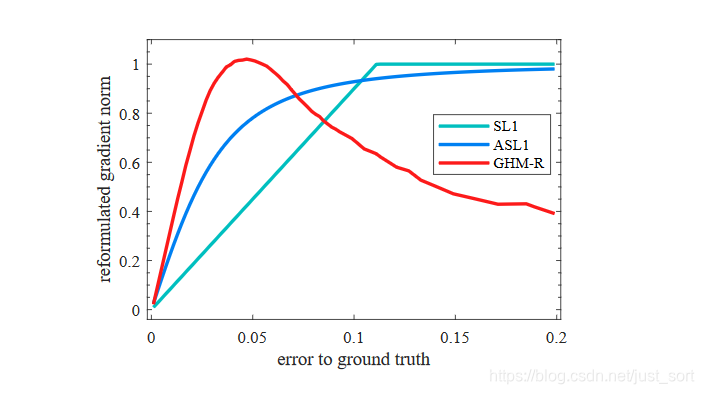 可以看到,GHM-R loss加大了简单样本和正常困难样本的权重,大大降低了异常样本的权重,使模型的训练更加合理。
可以看到,GHM-R loss加大了简单样本和正常困难样本的权重,大大降低了异常样本的权重,使模型的训练更加合理。
实验结论
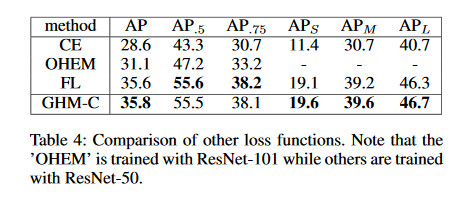
因为GHM-C和GHM-R是定义的损失函数,因此可以非常方便的嵌入到很多目标检测方法中,作者以focal loss(大概是以RetinaNet作为baseline),对交叉熵,focal loss和GHM-C做了对比,发现GHM-C在focal loss 的基础上在AP上提升了0.2个百分点。如表4所示。
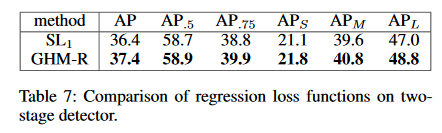
如果再用GHM-R代替双阶段检测器中的Smooth L1损失,那么AP值又会有提示。如表7所示。
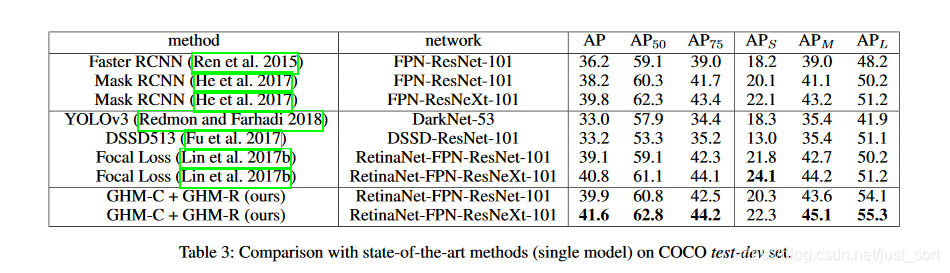
 如果同时把GHM-R Loss和GHM-C Loss用到目标检测器中,AP值有1-2个点提升。
如果同时把GHM-R Loss和GHM-C Loss用到目标检测器中,AP值有1-2个点提升。
后记
论文的大概思想就是这样,对于样本有不均衡的场景,我认为这个Loss是比较值得尝试的。
参考文章
https://blog.csdn.net/watermelon1123/article/details/89362220
https://zhuanlan.zhihu.com/p/80594704
欢迎关注我的微信公众号GiantPandaCV,期待和你一起交流机器学习,深度学习,图像算法,优化技术,比赛及日常生活等。


