因子分析模型R语言实现_r语言因子分析

前情回顾：因子分析模型Python版本

数据集展示

现有30个省份9项家庭支出指标，部分数据如下所示

现想通过因子分析法评价各省份家庭综合消费支出水平

一、KMO检验和Barlette检验

使用因子分析模型前，需保证各个变量存在相关性，检验的标准如下

library(psych) #KMO和Bartlette检验所需包
data<-read.csv('raw_data.csv')
data1=data[,-1] #去除地区列
KMO(data1)
bartlett.test(data1)
1
2
3
4
5

从检验结果来看，KMO值为0.88，Bartlette检验的P值远小于0.05，故该数据集十分适合作因子分析。

二、确定公因子个数

确定一般准则：特征值大于1或累计方差贡献率大于85%（这个值根据实际数据情况可以适当改变）

基本步骤：计算原始矩阵相关系数矩阵——计算相关系数矩阵的特征值——计算累计方差贡献率

这里使用累计方差贡献率确定公因子个数

corr=cor(data1) 
eig=eigen(corr)
(ccx=(eig$va)/sum(eig$va))  #贡献率
(cx=cumsum(eig$va)/sum(eig$va)) #累计方差贡献率
1
2
3
4

从结果可知，当公因子数为3个时，累计方差贡献率可达~90%，包含了原始数据的大部分信息。

三、正交旋转

正交旋转可使因子载荷矩阵中，各因子的值差别更大，有利于解释各因子含义

library(mvstats) #因子分析所需包
Fac0=factpc(scale(data1),3)
Fac1=factpc(scale(data1),3,rot="varimax")#运用旋转因子分析
data.frame(Fac0$loadings,row.names = colnames(data)[-1]) #旋转前的因子载荷矩阵
data.frame(Fac1$loadings,row.names = colnames(data)[-1]) #旋转后的因子载荷矩阵
1
2
3
4
5

旋转前的因子载荷矩阵特征：公共因子F1、F2、F3在原变量的载荷值差异不大，各个因子下的变量代表性并不突出

旋转后的因子载荷矩阵特征：公共因子F1在人均食品、教育、交通支出上载荷较大,可反映日常消费因子；F2在人均医疗支出上有很大的载荷,可视为医疗因子；F3在人均衣着支出上有很大的载荷,可视为衣着因子

四、因子得分

score=Fac1$scores  #各因子得分
rownames(score)=data$省份
plot.text(score[,1:2])  #因子1和因子2得分图
plot.text(score[,2:3])  #因子2和因子3得分图
1
2
3
4

从F1与F2的因子得分图来看：在F1因子上得分较高地区是上海、广东、北京、浙江、北京、福建,即这些地区的人均日常消费较高.而在F2因子上得分较高的地区是天津、北京、河北、吉林、辽宁,即这些地区的人均医疗支出较高.

从F2与F3的因子得分图来看：在F3因子上得分较高的地区是北京、上海、浙江、内蒙古、新疆,即这些地区的人均衣着支出较高.像新疆、内蒙古这些地区的人们,由于气候原因,人均衣着支出较多;而像北京、上海、浙江这些经济较发达地区的人们,为了追求更好的生活质量,人均衣着消费也位居前列.

综合F1、F2、F3因子得分情况来看，北京、上海、浙江这三个地区在三个因子上的得分都相对较高，可以知道这三个地区的综合消费水平位于我国消费水平前列.

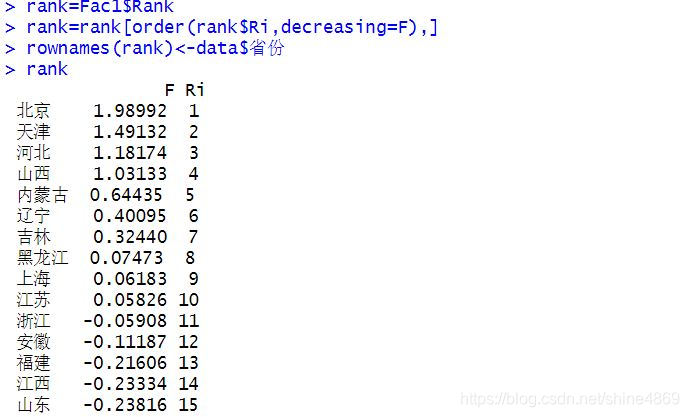
综合得分及排名

rank=Fac1$Rank #综合得分及排名
rownames(rank)<-data$省份
rank=rank[order(rank$Ri,decreasing=F),]
rank
1
2
3
4

全部代码

注意：mvstats包是王斌会教授自编的因子分析包，需要自行从网络上下载安装

library(mvstats)
library(psych) #KMO和Bartlette检验所需包
data<-read.csv('raw_data.csv')
data1=data[,-1] #去除地区列
KMO(data1)
bartlett.test(data1)

corr=cor(data1)
eig=eigen(corr)
(ccx=(eig$va)/sum(eig$va))  #贡献率
(cx=cumsum(eig$va)/sum(eig$va)) #累计方差贡献率

Fac0=factpc(scale(data1),3)
Fac1=factpc(scale(data1),3,rot="varimax")#运用旋转因子分析
data.frame(Fac0$loadings,row.names = colnames(data)[-1])
data.frame(Fac1$loadings,row.names = colnames(data)[-1])

score=Fac1$scores
rownames(score)=data$省份
plot.text(score[,1:2])
plot.text(score[,2:3])

rank=Fac1$Rank
rownames(rank)<-data$省份
rank=rank[order(rank$Ri,decreasing=F),]
rank
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

以上初步介绍了R语言版本因子分析的基本过程，后续会将多个年份的批量因子分析代码分享给大家~