- 1【硬石科技】电机系列教学(基于STM32)——舵机的控制_硬石stm
- 2电阻的知识大全_数字电路电阻名称
- 3config设置源 使用pip_最全的 pip 使用指南,50 % 你可能都没用过~
- 4ffmpeg视频处理常用命令
- 5分布式事务选型及对比_保证分布式事务一致性 方案 seata rocketmq
- 6Error inflating class com.google.android.material.bottomnavigation.BottomNavigationView
- 7【华为HCIP | 华为数通工程师】刷题日记1116(一个字惨)_用户可以通过更改优先级手动指定ip地址拥有者
- 8节省时间的分层测试,到底怎么做?_分层测试思路怎么写
- 9环境变量详解_bash: export: `path/opt/jdk-11.0.15.1/bin:/usr/loc
- 10鸿蒙App开发(1)---初识鸿蒙开发
浅易理解:卷积神经网络(CNN)
赞
踩
浅易理解卷积神经网络流程
本文的目录:
1 什么卷积神经网络
2 输入层
3 卷积层
4 池化层
5 全连接层
传统的多层神经网络只有 输入层、隐藏层、输出层
卷积神经网络(CNN):
在多层神经网络的基础上,加入了更加有效的特征学习部分,具体就是在全连接层前加入了卷积层与池化层,卷积神经网络出现,使得神经网络层数得以加深,“深度学习”由此而来。
还可以用卷积层、激活层、池化层(又叫下采样层)、全连接层表示。
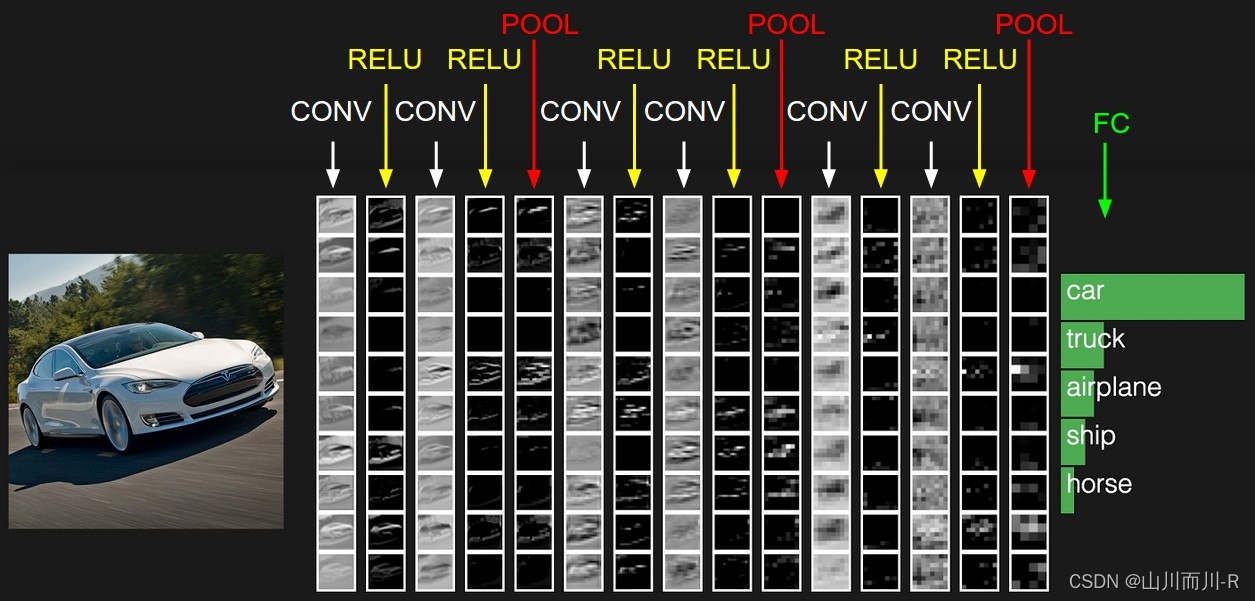
1 什么是卷积神经网络
1.1卷积神经网络(Convolutional Neural Networks, CNN)
是一种前馈神经网络,它的人工神经元可以响应一部分覆盖范围内的周围单元,对于大型图像处理有出色表现。 它包括卷积层(convolutional layer)和池化层(pooling layer)。
1.2卷积神经网络整个运算过程:
- 输入层:输入图像等信息
- 卷积层:用来提取图像的底层特征
- 池化层:防止过拟合,将数据维度减小
- 全连接层:汇总卷积层和池化层得到的图像的底层特征和信息
- 输出层:根据全连接层的信息得到概率最大的结果
其中最重要的一层就是卷积层,这也是卷积神经网络名称的由来
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
1.3什么是卷积
对图像(不同的数据窗口数据)和滤波矩阵(一组固定的权重:因为每个神经元的多个权重固定,所以又可以看做一个恒定的滤波器filter)做内积(逐个元素相乘再求和)的操作就是所谓的『卷积』操作,也是卷积神经网络的名字来源。
非严格意义上来讲,下图中红框框起来的部分便可以理解为一个滤波器,即带着一组固定权重的神经元。多个滤波器叠加便成了卷积层。
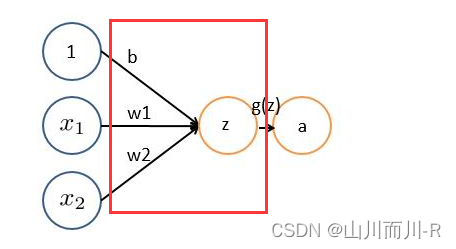
基本wx + b的形式,其中
、
表示输入向量
、
为权重,几个输入则意味着有几个权重,即每个输入都被赋予一个权重
- b为偏置bias
- g(z) 为激活函数
- a 为输出
如果只是上面这样一说,估计以前没接触过的十有八九又必定迷糊了。事实上,上述简单模型可以追溯到20世纪50/60年代的感知器,可以把感知器理解为一个根据不同因素、以及各个因素的重要性程度而做决策的模型。
举个例子,这周末北京有一草莓音乐节,那去不去呢?决定你是否去有二个因素,这二个因素可以对应二个输入,分别用x1、x2表示。此外,这二个因素对做决策的影响程度不一样,各自的影响程度用权重w1、w2表示。一般来说,音乐节的演唱嘉宾会非常影响你去不去,唱得好的前提下 即便没人陪同都可忍受,但如果唱得不好还不如你上台唱呢。所以,我们可以如下表示:
:是否有喜欢的演唱嘉宾。 = 1 你喜欢这些嘉宾, = 0 你不喜欢这些嘉宾。嘉宾因素的权重 = 7
:是否有人陪你同去。 = 1 有人陪你同去, = 0 没人陪你同去。是否有人陪同的权重 = 3。
这样,咱们的决策模型便建立起来了:g(z) = g( * + * + b ),g表示激活函数,这里的b可以理解成 为更好达到目标而做调整的偏置项。
一开始为了简单,人们把激活函数定义成一个线性函数,即对于结果做一个线性变化,比如一个简单的线性激活函数是g(z) = z,输出都是输入的线性变换。后来实际应用中发现,线性激活函数太过局限,于是人们引入了非线性激活函数。
+++++++++++++++++++++++++++++++++++++++++++++++++++++
具体的例子。比如下图中,图中左边部分是原始输入数据,图中中间部分是滤波器filter,图中右边是输出的新的二维数据。
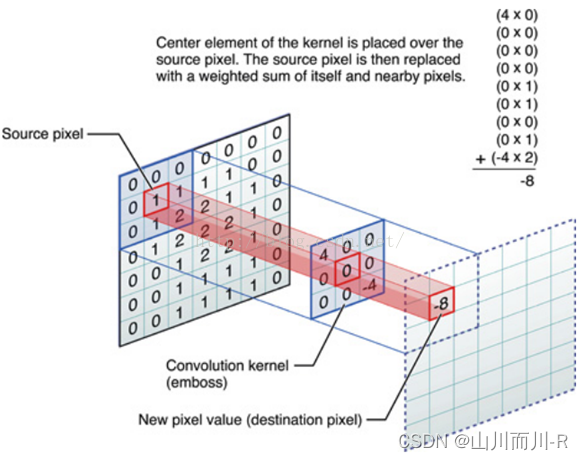
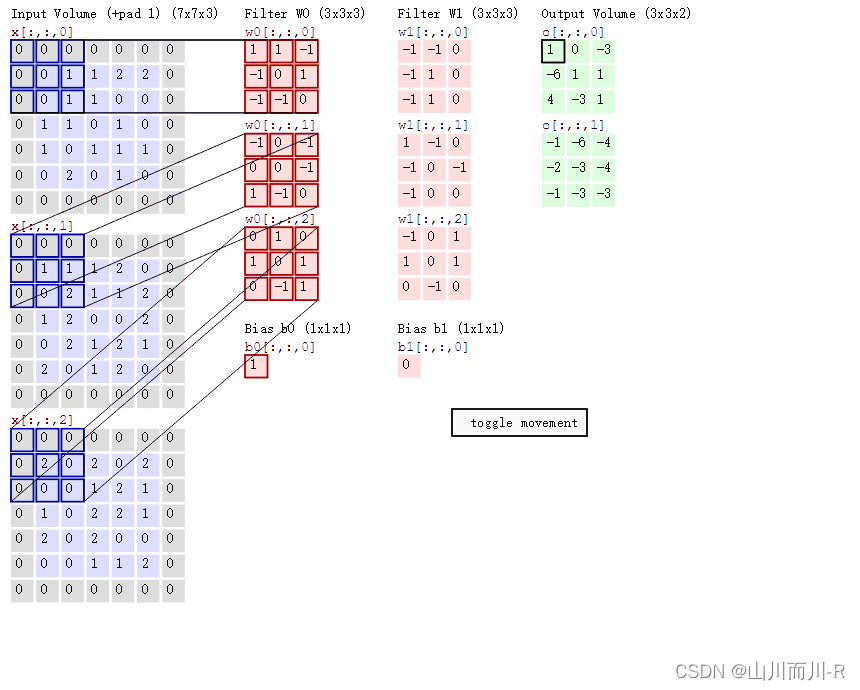
即上图中的输出结果1具体是怎么计算得到的呢?其实,类似wx + b,w对应滤波器Filter w0,x对应不同的数据窗口,b对应Bias b0,相当于滤波器Filter w0与一个个数据窗口相乘再求和后,最后加上Bias b0得到输出结果1:
可以看到:
两个神经元,即depth=2,意味着有两个滤波器。
数据窗口每次移动两个步长取3*3的局部数据,即stride=2。
zero-padding=1。
然后分别以两个滤波器filter为轴滑动数组进行卷积计算,得到两组不同的结果。
如果初看上图,可能不一定能立马理解啥意思,但结合上文的内容后,理解这个动图已经不是很困难的事情:
左边是输入(7*7*3中,7*7代表图像的像素/长宽,3代表R、G、B 三个颜色通道)
中间部分是两个不同的滤波器Filter w0、Filter w1
最右边则是两个不同的输出
随着左边数据窗口的平移滑动,滤波器Filter w0 / Filter w1对不同的局部数据进行卷积计算。
值得一提的是:左边数据在变化,每次滤波器都是针对某一局部的数据窗口进行卷积,这就是所谓的CNN中的局部感知机制。
打个比方,滤波器就像一双眼睛,人类视角有限,一眼望去,只能看到这世界的局部。如果一眼就看到全世界,你会累死,而且一下子接受全世界所有信息,你大脑接收不过来。当然,即便是看局部,针对局部里的信息人类双眼也是有偏重、偏好的。比如看美女,对脸、胸、腿是重点关注,所以这3个输入的权重相对较大。
与此同时,数据窗口滑动,导致输入在变化,但中间滤波器Filter w0的权重(即每个神经元连接数据窗口的权重)是固定不变的,这个权重不变即所谓的CNN中的参数(权重)共享机制。
再打个比方,某人环游全世界,所看到的信息在变,但采集信息的双眼不变。btw,不同人的双眼 看同一个局部信息 所感受到的不同,即一千个读者有一千个哈姆雷特,所以不同的滤波器 就像不同的双眼,不同的人有着不同的反馈结果。
看到上面这个动态图的时候,计算过程是“相乘后相加”,但到底具体是个怎么相乘后相加的计算过程 则无法一眼看出,网上也没有一目了然的计算过程。本文来细究下。
计算过程是“相乘后相加”
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
1.4 人工神经网络
1.4.1 神经元
在人工智能领域中,人工神经元是对生物神经元进行模拟的概念模型,它是构建人工神经网络的基本单元。人工神经元的设计意图是模仿生物大脑中神经元处理信息的方式,即接收输入信号、对信号进行加权处理并产生输出响应的能力。
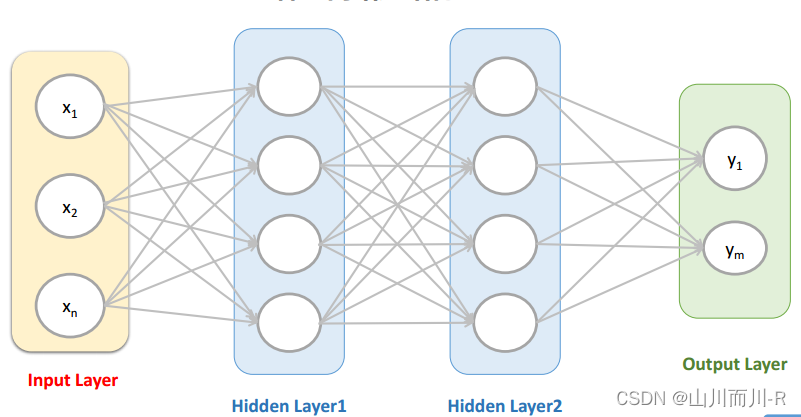
将下图的这种单个神经元:
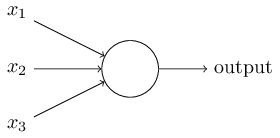
组织在一起,便形成了神经网络。下图便是一个三层神经网络结构

上图中最左边的原始输入信息称之为输入层,最右边的神经元称之为输出层(上图中输出层只有一个神经元),中间的叫隐藏层。
什么叫输入层、输出层、隐藏层?
输入层(Input layer),众多神经元(Neuron)接受大量非线形输入讯息。输入的讯息称为输入向量。
输出层(Output layer),讯息在神经元链接中传输、分析、权衡,形成输出结果。输出的讯息称为输出向量。
隐藏层(Hidden layer),简称“隐层”,是输入层和输出层之间众多神经元和链接组成的各个层面。如果有多个隐藏层,则意味着多个激活函数。
同时,每一层都可能由单个或多个神经元组成,每一层的输出将会作为下一层的输入数据。如中间隐藏层来说,隐藏层的3个神经元a1、a2、a3皆各自接受来自多个不同权重的输入(因为有x1、x2、x3这三个输入,所以a1 a2 a3都会接受x1 x2 x3各自分别赋予的权重,即几个输入则几个权重),接着,a1、a2、a3又在自身各自不同权重的影响下 成为的输出层的输入,最终由输出层输出最终结果。
此外,上文中讲的都是一层隐藏层,但实际中也有多层隐藏层的,即输入层和输出层中间夹着数层隐藏层,层和层之间是全连接的结构,同一层的神经元之间没有连接。
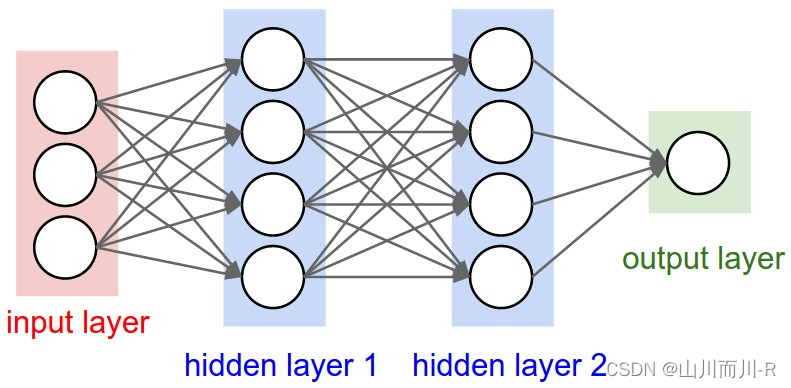
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
1.5 激活函数
常用的非线性激活函数有sigmoid、tanh、relu等等,前两者sigmoid/tanh比较常见于全连接层,后者relu常见于卷积层。这里先简要介绍下最基础的sigmoid函数(btw,在本博客中SVM那篇文章开头有提过)
sigmoid的函数表达式如下:
sigmoid函数的数学表达式如下:
![]()
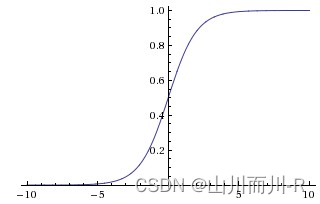
其中 x 是该函数的输入变量。sigmoid函数将输入 x 映射到 (0, 1) 区间内,呈现出S形曲线的特点,常用于神经网络作为激活函数,尤其是在二分类问题中,输出可以解释为属于某一类的概率。随着 x 值增加,sigmoid函数的输出值逐渐逼近1;随着 x值减少,输出值逐渐逼近0。
其中z是一个线性组合,比如z可以等于:b + 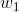
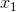
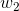
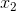
因此,sigmoid函数g(z)的图形表示如下( 横轴表示定义域z,纵轴表示值域g(z) ):
也就是说,sigmoid函数的功能是相当于把一个实数压缩至0到1之间。当z是非常大的正数时,g(z)会趋近于1,而z是非常小的负数时,则g(z)会趋近于0。
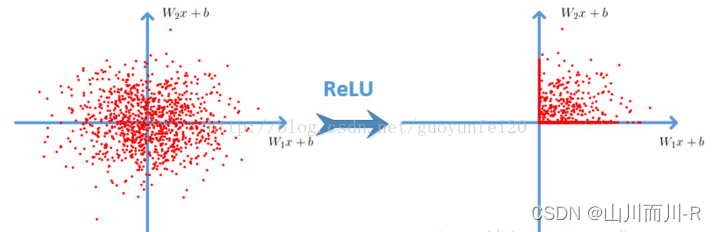
激活函数:ReLU
Relu函数:f(x)=max(0,x)
采用非饱和线性单元——ReLU代替传统的经常使用的tanh和sigmoid函数,加速了网络训练的速度,降低了计算的复杂度,对各种干扰更加具有鲁棒性,并且在一定程度上避免了梯度消失问题。
优势:
- ReLU本质上是分段线性模型,前向计算非常简单,无需指数之类操作;
- ReLU的偏导也很简单,反向传播梯度,无需指数或者除法之类操作;
- ReLU不容易发生梯度发散问题,Tanh和Logistic激活函数在两端的时候导数容易趋近于零,多级连乘后梯度更加约等于0;
- ReLU关闭了右边,从而会使得很多的隐层输出为0,即网络变得稀疏,起到了类似L1的正则化作用,可以在一定程度上缓解过拟合。
缺点:
当然,ReLU也是有缺点的,比如左边全部关了很容易导致某些隐藏节点永无翻身之日,所以后来又出现pReLU、random ReLU等改进,而且ReLU会很容易改变数据的分布,因此ReLU后加Batch Normalization也是常用的改进的方法。
在PyTorch中使用ReLU激活函数的API调用示例:
- import torch.nn as nn
-
- # 定义一个模块,包含ReLU激活函数
- class MyModel(nn.Module):
- def __init__(self):
- super(MyModel, self).__init__()
- self.linear = nn.Linear(in_features=100, out_features=64)
- self.relu = nn.ReLU()
-
- def forward(self, x):
- x = self.linear(x)
- x = self.relu(x) # 应用ReLU激活函数
- return x
在Keras中使用ReLU激活函数的API调用示例:
- from tensorflow.keras.layers import Activation
-
- # 创建一个ReLU激活层
- relu_activation = Activation('relu')
-
- # 或者在构造卷积层或全连接层时直接指定激活函数
- from tensorflow.keras.layers import Dense
-
- dense_layer = Dense(units=64, activation='relu') # 使用ReLU作为激活函数
在PaddlePaddle中使用ReLU激活函数的API调用示例:
- import paddle.nn as nn
- 2
- 3# 创建一个ReLU激活层
- 4relu = nn.ReLU()
- 5
- 6# 或者在构造卷积层时直接指定ReLU作为激活函数
- 7conv2d_layer = nn.Conv2D(in_channels=3, out_channels=64, kernel_size=3, stride=1, padding=1, activation='relu')
为什么输入数据需要归一化(Normalized Data)
归一化后有什么好处呢?原因在于神经网络学习过程本质就是为了学习数据分布,一旦训练数据与测试数据的分布不同,那么网络的泛化能力也大大降低;另外一方面,一旦每批训练数据的分布各不相同(batch 梯度下降),那么网络就要在每次迭代都去学习适应不同的分布,这样将会大大降低网络的训练速度,这也正是为什么我们需要对数据都要做一个归一化预处理的原因。
对于深度网络的训练是一个复杂的过程,只要网络的前面几层发生微小的改变,那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变,那么这一层网络就需要去适应学习这个新的数据分布,所以如果训练过程中,训练数据的分布一直在发生变化,那么将会影响网络的训练速度。
组成图片的最基本单位是像素
分布式计算:
AlexNet使用CUDA加速深度卷积网络的训练,利用GPU强大的并行计算能力,处理神经网络训练时大量的矩阵运算,AlexNet使用两个GTX580的GPU进行训练,单个GTX580只有3GB的显存,限制了可训练网络的最大规模,因此将其分布在两个GPU上,在每个GPU的显存中储存一般的神经元参数。
区域 CNN:R-CNN(2013年)、Fast R-CNN(2015年)、Faster R-CNN(2015年)
生成式对抗网络
生成对抗网络,假设有两个模型,一个生成模型,一个判别模型。判别模型的任务是决定某幅图像是真实的(来自数据库),还是机器生成的,而生成模型的任务则是生成能够骗过判别模型的图像。这两个模型彼此就形成了“对抗”,发展下去最终会达到一个平衡,生成器生成的图像与真实的图像没有区别,判别器无法区分两者。
//+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++//
2 输入层
输入图像,将其转换为对应的二维矩阵,这个二位矩阵就是由图像每一个像素的像素值大小组成的,一个例子,如下图所示的手写数字“8”的图像,计算机读取以像素值大小组成的二维矩阵存储的图像。

上图又称为灰度图像,因为其每一个像素值的范围是0~255(由纯黑色到纯白色),表示其颜色强弱程度。另外还有黑白图像,每个像素值要么是0(表示纯黑色),要么是255(表示纯白色)。我们日常生活中最常见的就是RGB图像,有三个通道,分别是红色、绿色、蓝色。每个通道的每个像素值的范围也是0~255,表示其每个像素的颜色强弱。但是我们日常处理的基本都是灰度图像,因为比较好操作(值范围较小,颜色较单一),有些RGB图像在输入给神经网络之前也被转化为灰度图像,也是为了方便计算,否则三个通道的像素一起处理计算量非常大。随着计算机性能的高速发展,现在有些神经网络也可以处理三通道的RGB图像。
输入层的作用就是将图像转换为其对应的由像素值构成的二维矩阵,并将此二维矩阵存储。
//+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++//
3 卷积层
3.1 CNN怎么进行识别
通过卷积运算我们可以提取出图像的特征,通过卷积运算可以使得原始信号的某些特征增强,并且降低噪声。
用一个滤波器fx去卷积一个输入的图像(第一阶段是输入的图像,后面的阶段就是卷积特征map了),然后加一个偏置bx,得到卷积层Cx。
下采样层:因为对图像进行下采样,可以减少数据处理量同时保留有用信息,采样可以混淆特征的具体位置,因为某个特征找出来之后,它的位置已经不重要了,我们只需要这个特征和其他特征的相对位置,可以应对形变和扭曲带来的同类物体的变化。
每邻域四个像素求和变为一个像素,然后通过标量Wx+1加权,再增加偏置bx+1,然后通过一个sigmoid激活函数,产生一个大概缩小四倍的特征映射图Sx+1。
3.2过滤器(卷积核)
在卷积运算时,会给定一个大小为F*F的方阵,称为过滤器,又叫做卷积核,该矩阵的大小又称为感受野。过滤器的深度d和输入层的深度d维持一致,因此可以得到大小为F*F*d的过滤器,从数学的角度出发,其为d个F*F的矩阵。在实际的操作中,不同的模型会确定不同数量的过滤器,其个数记为K,每一个K包含d个F*F的矩阵,并且计算生成一个输出矩阵。
一定大小的输入和一定大小的过滤器,再加上一些额外参数,会生成确定大小的输出矩阵。以下先介绍这些参数。
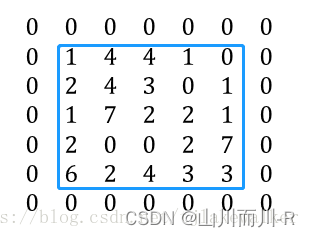
3.3 Padding
在进行卷积运算时,输入矩阵的边缘会比矩阵内部的元素计算次数少,且输出矩阵的大小会在卷积运算中相比较于输入变小。因此,可在输入矩阵的四周补零,称为padding,其大小为P。比如当P=1时,原5*5的矩阵如下,蓝色框中为原矩阵,周围使用0作为padding。
- from tensorflow.keras.layers import Conv2D
-
- # 在Keras中创建一个卷积层并指定'padding'参数
- conv_layer = Conv2D(filters=32, kernel_size=(3, 3), strides=1, padding='same')
在这个例子中,kernel_size=(3, 3)意味着使用的是3x3大小的卷积核,而padding='same'表示我们想要保持输入和输出在空间维度上的尺寸相同。如果改为padding='valid',则不会有额外的填充,输出尺寸将会减小。
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
3.4 卷积的感受野
3.4.1感受野的概念
在卷积神经网络中,感受野(Receptive Field)的定义是卷积神经网络每一层输出的特征图(feature map)上的像素点在输入图片上映射的区域大小。再通俗点的解释是,特征图上的一个点对应输入图上的区域,如图1所示。
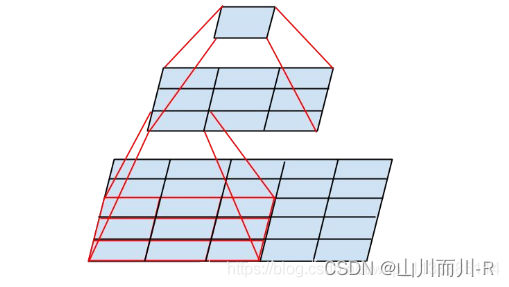
//+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++//
4 池化层
4.1 池化层的作用
池化层的作用:是对卷积层中提取的特征进行挑选。
常见的池化操作有最大池化和平均池化,池化层是由n×n大小的矩阵窗口滑动来进行计算的,类似于卷积层,只不过不是做互相关运算,而是求n×n大小的矩阵中的最大值、平均值等。
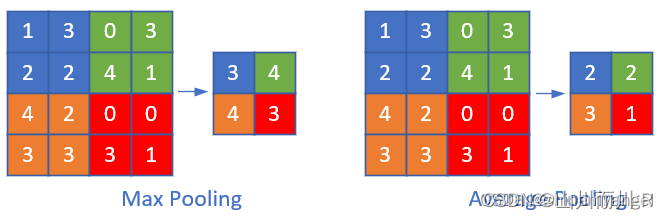
池化层主要有以下几个作用:
1. 挑选不受位置干扰的图像信息。
2. 对特征进行降维,提高后续特征的感受野,也就是让池化后的一个像素对应前面图片中的一个区域。
3. 因为池化层是不进行反向传播的,而且池化层减少了特征图的变量个数,所以池化层可以减少计算量。
//++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++//
5 全连接层
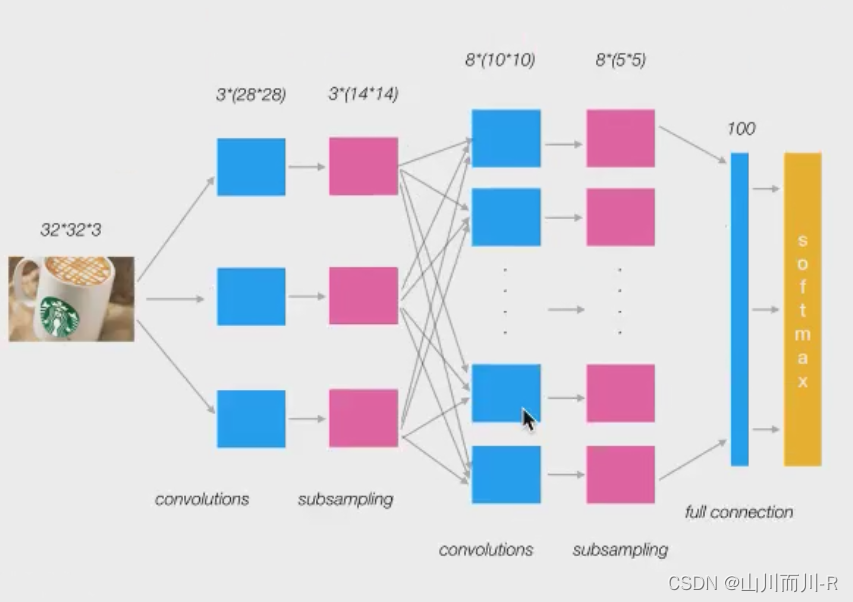
池化层的后面一般接着全连接层,全连接层将池化层的所有特征矩阵转化成一维的特征大向量,全连接层一般放在卷积神经网络结构中的最后,用于对图片进行分类,到了全连接层,我们的神经网络就要准备输出结果了
如下图所示,倒数第二列的向量就是全连接层的数据
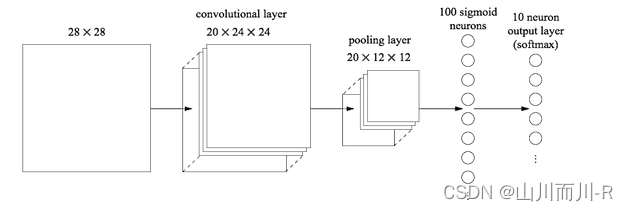
从池化层到全连接层会进行池化操作,数据会进行多到少的映射,进行降维,也就是为什么上图从20×12×12变成100个神经元了,数据在慢慢减少,说明离输出结果越来越近,从全连接层到输出层会再一次减少数据,变成更加低维的向量,这个向量的维度就是需要输出的类别数。然后将这个向量的每个值转换成概率的表示,这个操作一般叫做softmax,softmax使得向量中每个值范围在(0,1)之间,它是二分类函数sigmoid在多分类上的推广,目的是将多分类的结果以概率的形式展现出来。
5.1 全连接层的作用
因为从卷积层过来的数据太多了,全连接层的作用主要是对数据进行降维操作,不然数据骤降到输出层,可能会丢失一些图像特征的重要信息。
6 案例
下面是一个使用Keras库构建的简单卷积神经网络(CNN)案例,该网络用于解决MNIST手写数字识别问题:
- # 导入所需库
- from tensorflow.keras.datasets import mnist
- from tensorflow.keras.models import Sequential
- from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense
-
- # 加载MNIST数据集
- (x_train, y_train), (x_test, y_test) = mnist.load_data()
-
- # 数据预处理
- x_train = x_train.reshape(-1, 28, 28, 1).astype('float32') / 255.0
- x_test = x_test.reshape(-1, 28, 28, 1).astype('float32') / 255.0
- y_train = tf.keras.utils.to_categorical(y_train, 10)
- y_test = tf.keras.utils.to_categorical(y_test, 10)
-
- # 构建卷积神经网络模型
- model = Sequential([
- Conv2D(32, kernel_size=(3, 3), activation='relu', input_shape=(28, 28, 1)),
- MaxPooling2D(pool_size=(2, 2)),
- Conv2D(64, kernel_size=(3, 3), activation='relu'),
- MaxPooling2D(pool_size=(2, 2)),
- Flatten(),
- Dense(128, activation='relu'),
- Dense(10, activation='softmax') # 输出层,对应10个数字类别
- ])
-
- # 编译模型
- model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
-
- # 训练模型
- model.fit(x_train, y_train, batch_size=128, epochs=10, validation_data=(x_test, y_test))
-
- # 评估模型
- test_loss, test_acc = model.evaluate(x_test, y_test)
- print(f'Test accuracy: {test_acc}')

这个简单的卷积神经网络包含两个卷积层(Conv2D)和两个最大池化层(MaxPooling2D),然后通过Flatten层展平数据,接着连接两个全连接层(Dense),最后是10个节点的输出层,采用softmax激活函数用于多分类任务。整个模型使用Adam优化器进行编译,并以交叉熵损失函数为目标进行训练。
7 常用框架
Caffe
•源于Berkeley的主流CV工具包,支持C++,python,matlab
•Model Zoo中有大量预训练好的模型供使用
PyTorch
•Facebook用的卷积神经网络工具包
•通过时域卷积的本地接口,使用非常直观
•定义新网络层简单
TensorFlow
•Google的深度学习框架
•TensorBoard可视化很方便
•数据和模型并行化好,速度快
感知机:
PlayGround
http://playground.tensorflow.org
PlayGround是一个在线演示、实验的神经网络平台,是一个入门神经网络非常直观的网站。这个图形化平台非常强大,将神经网络的训练过程直接可视化。同时也能让我们对Tensorflow有一个感性的认识。
PlayGround页面如图所示,主要分为DATA(数据),FEATURES(特征),HIDDEN LAYERS(隐含层),OUTPUT(输出层)。
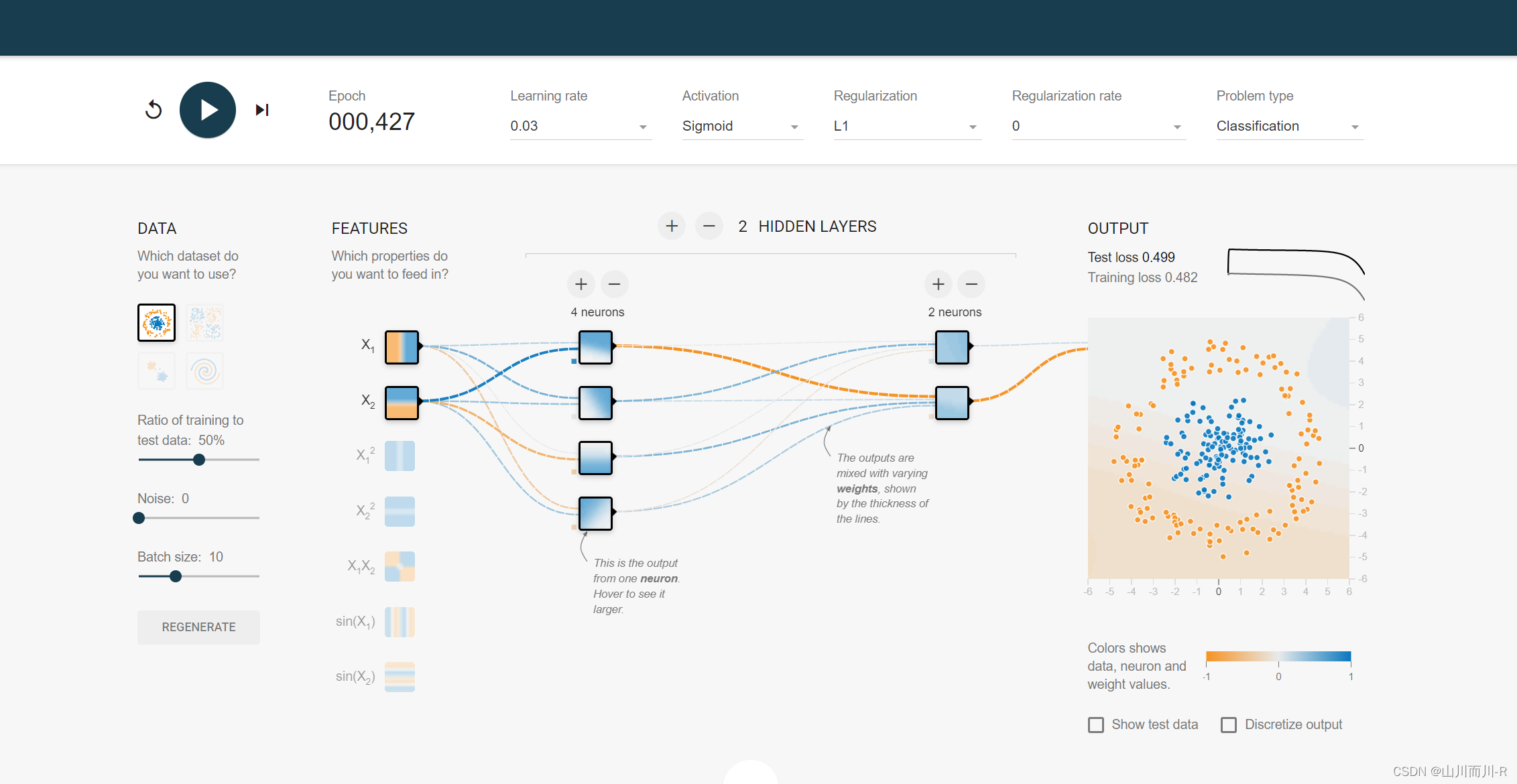
最后代码实现手写字体识别
- import tensorflow as tf
- import os
- from tensorflow.examples.tutorials.mnist import input_data
- from tensorflow.contrib.slim.python.slim.nets.inception_v3 import inception_v3_base
-
-
- # 1、利用数据,在训练的时候实时提供数据
- # mnist手写数字数据在运行时候实时提供给给占位符
-
- tf.app.flags.DEFINE_integer("is_train", 1, "指定是否是训练模型,还是拿数据去预测")
- FLAGS = tf.app.flags.FLAGS
-
-
- def create_weights(shape):
- return tf.Variable(initial_value=tf.random_normal(shape=shape, stddev=0.01))
-
-
- def create_model(x):
- """
- 构建卷积神经网络
- :param x:
- :return:
- """
- # 1)第一个卷积大层
- with tf.variable_scope("conv1"):
-
- # 卷积层
- # 将x[None, 784]形状进行修改
- input_x = tf.reshape(x, shape=[-1, 28, 28, 1])
- # 定义filter和偏置
- conv1_weights = create_weights(shape=[5, 5, 1, 32])
- conv1_bias = create_weights(shape=[32])
- conv1_x = tf.nn.conv2d(input=input_x, filter=conv1_weights, strides=[1, 1, 1, 1], padding="SAME") + conv1_bias
-
- # 激活层
- relu1_x = tf.nn.relu(conv1_x)
-
- # 池化层
- pool1_x = tf.nn.max_pool(value=relu1_x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="SAME")
-
- # 2)第二个卷积大层
- with tf.variable_scope("conv2"):
-
- # 卷积层
- # 定义filter和偏置
- conv2_weights = create_weights(shape=[5, 5, 32, 64])
- conv2_bias = create_weights(shape=[64])
- conv2_x = tf.nn.conv2d(input=pool1_x, filter=conv2_weights, strides=[1, 1, 1, 1], padding="SAME") + conv2_bias
-
- # 激活层
- relu2_x = tf.nn.relu(conv2_x)
-
- # 池化层
- pool2_x = tf.nn.max_pool(value=relu2_x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="SAME")
-
- # 3)全连接层
- with tf.variable_scope("full_connection"):
- # [None, 7, 7, 64]->[None, 7 * 7 * 64]
- # [None, 7 * 7 * 64] * [7 * 7 * 64, 10] = [None, 10]
- x_fc = tf.reshape(pool2_x, shape=[-1, 7 * 7 * 64])
- weights_fc = create_weights(shape=[7 * 7 * 64, 10])
- bias_fc = create_weights(shape=[10])
- y_predict = tf.matmul(x_fc, weights_fc) + bias_fc
-
- return y_predict
-
-
- def full_connected_mnist():
- """
- 单层全连接神经网络识别手写数字图片
- 特征值:[None, 784]
- 目标值:one_hot编码 [None, 10]
- :return:
- """
- mnist = input_data.read_data_sets("./mnist_data/", one_hot=True)
- # 1、准备数据
- # x [None, 784] y_true [None. 10]
- with tf.variable_scope("mnist_data"):
- x = tf.placeholder(tf.float32, [None, 784])
- y_true = tf.placeholder(tf.int32, [None, 10])
-
- y_predict = create_model(x)
-
- # 3、softmax回归以及交叉熵损失计算
- with tf.variable_scope("softmax_crossentropy"):
- # labels:真实值 [None, 10] one_hot
- # logits:全脸层的输出[None,10]
- # 返回每个样本的损失组成的列表
- loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_true, logits=y_predict))
-
- # 4、梯度下降损失优化
- with tf.variable_scope("optimizer"):
- # 学习率
- train_op = tf.train.AdamOptimizer(0.001).minimize(loss)
-
- # 5、得出每次训练的准确率(通过真实值和预测值进行位置比较,每个样本都比较)
- with tf.variable_scope("accuracy"):
- equal_list = tf.equal(tf.argmax(y_true, 1), tf.argmax(y_predict, 1))
- accuracy = tf.reduce_mean(tf.cast(equal_list, tf.float32))
-
- # (2)收集要显示的变量
- # 先收集损失和准确率
- tf.summary.scalar("losses", loss)
- tf.summary.scalar("acc", accuracy)
-
- # 初始化变量op
- init_op = tf.global_variables_initializer()
-
- # (3)合并所有变量op
- merged = tf.summary.merge_all()
-
- # 创建模型保存和加载
- saver = tf.train.Saver()
-
- # 开启会话去训练
- with tf.Session() as sess:
- # 初始化变量
- sess.run(init_op)
-
- # (1)创建一个events文件实例
- file_writer = tf.summary.FileWriter("./tmp/summary/", graph=sess.graph)
-
- # 加载模型
- # if os.path.exists("./tmp/modelckpt/checkpoint"):
- # saver.restore(sess, "./tmp/modelckpt/fc_nn_model")
-
- if FLAGS.is_train == 1:
- # 循环步数去训练
- for i in range(3000):
- # 获取数据,实时提供
- # 每步提供50个样本训练
- mnist_x, mnist_y = mnist.train.next_batch(50)
- # 运行训练op
- sess.run(train_op, feed_dict={x: mnist_x, y_true: mnist_y})
- print("训练第%d步的准确率为:%f, 损失为:%f " % (i+1,
- sess.run(accuracy, feed_dict={x: mnist_x, y_true: mnist_y}),
- sess.run(loss, feed_dict={x: mnist_x, y_true: mnist_y})
- )
- )
-
- # 运行合变量op,写入事件文件当中
- summary = sess.run(merged, feed_dict={x: mnist_x, y_true: mnist_y})
- file_writer.add_summary(summary, i)
- # if i % 100 == 0:
- # saver.save(sess, "./tmp/modelckpt/fc_nn_model")
-
- else:
- # 如果不是训练,我们就去进行预测测试集数据
- for i in range(100):
- # 每次拿一个样本预测
- mnist_x, mnist_y = mnist.test.next_batch(1)
- print("第%d个样本的真实值为:%d, 模型预测结果为:%d" % (
- i+1,
- tf.argmax(sess.run(y_true, feed_dict={x: mnist_x, y_true: mnist_y}), 1).eval(),
- tf.argmax(sess.run(y_predict, feed_dict={x: mnist_x, y_true: mnist_y}), 1).eval()
- )
- )
-
- return None
-
-
- if __name__ == "__main__":
- full_connected_mnist()

参考文章:卷积神经网络超详细介绍-CSDN博客
参考文章:卷积神经网络—感受野与特征图_特征图越大,对检测效果有什么影响-CSDN博客
参考文章:卷积神经网络中卷积层、池化层、全连接层的作用_池化层作用-CSDN博客
池化层图片来自:卷积神经网络概念与原理_卷积神经网络原理-CSDN博客
参考文章:CNN笔记:通俗理解卷积神经网络_cnn卷积神经网络-CSDN博客
参考文章:神经网络——最易懂最清晰的一篇文章-CSDN博客



