TSNE——目前最好的降维方法

转自：http://blog.csdn.net/u012162613/article/details/45920827

1.流形学习的概念

流形学习方法(Manifold Learning)，简称流形学习，自2000年在著名的科学杂志《Science》被首次提出以来，已成为信息科学领域的研究热点。在理论和应用上，流形学习方法都具有重要的研究意义。

假设数据是均匀采样于一个高维欧氏空间中的低维流形，流形学习就是从高维采样数据中恢复低维流形结构，即找到高维空间中的低维流形，并求出相应的嵌入映射，以实现维数约简或者数据可视化。它是从观测到的现象中去寻找事物的本质，找到产生数据的内在规律。

以上选自百度百科

简单地理解，流形学习方法可以用来对高维数据降维，如果将维度降到2维或3维，我们就能将原始数据可视化，从而对数据的分布有直观的了解，发现一些可能存在的规律。

官方代码思想是一遍聚类一遍降维，其实也是一种比较好的自动聚类方法。

高维数据每个数据点被认为是一种正太分布数据（正太有三好），低维数据同样，然后让高维数据和低维数据相似度最大。又因为t分布好算而且和正太分布逼近，所以用了t分布来算就成了tsne方法。

2.流形学习的分类

可以将流形学习方法分为线性的和非线性的两种，线性的流形学习方法如我们熟知的主成份分析（PCA），非线性的流形学习方法如等距映射（Isomap）、拉普拉斯特征映射（Laplacian eigenmaps，LE）、局部线性嵌入(Locally-linear embedding，LLE)。

当然，流形学习方法不止这些，因学识尚浅，在此我就不展开了，对于它们的原理，也不是一篇文章就能说明白的。对各种流形学习方法的介绍，网上有一篇不错的读物（原作已找不到）：流形学习 (Manifold Learning)

3.高维数据降维与可视化

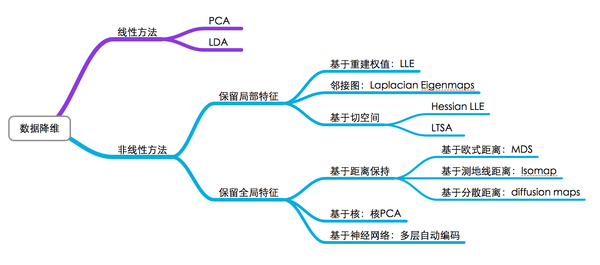
对于数据降维，有一张图片总结得很好（同样，我不知道原始出处）：

这里写图片描述

图中基本上包括了大多数流形学习方法，不过这里面没有t-SNE,相比于其他算法，t-SNE算是比较新的一种方法，也是效果比较好的一种方法。t-SNE是深度学习大牛Hinton和lvdmaaten（他的弟子？）在2008年提出的，lvdmaaten对t-SNE有个主页介绍：tsne,包括论文以及各种编程语言的实现。

接下来是一个小实验，对MNIST数据集降维和可视化，采用了十多种算法，算法在sklearn里都已集成，画图工具采用matplotlib。大部分实验内容都是参考sklearn这里的example，稍微做了些修改。

Matlab用户可以使用lvdmaaten提供的工具箱: