二叉树中的深搜_完全二叉树的深搜

一)计算布尔二叉树的值:深度优先遍历

2331. 计算布尔二叉树的值 - 力扣（LeetCode）

1)计算布尔二叉树需要从叶子节点向上进行计算，从下向上进行计算

2)完整二叉树是同时拥有左孩子和右孩子，或者是只有左孩子而完全没有右孩子

3)从宏观的角度来看待问题:发现重复子问题，当只盯着根节点来看的时候，此时我想知道我这一层的结果是什么？必须先知道这个根节点的左子树的布尔值，还需要知道右子树的布尔值，当我知道左右子树是true或者是false的时候，在我这一层把左右子树的信息整合，从而计算着这一颗二叉树的boolean值，从而返回上一层；

4)如果想要知道左子树或者是右子树是true还是false，这不是恰好和我们的大问题是一样的吗？主问题就是解决这棵树是true还是false

5)重复子问题函数头:给定一个指针，判断以这个指针为结点的树是true还是false，求以这个节点为根节点的boolean值；

6)函数体:先知道左子树是true还是false，再知道右子树是true还是false最后在本层进行整合

boolean flag1=dfs(root.left)；

boolean flag2=dfs(root.right)；

return root.val==2?flag1orflag2:flag1&flag2

7)递归出口:不能再次进行递归，遇到叶子节点，只需要将叶子节点是true还是false返回

8)从细节角度看待dfs:本质上这个题就是在做一个后序遍历，本质上就是一个深度优先遍历，先返回左节点的boolean值，再返回右节点的boolean值，最后再根据根结点的值进行计算，在遇到叶子节点的时候，将叶子节点的信息返回到上一层；

class Solution {
    public boolean evaluateTree(TreeNode root) {
    if(root==null) return true;
    if(root.left==null&&root.right==null) return root.val==0?false:true;
//先进行计算左子树的boolean值
        boolean flag1=evaluateTree(root.left);
//再进行计算右子树的boolean
        boolean flag2=evaluateTree(root.right);
        return root.val==2?flag1|flag2:flag1&flag2;
    }
}

二)求根节点到叶子节点数字之和

129. 求根节点到叶节点数字之和 - 力扣（LeetCode）

1)二叉树的递归问题想一下递归到某一层的时候要干什么事情，当遍历到某一个根节点所干的事情都一样的时候，况且干这个事情能够得到最终我所想要的结果，那么这个这个事情就是相同子问题，当我们遍历到某一个根节点的时候，还是需要将这个跟跟节点的左子树之和和右子树之和计算相加返回给上一层

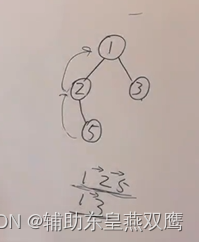
2)此时我们需要进行计算的点就是当遍历到某一个根节点的时候，需要知道前面的数字的信息，就比如说遍历到5的时候是需要知道12的信息的，因为当前我遍历到这一层的时候我什么也不知道，我怎么计算出1258呢？我只是知道当前根节点以及后续节点的信息，根本不知道当前根节点以前的信息，所以必须要把这个根节点之前的路径和给我

3)知道12的信息之后，再结合当前根节点进行计算出125的值，然后再将125传递给它的左子树和右子树，算出左右子树的值，最后将对应的值返回给根节点，在进行相加，返回到上一层节点

第一步:知道前面的数是12之后，进行计算当前结点的值是125 

第二步:将当前的这个125传递给以5为根节点的左子树，算出左子树的和是1258

第三步:将这个125传递给以5为根节点的右子树，计算出右子树的和是XXXX

第四步:将左子树和右子树返回的和进行相加，最后返回当前根节点的上一层

1)函数头的设计:传入一个根节点之后，把以这个根节点相连的左右子树叶子之和进行返回，int dfs(Node root，int k)，参数是当前传入的根节点和你传递到这个根节点的时候，从原始根节点到这个递归层次的结点的路径和，传入一个根节点，计算出以当前根节点的所有叶子节点之和进行返回

2)函数体:执行1 2 3 4步，先计算一下这个数，再求左子树的路径之和，再求右子树的路径之和，最后返回他们俩的和即可

3)递归出口:递归出口是在第二步进行执行的

左子树为空，或者是右子树为空，

class Solution {
    public int GetSum(TreeNode root,int k){
        //根据题目给定的数据范围来说不可能出现根节点的情况
        //遍历到叶子结点的时候才到了递归结束的出口
        if(root.left==null&&root.right==null){
            return root.val+k*10;
        }
        int current=k*10+root.val;
        int ret=0;
        //算出左子树的和
        if(root.left!=null) ret+=GetSum(root.left,current);
        //算出右子树的和
        if(root.right!=null) ret+=GetSum(root.right,current);
        //返回值是左子树和右子树的和
        return ret;
    }
    public int sumNumbers(TreeNode root) {
           return GetSum(root,0);
    }
}

三)二叉树剪枝:通过决策树抽象出递归的重复子问题

814. 二叉树剪枝 - 力扣（LeetCode）

1)在这个问题中子问题就是给定一个头指针，将以这个头指针为根节点的所有为0的子树全部干掉，返回最后处理结果的头指针，从下向上进行处理

2)当给定一个头结点的信息的时候，判断当前根节点是否删除，是否可以干掉当前的根节点的数，必须知道以当前根节点的左子树的信息和以当前根节点的右子树的信息，必须是左子树全为0或者是右子树全为0，我才可以将左子树或者是右子树剪掉，所以需要后序遍历，因为只有出现后序遍历的时候，才能向上着左子树的信息和右子树的信息；

3)进行模拟递归的过程:从叶子节点开始判断，通过决策树模拟删除递归的这样一个过程即可

1)当判断完左子树之后，我需要继续进行判断右子树也就是0的右节点，此时发现右节点的左子树和右子树也都是空，况且右节点的值也是0，所以右节点也是可以干掉的，但是此时返回到1的时候虽然发现左节点和右节点都是空，但是发现当前根节点是1，所以不能干掉

2)接下来继续判断0的右节点

3)函数体:先处理左子树，再进行处理右子树，再来处理当前节点

4)函数出口:root=null，直接不用处理

class Solution {
    //给定一个根节点,返回左子树和右子树简直之后的头节点
    public TreeNode pruneTree(TreeNode root) {
        if(root==null) return null;
        root.left=pruneTree(root.left);
//返回左子树剪枝之后的结果,将左子树中是0的分支全部干掉,返回处理完成之后的左根节点
        root.right=pruneTree(root.right);
//返回右子树剪枝之后的结果,将右子树是的0的分支全部干掉,返回处理之后的右根节点
        //判断当前位置是否需要剪枝,如果发现左右子树都为空，况且当前节点是0,那么直接返回即可
        if(root.left==null&&root.right==null&&root.val==0){
            return null;
        }else{
            return root;
        }
    }
}

四)验证二叉搜索树

98. 验证二叉搜索树 - 力扣（LeetCode）​​​​​​

之前我的做题思路就是说先进行判断一下以当前节点为根节点的左子节点和右子节点是一颗二叉搜索树，再进行判断当前根节点的左子树是否是一颗二叉搜索树，和当前根节点的右子树是否是一颗二叉搜索树，但是这个判断方法是错误的，只能通过72个测试用例，请看上面

解法1:根据中序遍历的结果来判断这颗树是否是二叉搜索树

class Solution {
    public List<Integer> GetList(TreeNode root){
        Stack<TreeNode> stack=new Stack<>();
        List<Integer> list=new ArrayList<>();
        while(!stack.isEmpty()||root!=null){
            while(root!=null){
                stack.push(root);
                root=root.left;
            }
            TreeNode node=stack.pop();
            list.add(node.val);
            root=node.right;
        }
        return list;
    }
    public boolean isValidBST(TreeNode root) {
        List<Integer> list=GetList(root);
        for(int i=0;i<list.size()-1;i++){
            if(list.get(i)>=list.get(i+1)) return false;
        }
        return true;
 
    }
}

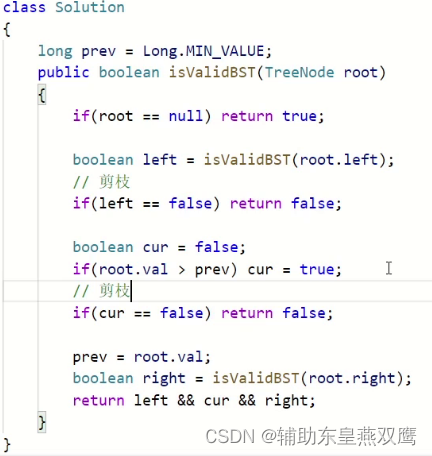
解法2:递归

左子树是一颗二叉搜索树，右子树是一颗二叉搜索树，当前节点符合二叉搜索树的定义

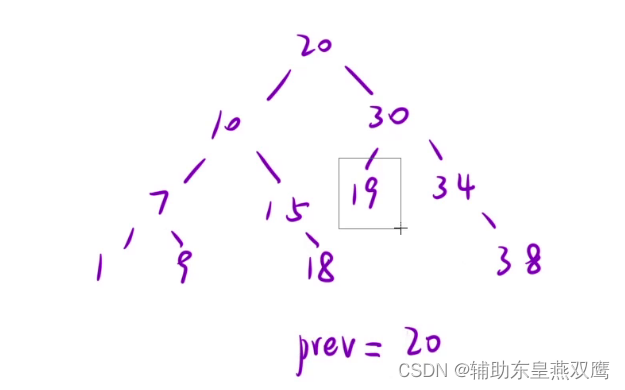
1)首先定义一个全局变量，prev=-00，这个全局变量的意思就是在中序遍历的过程中，当进行遍历到某一个位置的时候，它的中序遍历到此位置的前驱是多少，所以仅仅需要将当前位置的节点和它的前驱节点prev进行判断一下即可，prev的作用就是当进行中序遍历到某一个节点的时候，它的前驱的值是多少；

2)剪枝:就比如说在下面这个节点中，当我遍历到19这个位置的时候发现prev=20，此时就可以直接判断这棵树不是一个二叉搜索树了，那么应该此时直接停止中序遍历，直接向上返回false，当我们在深度优先遍历的过程中，发现某一个分支绝对不存在想要的结果的时候，在本题中发现这个分支不需要在进行遍历了，如果这个分支特别长，就可以剪掉很多枝叶了，就可以加快我们的搜索过程，就是为了避免深度优先遍历一些没有意义的东西

3)左子树是一颗二叉搜索树，当前节点也是符合二叉搜索树的定义，右子树也是一颗二叉搜索树， 根据当前节点如何来进行判断呢，只需要和prev作比较即可，无序和后面的数进行比较，因为和后面的数作比较的过程中序遍历已经帮助我完成了

class Solution {
    long prev=Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        if(root==null) return true;
boolean flag1=isValidBST(root.left);//先把判断左子树是否是一颗二叉搜索树
        boolean flag3=true;
        if(root.val<=prev) flag3= false;
 
       prev=root.val;
boolean flag2=isValidBST(root.right);//判断右节点是否是一颗二叉搜搜书
       return flag1&&flag2&&flag3;//如果左子树满足二叉搜索树定义,右子树满足二叉搜索树定义,况且根节点也满足二叉搜锁树定义,直接返回true
    }

五)二叉搜索树中第k小的元素

方法1:递归

230. 二叉搜索树中第K小的元素 - 力扣（LeetCode）

两个全局变量+中序遍历:

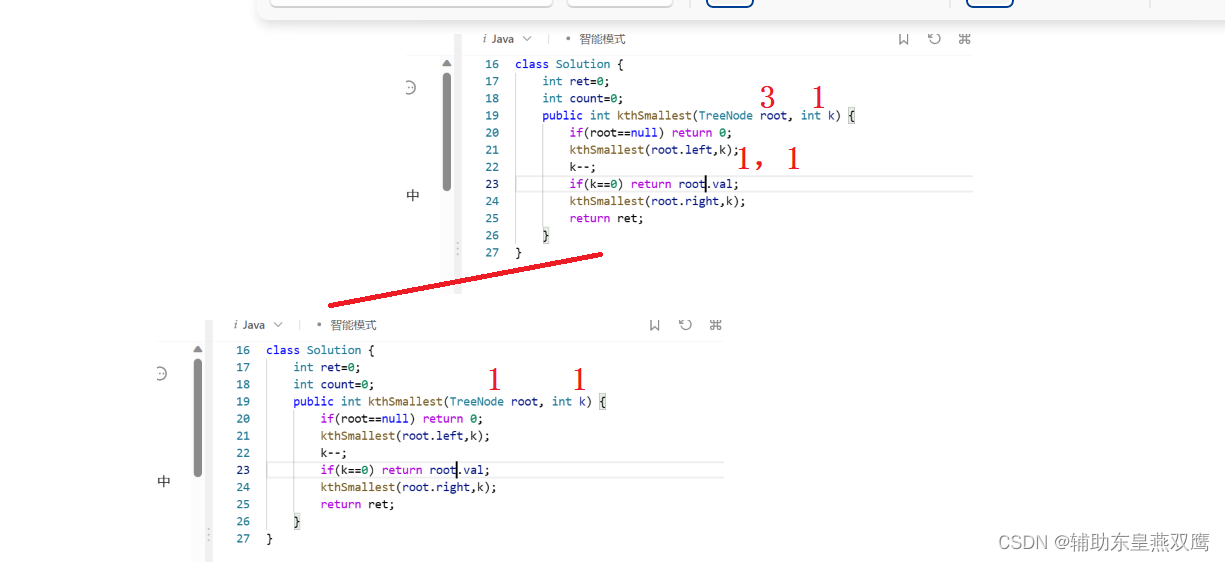
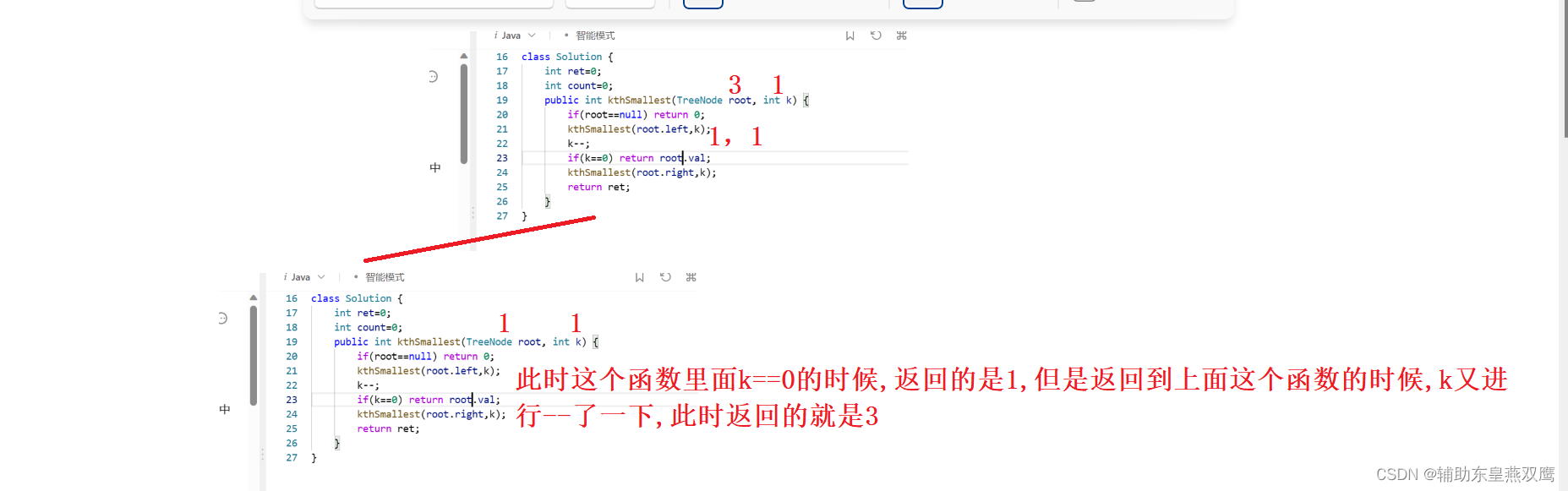
使用一个全局变量count，count=k，当k最终减到0的时候，使用另一个全局变量ret来保存最终返回的结果

class Solution {
    int ret=0;
    int count=0;
    public int kthSmallest(TreeNode root, int k) {
        count=k;
        dfs(root);
        return ret;
    }
    public void dfs(TreeNode root){
        if(root==null) return;
        dfs(root.left);
        count--;
        if(count==0){
            ret=root.val;
        }
        dfs(root.right);
    }
}

自己写一下，k当作是局部变量进行传递一定是存在问题的，

方法2:通过迭代的方式来遍历

class Solution {
    int ret=0;
    int count=0;
    public int kthSmallest(TreeNode root, int k) {
         Stack<TreeNode> stack=new Stack<>();
         while(!stack.isEmpty()||root!=null){
             while(root!=null){
                 stack.push(root);
                 root=root.left;
             }
             TreeNode node=stack.pop();
             k--;
             if(k==0){
                 return node.val;
             }
             root=node.right;
         }
         return -1;
    }
}

六)二叉搜索树中第k大的元素

解法1:递归+全局变量

class Solution {
    int ret=0;
    int count=0;
    public int kthLargest(TreeNode root, int k) {
         count=k;
         dfs(root);
         return ret;
    }
    public void dfs(TreeNode root){
        if(root==null) return;
        dfs(root.right);
         count--;
         if(count==0){
            ret=root.val;
        }
    
       dfs(root.left); 
    }
}

解法2:迭代

class Solution {
    public int kthLargest(TreeNode root, int k) {
        Stack<TreeNode> stack=new Stack<>();
        while(!stack.isEmpty()||root!=null){
            while(root!=null){
                stack.push(root);
                root=root.right;
            }
            TreeNode node=stack.pop();
             k--;
             if(k==0) return node.val;//不确定顺序可以使用节点计算一下
             root=node.left;
        }
    return -1;
    }
}

七)二叉树的所有路径:

这个题一定是需要使用前序遍历来进行遍历的，因为只有使用前序遍历，才能让他的父亲节点去指向孩子节点，这样才可以把路径完全输出出来

这个题中涉及到了回溯，那么具体是如何涉及到回溯的呢?比如说我们现在收集所有路径，现在收集路径收集到了1 2 5，那么当我们返回到上一层的时候需要将5给去掉，再次返回到上一层的时候需要将1给干掉，然后从根节点的右子树进行遍历

257. 二叉树的所有路径 - 力扣（LeetCode）

递归+全局变量:

恢复现场:当在进行深度优先遍历的过程中，是会进行更改这个全局变量的，那么当我回退到上一层的时候，我们要将这个全局变量回溯到上一层这个全局变量之前的样子；

1)从根节点开始，一直向下进行搜索，然后一边搜索的时候一边记录一下路径，到叶子节点找到了一个路径，使用叶子节点来存放一下路径即可，只需要存放到一个数组中返回即可；

2)第一个全局变量是一个字符串数组，里面存放的是一个字符串，当我在进行遍历的过程中，发现如果root遍历到了一个叶子节点，就向字符串数组里面塞；

3)来一个字符串全局变量path来记录当前遍历过的路径，作用就是当我们进行深度优先遍历的时候来记录一下路径

4)从根节点进行遍历，当遍历到非叶子节点的时候就更新path是数->

到叶子节点的时候，只添加一个叶子结点的值即可，不需要添加->，因为此时遇到叶子节点了，所以可以将这个字符串完整的加入到字符串数组里面，所以这个变量就是当我们进行深度优先遍历的时候，记录一下路径，当遍历到叶子结点的时候直接拼接上数字放到数组里面，如果不是叶子节点，拼接上数字->直接继续遍历

5)但是当遍历到叶子结点的时候，回溯的时候，是需要恢复现场的，反正还是需要进行pop操作和remove操作，况且当回溯到上一层结点的时候，如果是叶子节点只需要干掉一个数，但是非叶子节点向上回溯的过程中干掉的可是一个数和->所以操作是特别麻烦，所以恢复现场特别麻烦，所以使用全局变量不好用；

6)函数头:void dfs(TreeNode root，String path)，此时我们使用的这个递归函数的归的特性就可以自动帮助我们完成恢复现场的这个操作

7)这个题肯定是用前序遍历来做的，处理完左边回溯到根节点，然后再处理一下右边

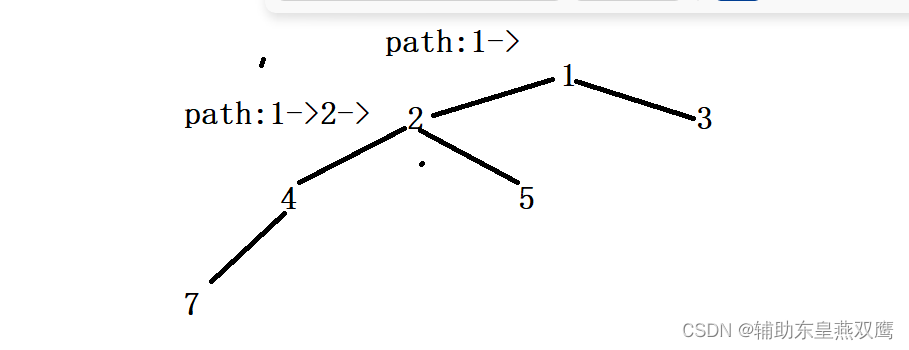
仔细来看我们的函数头，当我们在第一层的时候创建了一个全局变量path是1->，但是当遍历到第二层的时候，这个path在参数中重新创建了一个path变量就变成了1->2->，当把这一层东西搞定的时候，就不需要恢复现场了，函数本身已经帮助我们完成了恢复现场的操作

8)这是关心某一层在干啥，是叶子节点，不是叶子节点，添加完成这个数之后，添加一下箭头，然后把这个path和root传递给左树和右数

9)剪枝操作:当我的左子树是空的时候，我就没有必要去左子树中去寻找路径了，因为左子树一定是不存在我们最终想要的结果的，同理右子树也是一样的道理；

class Solution {
    List<String> list=new ArrayList<>();
    public void dfs(TreeNode root,String path){
        if(root==null) return;
        if(root.left==null&&root.right==null){
            list.add(path+root.val);
            return;
        }
    dfs(root.left,path+root.val+"->");
    dfs(root.right,path+root.val+"->");
    }
    public List<String> binaryTreePaths(TreeNode root) {
        dfs(root,"");
        return list;
    }
}

当进行深度优先遍历的时候，先是从根节点一直向下走，从而模拟一下拼接字符串的过程

8)剪枝操作:当左子树是空的时候，就不需要进行dfs(root.left)，同时当右子树为空的时候，也不需要dfs(root.right)

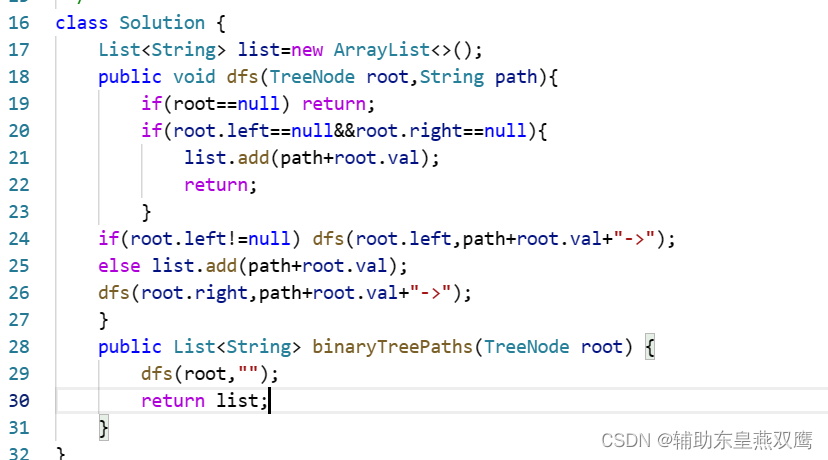
错误代码: