最长回文子序列

目录

一、前言

二、最长回文子序列

1、问题描述

2、基本思路

3、上题目链接

4、python题解代码

三、拓展模板题(我一开始是看这道题学的最长回文子序列)

1、上链接

2、基本思路

---

一、前言

对于学计算机的同学来说，学习算法是一件非常重要的事情，废话不多讲，我们来讲讲“最长回文子序列问题”。

二、最长回文子序列

1、问题描述

给定一个字符串，请你求出其中的最长回文子序列的长度。

输入：s = "bbbab"
输出：4
解释：一个可能的最长回文子序列为 "bbbb" 。

输入：s = "cbbd"
输出：2
解释：一个可能的最长回文子序列为 "bb" 。

2、基本思路

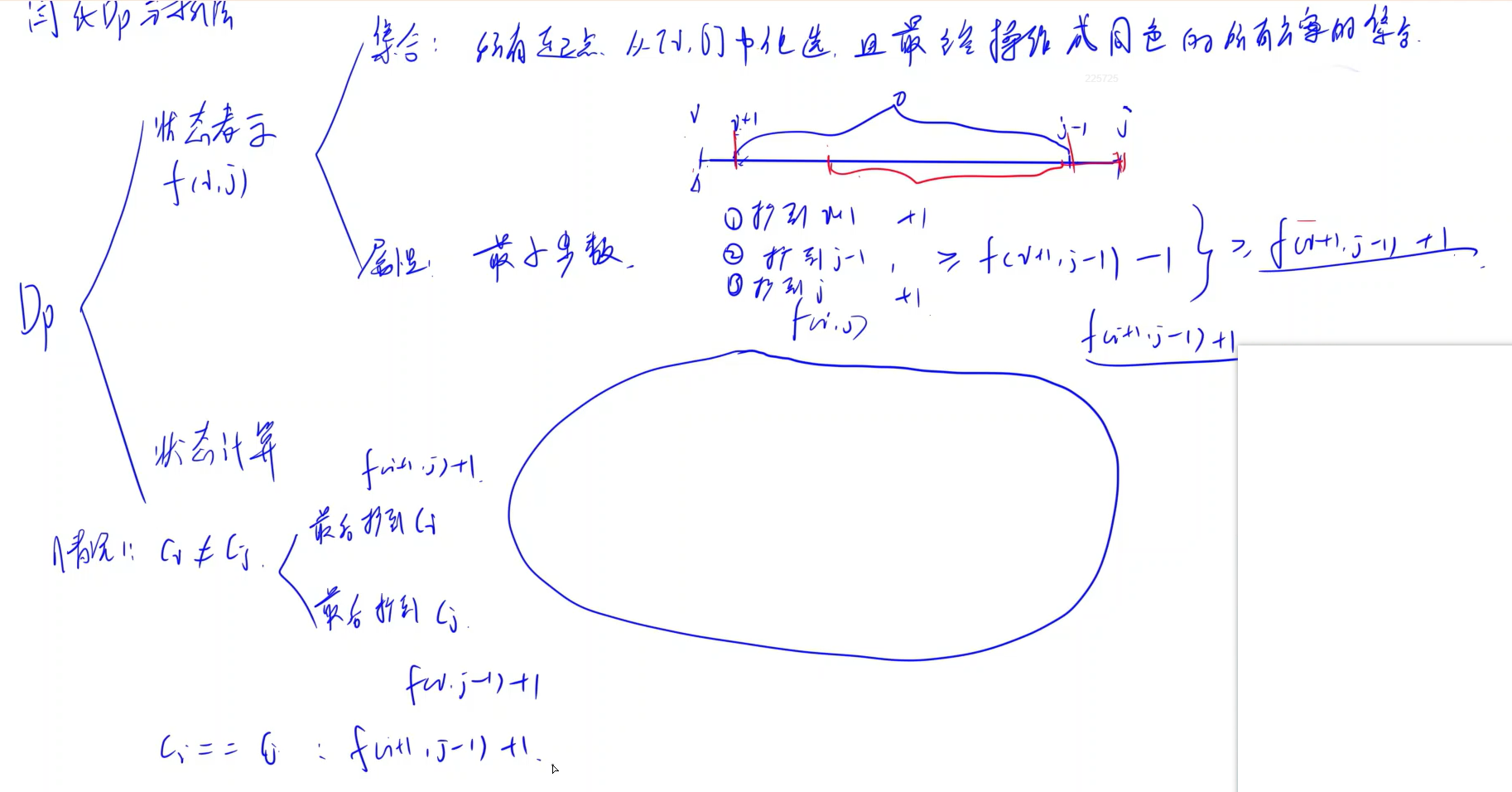
对于一个子序列而言，如果它是回文子序列，并且长度大于 2，那么将它首尾的两个字符去除之后，它仍然是个回文子序列。因此可以用区间dp的方法计算给定字符串的最长回文子序列。

下面引用力扣的解释：

用 dp[i][j] 表示字符串 s 的下标范围 [i, j] 内的最长回文子序列的长度。假设字符串 s 的长度为 n，则只有当 0 ≤ i ≤ j < n 时，才会有 dp[i][j]>0，否则 dp[i][j]=0。

由于任何长度为 1 的子序列都是回文子序列，因此动态规划的边界情况是，对任意 0≤i<n，都有 dp[i][i]=1。

当 i<j 时，计算 dp[i][j] 需要分别考虑 s[i] 和 s[j] 相等和不相等的情况：

• 如果 s[i] = s[j]，则首先得到 s 的下标范围 [i+1, j−1] 内的最长回文子序列，然后在该子序列的首尾分别添加 s[i] 和 s[j]，即可得到 s 的下标范围 [i,j] 内的最长回文子序列，因此
• dp[i][j] = dp[i+1][j−1] + 2；
• 如果 s[i]≠s[j]，则 s[i] 和 s[j] 不可能同时作为同一个回文子序列的首尾，因此
• dp[i][j] = max⁡(dp[i+1][j], dp[i][j−1])

由于状态转移方程都是从长度较短的子序列向长度较长的子序列转移，因此需要注意动态规划的循环顺序。

最终得到 dp[0][n−1] 即为字符串 s 的最长回文子序列的长度。

显然，转移方程里由于每次计算 dp[i][j] 需要用到 dp[i+1][j-1]、dp[i+1][j]、dp[i][j-1]这三个点，也就是左下、正下、左侧的值，因此每次计算需要确保左下，正下，正左已经计算好了，因此需要从右下角从左至右开始遍历（在初始化对角线为 1 和左侧三角范围为 0 后）

3、上题目链接

516. 最长回文子序列 - 力扣（Leetcode）

4、python题解代码

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        n=len(s)
        dp=[[0]*(n+2) for _ in range(n+2)]
        for i in range(n):
            dp[i][i]=1
 
        for i in range(n-1,-1,-1):
            for j in range(i+1,n):
                if s[i]==s[j]:
                    dp[i][j]=dp[i+1][j-1]+2
                else:
                    dp[i][j]=max(dp[i+1][j],dp[i][j-1])
 
        # print(dp[0][n-1])
        return dp[0][n-1]

三、拓展模板题(我一开始是看这道题学的最长回文子序列)

1、上链接

3996. 涂色 - AcWing题库

2、基本思路

代码见Acwing。

以上，最长回文子序列

祝好~