- 1redis 面经详解_面经 redis
- 2手动安装Spacy model的步骤_spacy-models
- 3windows服务器的基线安全(等保要求)_等保基线是什么
- 4源代码管理的另类比较:TortoiseGit vs SourceTree_sourcetree和小乌龟哪个好用
- 5Mac 虚拟机Parallels Desktop安装win7 、win10系统_parallels desktop 13安装win7
- 6ComfyUI-moondream
- 7python安装各种包_python安装包
- 8RadioGroup里RadioButton显示多行实现(非常简单)_c#radiogroup按钮一列显示
- 9c语言编程multiplies,C ++中的函数式编程
- 10cv2: imread & imwrite & imshow_cv2.imread hwc
FAST-LIO论文阅读_fastlio
赞
踩
各位大佬对论文的解析:
FAST-LIO论文解读与详细公式推导
FAST-LIO是港大MaRS实验室在2021年提出的一个紧耦合迭代扩展卡尔曼滤波高计算效率、高鲁棒性的雷达里程计。影响深远,后续又陆续提出了FAST-LIO2以及Faster-LIO等框架。
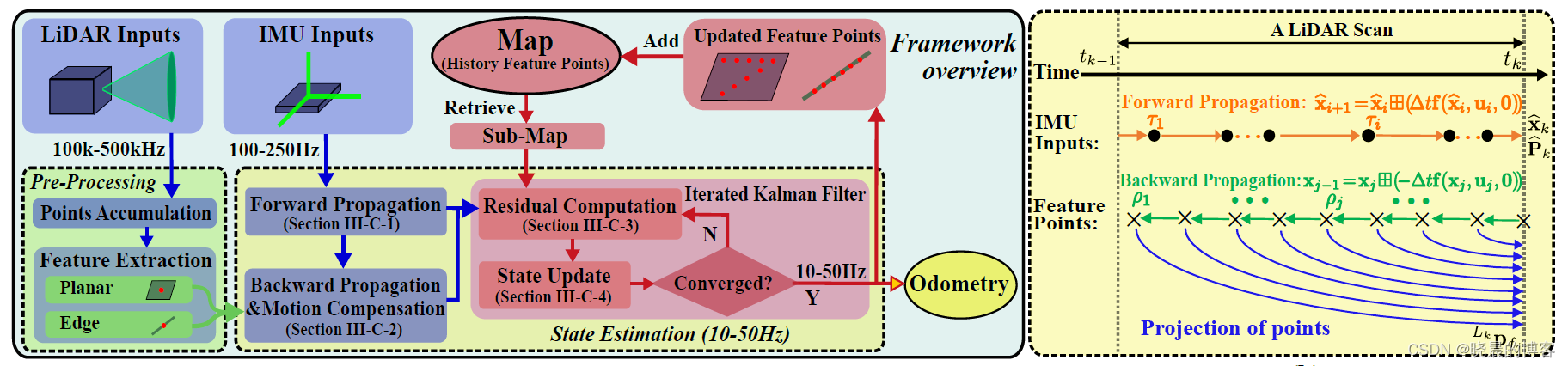
下面,我们简单了解一些论文中的各个模块及其处理流程。
符号说明

t
k
t_{k}
tk第K帧激光扫描的结束时间
τ
i
\tau_{i}
τiLiDAR扫描帧中的第i个IMU数据
ρ
j
\rho_{j}
ρjLiDAR扫描帧中的第j个激光点时间
I
i
,
I
j
,
I
k
I_{i},I_{j},I_{k}
Ii,Ij,Ik IMU在
τ
i
\tau_{i}
τi,
ρ
j
\rho_{j}
ρj,以及
t
k
t_{k}
tk三个时刻的载体坐标系
L
j
,
L
k
L_{j},L_{k}
Lj,Lk LiDAR在
ρ
j
\rho_{j}
ρj,
t
k
t_{k}
tk时刻的激光坐标系。
X
,
X
^
,
X
ˉ
X,\hat{X}, \bar{X}
X,X^,Xˉ:状态X的真值,预测值,更新值(后验,估计值)
X
~
\tilde{X}
X~:状态X的真值
X
X
X与估计值
X
ˉ
\bar{X}
Xˉ之间的误差(即:
X
~
=
X
⊟
X
ˉ
\tilde{X}=X\boxminus\bar{X}
X~=X⊟Xˉ ,
X
=
X
~
⊞
X
ˉ
X=\tilde{X}\boxplus\bar{X}
X=X~⊞Xˉ )
X
^
κ
\hat{X}^\kappa
X^κ:迭代扩展卡尔曼滤波(IEKF)中的第
κ
\kappa
κ次迭代的状态量
X
i
,
X
j
,
X
k
X_{i},X_{j},X_{k}
Xi,Xj,Xk:在
τ
i
\tau_{i}
τi,
ρ
j
\rho_{j}
ρj,以及
t
k
t_{k}
tk三个时刻的状态量
X
ˇ
j
\check{X}_{j}
Xˇj:在后向传播中,相对于
t
k
t_{k}
tk时刻状态
X
k
X_{k}
Xk的估计值
X
j
X_{j}
Xj
基础概念(运算符)
作者在文中定义了两个基础的运算符,
⊞
\boxplus
⊞与
⊟
\boxminus
⊟。
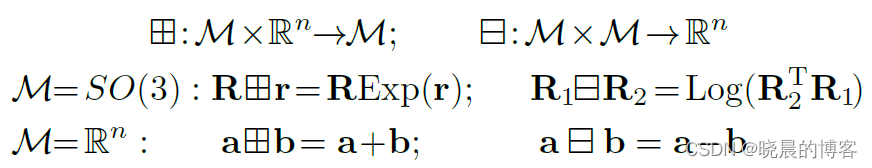
这里的
M
M
M表示一种
n
n
n维的流形。
⊞
\boxplus
⊞操作对应于在流形
M
M
M上增加一个小的扰动。
⊟
\boxminus
⊟操作对应于两个流形
M
1
M_1
M1与
M
2
M_2
M2之间的微小差值。
分别对应于指数映射与对数映射。
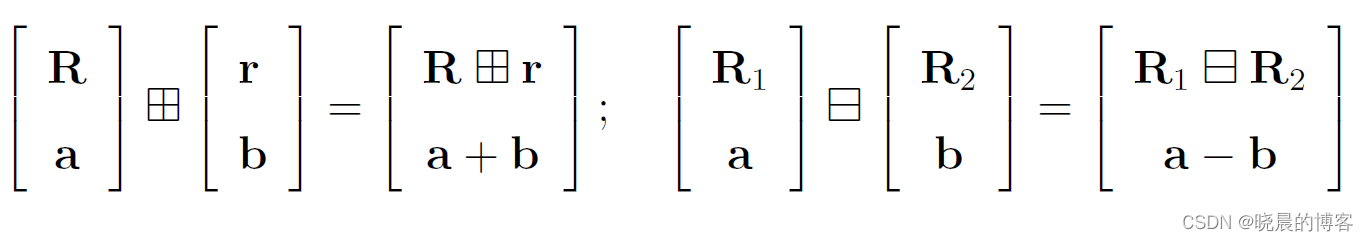
同时,我们可以推导出下述结论

文中以IMU坐标系作为载体系,推出来的位姿也在载体系中。假设激光雷达与IMU刚性链接,使用一个外参转换关系 I T L = ( I R L , I p L ) {^I}T{_L}=({^I}R{_L}, {^I}p{_L}) ITL=(IRL,IpL)进行转换。
IMU连续模型
IMU的动力学模型如下:

这是易于理解的,位置的导数是速度,速度的导数为加速度(增加的坐标转换与重力影响),重力为一个常数,导数为0,旋转的导数为角速度(推导可以参考高翔博士的SLAM十四讲),陀螺仪与加速计零偏的导数为高斯白噪声。
IMU离散模型
假设,IMU的采样频率为 Δ t \Delta t Δt,则离散模型可以写成如下形式:
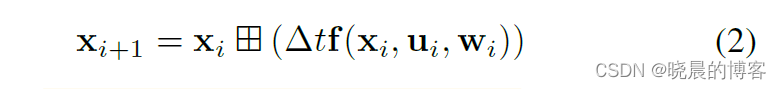
其中:
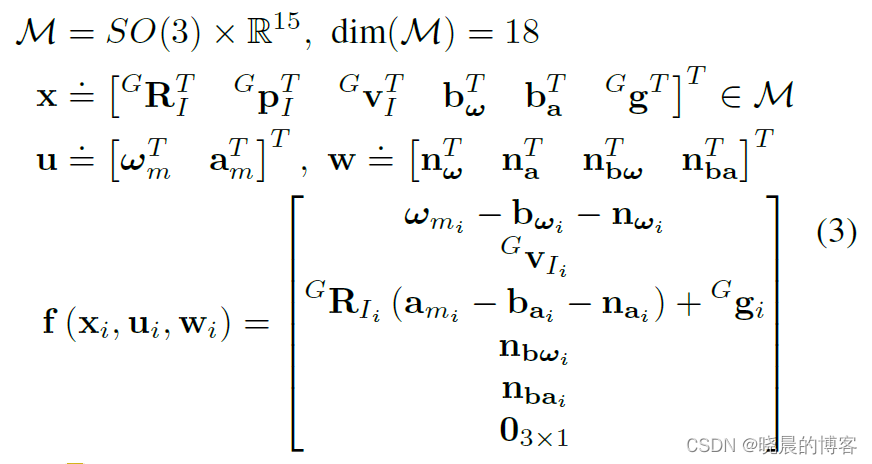
LiDAR帧的概念
实际工作过程中 LiDAR是在不断的连续扫描的(这个频率非常高,数十万Hz),但是我们为了能够处理点云数据,人为的划分成了不同的扫描帧,如文中把累积20ms的点云作为一帧数据,扫描频率为50Hz。
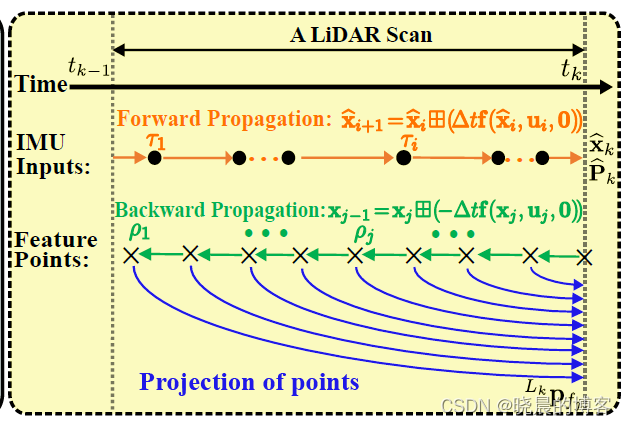
即把上图中
t
k
−
1
t_{k-1}
tk−1到
t
k
t_{k}
tk的时间段(20ms)划分为一帧点云。
但是,这样引起一个问题是,带来了运动畸变。对于这一问题,在后续的章节中通过后向传播来进行纠正。
状态估计
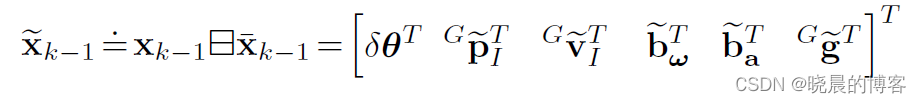
作者使用误差作为要估计的状态,这样做有一系列好处:参考高翔博士-简明ESKF推导
- 在旋转的处理上,ESKF的状态变量可以采用最小化的参数表达,也就是使用三维变量来表达旋转的增量。而传统KF需要用到四元数(4维)或者更高维的表达(旋转矩阵,9维),要不就得采用带有奇异性的表达方式(欧拉角)。
- ESKF总是在原点附近,离奇异点较远,并且也不会由于离工作点太远而导致线性化近似不够的问题。
- ESKF的状态量为小量,其二阶变量相对来说可以忽略。同时大多数雅可比矩阵在小量情况下变得非常简单,甚至可以用单位阵代替。
- 误差状态的运动学也相比原状态变量要来得更小,因为我们可以把大量更新部分放到原状态变量中。
前向传播(运动方程)
前向传播的执行过程如下,每次接收到一次数据我们就会执行一次。
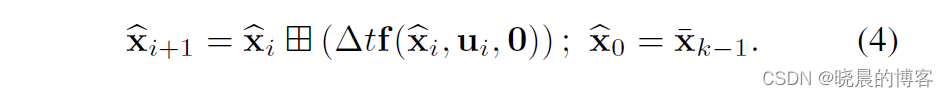
此外,由于不知道噪声的值,所以设置噪声 w w w为0,不断进行前向传播。当然,这样很快就会“飘”。但是,我们还有观测方程(LiDAR)进行修正。
对公式(4)转换为误差的形式,并进行线性化:

F
X
~
F_{\tilde{X}}
FX~与
F
W
F_{W}
FW分别为
X
~
i
+
1
\tilde{X}_{i+1}
X~i+1与
w
i
{w}_{i}
wi变量的雅克比矩阵。形式如下:
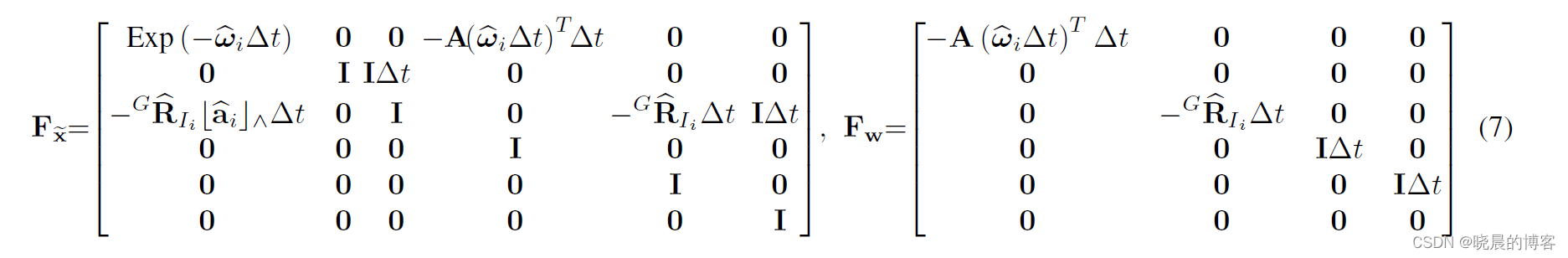
其中A(.)的表示方式为:
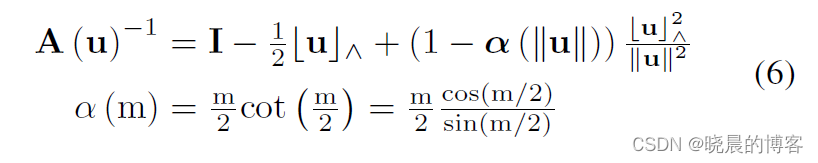
推导方式见论文中的附录,这里就不详细说了,很烦人。
有了运动方程的线性化表达式,我们还需要对应的协方差更新方式,假设噪声
w
w
w的协方差为
Q
Q
Q,则更新方式为:
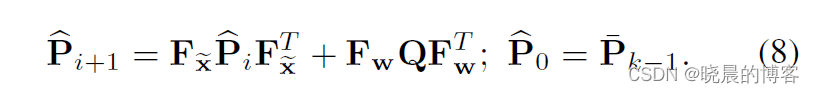
直到一帧的扫描终点时刻
t
k
t_k
tk,一个前向传播过程才结束。终点时刻
t
k
t_k
tk的预测状态表示为
X
^
k
\hat{X}_k
X^k,对应的协方差表示为
P
^
k
\hat{P}_k
P^k(状态预测值
X
^
k
\hat{X}_k
X^k与状态真值
X
k
{X}_k
Xk之间的误差的协方差
X
^
k
⊟
X
k
\hat{X}_k\boxminus{X}_k
X^k⊟Xk)。
后向传播(运动畸变校正)
我们在处理过程中会融合在 t k t_k tk时刻的状态 X ^ k \hat{X}_k X^k与协方差 P ^ k \hat{P}_k P^k。但是,正如我们之前所提到的,每个点都有属于他们自己的时间戳,其测量时间并不是我们所规定的 t k t_k tk时刻,即LiDAR点采样(测量)时间 ρ j < t k \rho_j<t_k ρj<tk,这会引起参考坐标系的不一致。

如图中的下半部分,为了消除这种影响,作者使用下述公式,反向(后向)从
t
k
t_k
tk时刻的位姿,推算出
ρ
j
\rho_j
ρj时刻的位姿,并把
ρ
j
\rho_j
ρj时刻的特征点转换到
t
k
t_k
tk时刻。
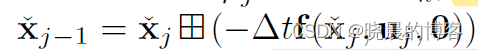
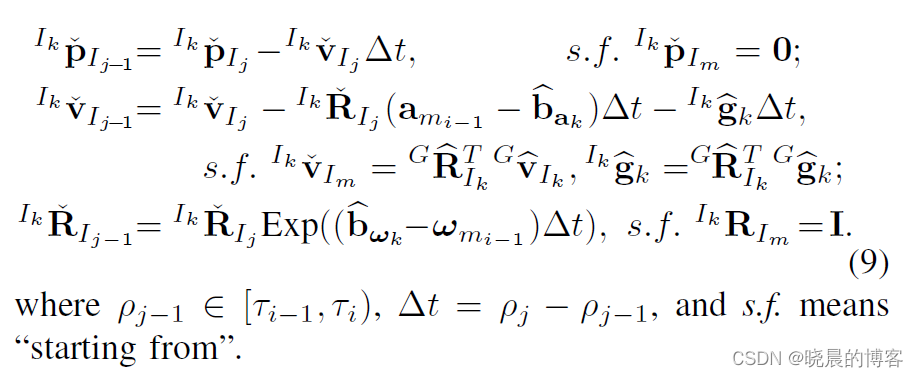
注意,因为特征点的频率高于IMU频率,所以并不是每个特征点时刻对应一个位姿。每个特征点的转换位姿都由其左侧的IMU时刻确定。
通过上述计算,得到 ρ j \rho_j ρj时刻到 t k t_k tk时刻的相对位姿为: I k T ˇ I j = ( I k R ˇ I j , I k p ˇ I j ) ^{I_k}{\check T}_{I_j}=(^{I_k}{\check R}_{I_j}, ^{I_k}{\check p}_{I_j}) IkTˇIj=(IkRˇIj,IkpˇIj)
基于此,我们可以通过下式,把局部坐标系的点测量值
L
j
p
f
j
^{L_j}{p}_{f_j}
Ljpfj,投影的扫描终点时刻
t
k
t_k
tk,即
L
k
p
f
j
^{L_k}{p}_{f_j}
Lkpfj。
L
k
p
f
j
=
I
T
L
−
1
I
k
T
ˇ
I
j
I
T
L
L
j
p
f
j
^{L_k}{p}_{f_j}={^{I}{T}^{-1}_{L}} {^{I_k}{\check T}_{I_j}} {^{I}{T}_{L}} {^{L_j}{p}_{f_j}}
Lkpfj=ITL−1IkTˇIjITLLjpfj
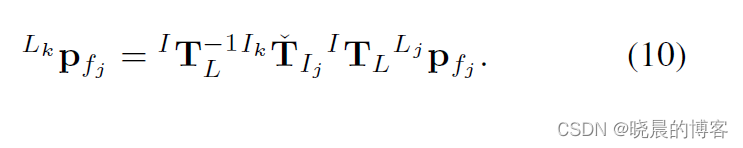
式中,
I
T
L
^{I}{T}_{L}
ITL为LiDAR与IMU之间的外参,
L
k
p
f
j
^{L_k}{p}_{f_j}
Lkpfj为投影到扫描终点时刻
t
k
t_k
tk的坐标,用于下面的残差计算。
残差计算
经过上节中的运动畸变校正,我们可以把一个扫描帧中的所有特征点视为在同一时刻
t
k
t_k
tk处进行采样,接着,投影到全局坐标系中:
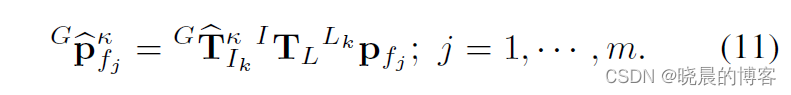
式中,
G
T
^
I
k
κ
{^{G}{\hat T}^{\kappa}_{I_k}}
GT^Ikκ为我们想要求的
t
k
t_k
tk时刻到全局坐标系下的位姿变换。
类似于LOAM的思想,转换后的特征点应该落在其对应的特征“线”“面”上,但是由于存在LiDAR测量误差与前向传播的状态推算误差,导致转换后的特征点并不能完全落在特征线/面上。
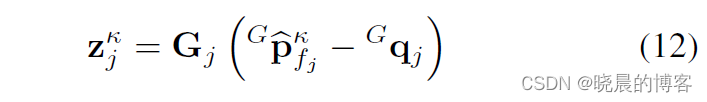
式中,
G
j
G_j
Gj为法向量
u
j
T
u^T_j
ujT(平面特征)或为边缘线特征朝向的反对称阵
⌊
u
j
⌋
∧
\left \lfloor u_j \right \rfloor_{\wedge }
⌊uj⌋∧(边缘特征)。即计算点到面或者点到线之间的距离。
作者只考虑模长小于0.5m的残差值。残差值高于阈值的被认为是噪声点或者是新观测的点。
迭代状态更新
如果我们把激光雷达的测量噪声去除,假设测量的点都是真实的坐标。
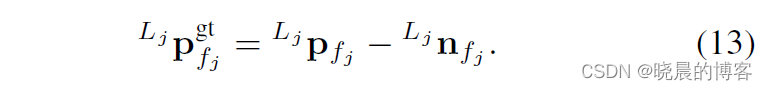
那么我们使用这个真值代入上述公式中转换的全局坐标系
G
G
G,再使用状态的真值
X
k
X_k
Xk(有变换的真值
G
T
I
k
{^{G}{T}_{I_k}}
GTIk),那么残差
z
j
κ
z^{\kappa}_j
zjκ的值应该为0;
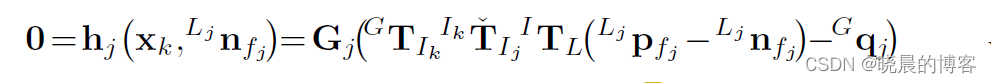
对上式
h
j
h_j
hj进行一阶近似:
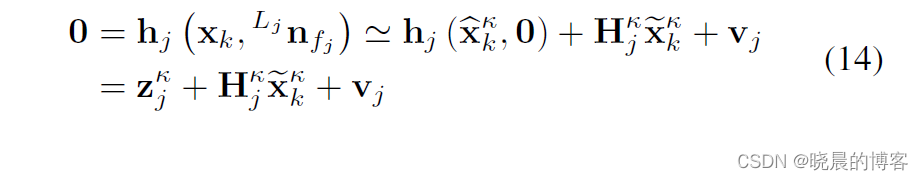
式中, X ~ k κ = X k ⊟ X ^ k κ \tilde{X}^{\kappa}_k=X_k\boxminus\hat{X}^{\kappa}_k X~kκ=Xk⊟X^kκ , X k = X ^ k κ ⊞ X ~ k κ X_k=\hat{X}^{\kappa}_k\boxplus\tilde{X}^{\kappa}_k Xk=X^kκ⊞X~kκ。
存在:
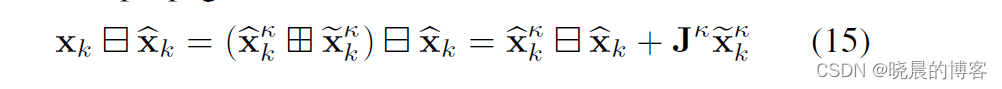
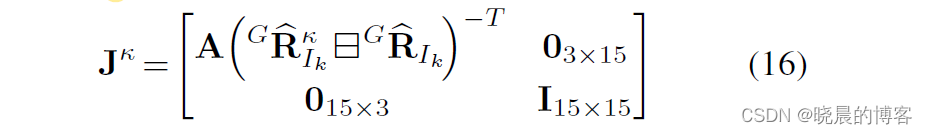
结合(15)(运动方程)及残差(14)(观测方程),我们得到下述形式的目标函数:
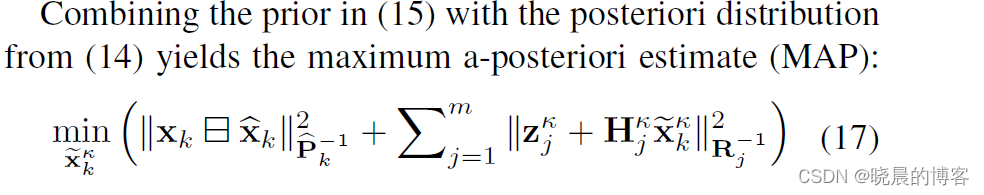
式中:
∥
x
∥
M
2
=
X
T
M
X
\left \| x \right \|^2_M=X^TMX
∥x∥M2=XTMX
利用迭代卡尔曼滤波,我们对(17)进行求解

得到 X ˉ k \bar{X}_k Xˉk与 P ˉ k \bar{P}_k Pˉk。
上述求解过程中还存在一个问题是求解卡尔曼增益K需要对 H P H T + R HPH^T+R HPHT+R进行求逆。这个维度为 m ∗ m m*m m∗m即特征点的数量(观测的数量)。这个维度是很大的,所以求解比较困难。
作者把卡尔曼增益的公式等价转换为下述形式,求逆的维度为状态量的维度
18
∗
18
18*18
18∗18,大大降低了计算的维度。
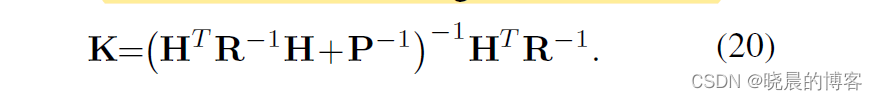
等价转换过程的推导也是比较简单的,利用了矩阵的求逆定理。



