二叉树顺序结构的实现_用顺序结构实现二叉树,如何考虑空值

1.堆的构建过程

首先来介绍一下堆的概念：
1.堆中的某个节点的值总是不大于或者不小于父节点的值；
2.堆总是一颗完全二叉树；

由概念可知堆的两种形态如下图所示

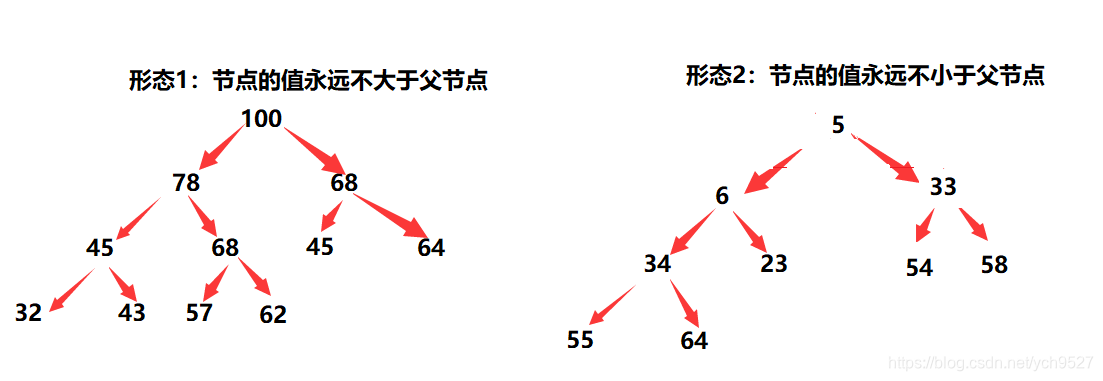
1.1堆的向下调整算法

比如，随机给出一个数组，逻辑上看做一颗完全二叉树，通过根节点开始向下调整算法可以将其调整成一个小堆(大堆)。需要注意的是使用向下调整算法需要左右子数必须是一个堆。

图文解析如下：

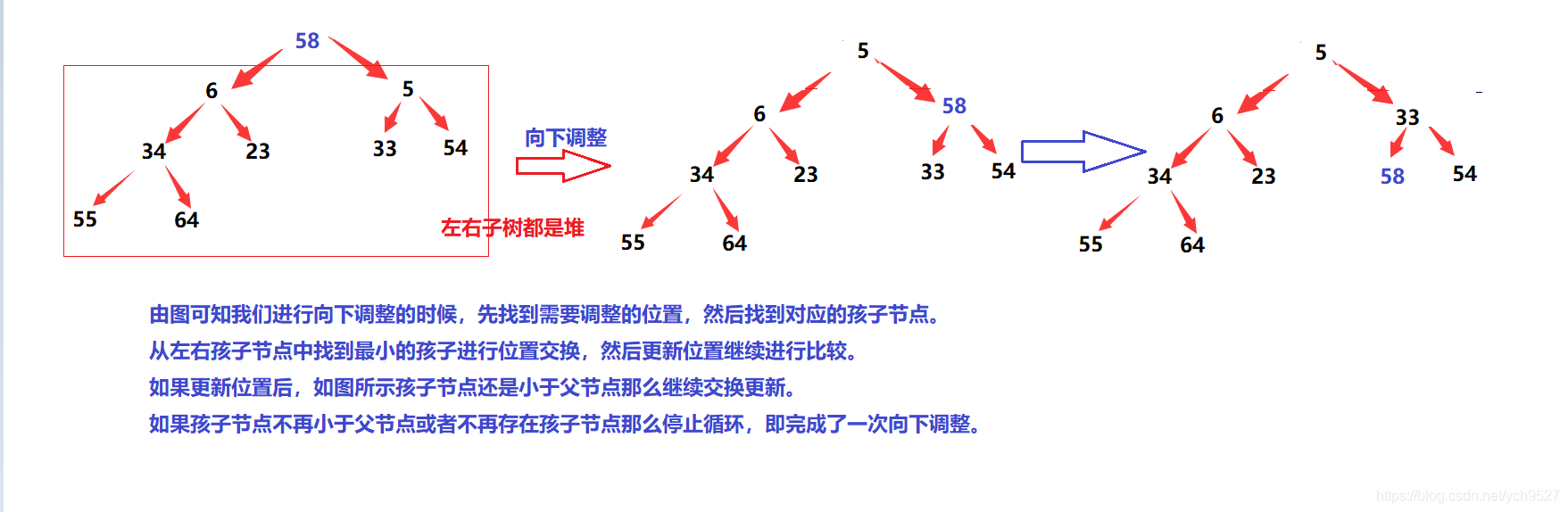
时间复杂度分析：
每次向下调整的次数为树的当前节点对应的高度，因此为O(logN);

实现代码：

void Swap(HPDataType *arr, int parent, int child)
{
	HPDataType temp = arr[parent];
	arr[parent] = arr[child];
	arr[child] = temp;
}

void ShiftDown(HPDataType *arr, int size, int parent)//堆向下进行调整
{
	int child = parent*2+1;//左孩子坐标
	while (child < size)
	{
		if (child + 1 < size&&arr[child + 1] < arr[child])//右孩子比左孩子小
			child++;
		if (arr[child] < arr[parent])//父节点比孩节点要大
		{
			Swap(arr,parent,child);//进行交换

			//节点更新
			parent = child;
			child = parent * 2 + 1;
		}
		else
			break; //父节点比孩节点小
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

1.2堆的构建

有上面我们知晓了堆的向下调整算法，但是这种算法要求左右子树必须是个对才能进行调整，我们应该如何进行呢？

我们可以在构建堆的时候，将数组看成一个完全二叉树，我们从最后一个非叶子节点开始调整，这样我们进行向下调整的时候就可以保证调节点的左右子树一直是一个堆，演示图如下：

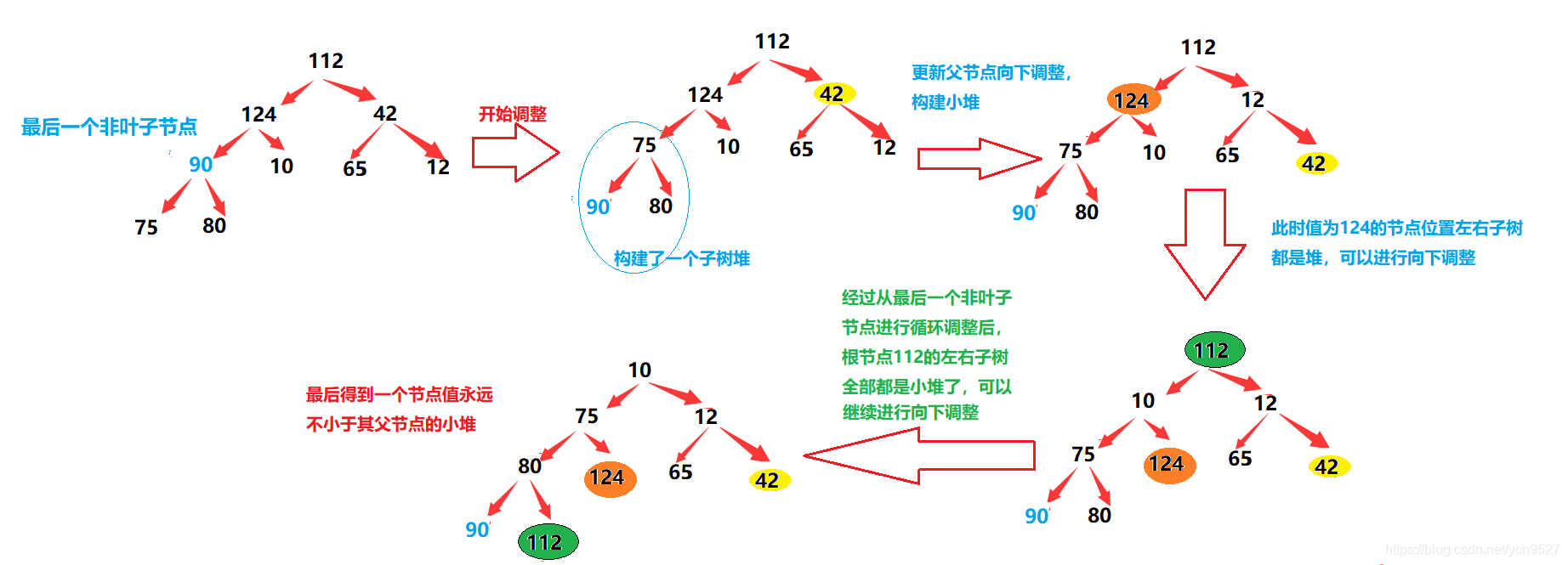
由上图可知，从最后一个叶节点开始，通过循环更新节点，向下调整构建小堆，一直循环到最后一个根节点时，其左右两边的子树全部都是小堆。因此可以进行向下调整，调整完成后即小堆构建完成；

时间复杂度分析：
第一层节点的个数为2^0个，单个节点向下调整的次数为h次
第二层的节点个数为2^1个，单个节点向下调整的次数为h-1次
第三层的节点个数为2^2个，单个节点的向下调整次数为h-2次
…
第h-1层的节点个数为2^(h-2)个，每个节点的向下调整次数为1次

即可求出：时间复杂度=2^0 * h+2^1 * (h-1)+2^2 * (h-2)+…+2^(h-2) * 1

通过h=logN和错位相减得到：时间复杂度=N-logN-2

即建堆的时间复杂度为：O(N)

实现代码

void heapCreate(Heap *hp, HPDataType *arr, int size)
{
	//进行堆数据的拷贝
	hp->arr = (HPDataType *)malloc(sizeof(HPDataType)*size);//开辟堆空间
	if (hp->arr == NULL)
		return;
	hp->capacity = hp->size = size;
	memcpy(hp->arr, arr, size*sizeof(HPDataType));

	//进行堆的排序，从最后一个非叶子节点开始
	int parent = (size - 2) / 2;//最后一个非叶子节点
	while (parent >= 0)
	{
		ShiftDown(hp->arr, size, parent);
		parent--;
	}

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

2.堆的插入和删除

2.1堆的插入

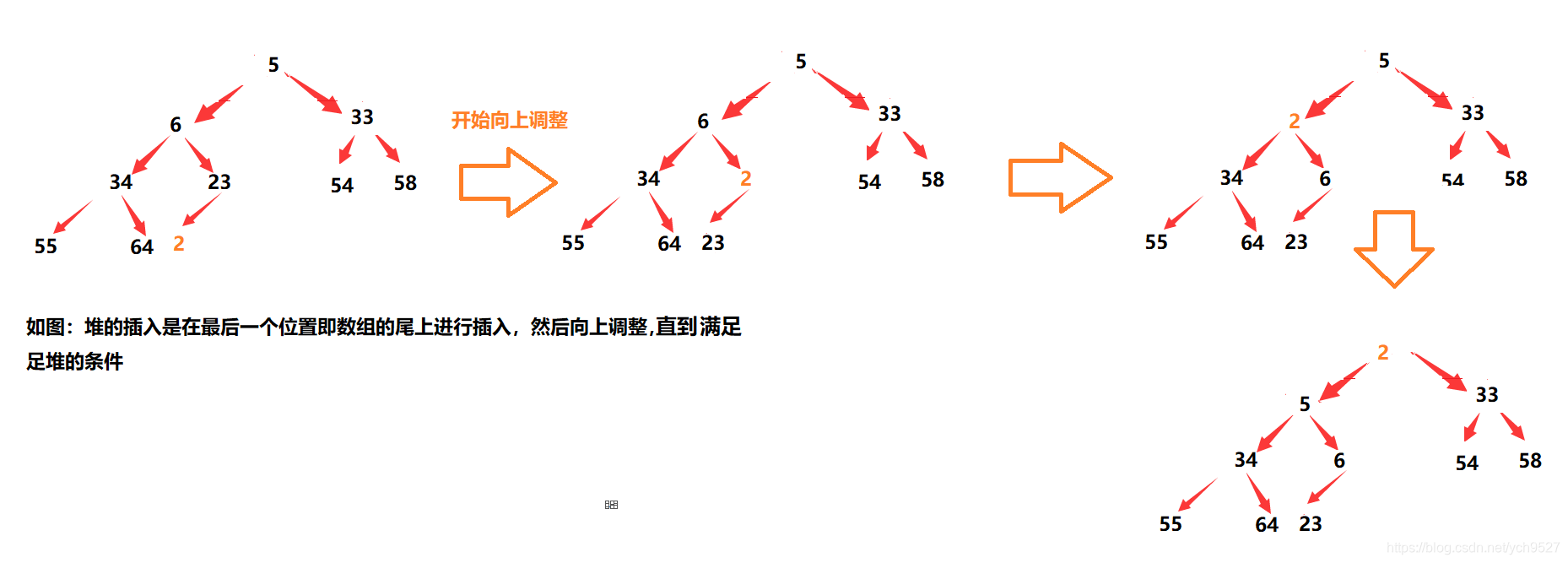
实现代码

void ShiftUp(HPDataType *arr,  int child)//向上调整
{
	int parent = (child - 1) / 2;
	while (child > 0)//有孩节点必定有父节点
	{
		if (arr[parent] > arr[child])
		{
			Swap(arr, parent, child);
			child = parent;
			parent = (child - 1) / 2;	
		}
		else
			break;
	}
}

void HeapPush(Heap *hp, HPDataType data)
{
	if (hp->size == hp->capacity)//空间容量判定
	{
		HPDataType *Node = (HPDataType *)malloc(sizeof(HPDataType)* 2 * hp->capacity);
		if (Node == NULL)
			exit(-1);
		hp->capacity = 2 * hp->capacity;
	}
	hp->arr[hp->size++] = data;
	ShiftUp(hp->arr,hp->size-1);

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

2.2堆的删除

将堆顶和队尾的数据进行交换，然后删除掉队尾，最后再进行向下排序，即完成了堆顶元素的删除；

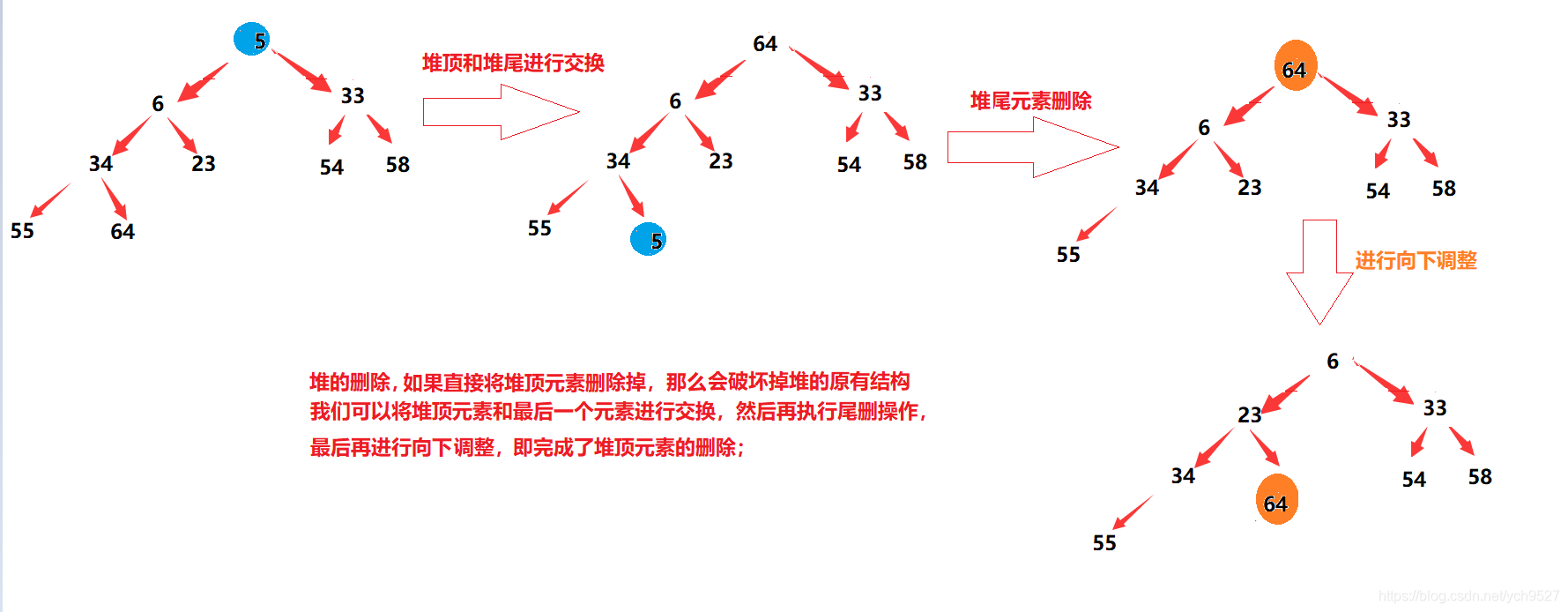
实现代码：

void HeapPop(Heap *hp)
{
	if (hp->size == 0)//为空
		return;

	Swap(hp->arr, 0, hp->size - 1);//交换
	hp -> size--;//删除
	ShiftDown(hp->arr, hp->size, 0);//向下调整
}
1
2
3
4
5
6
7
8
9

3.排序

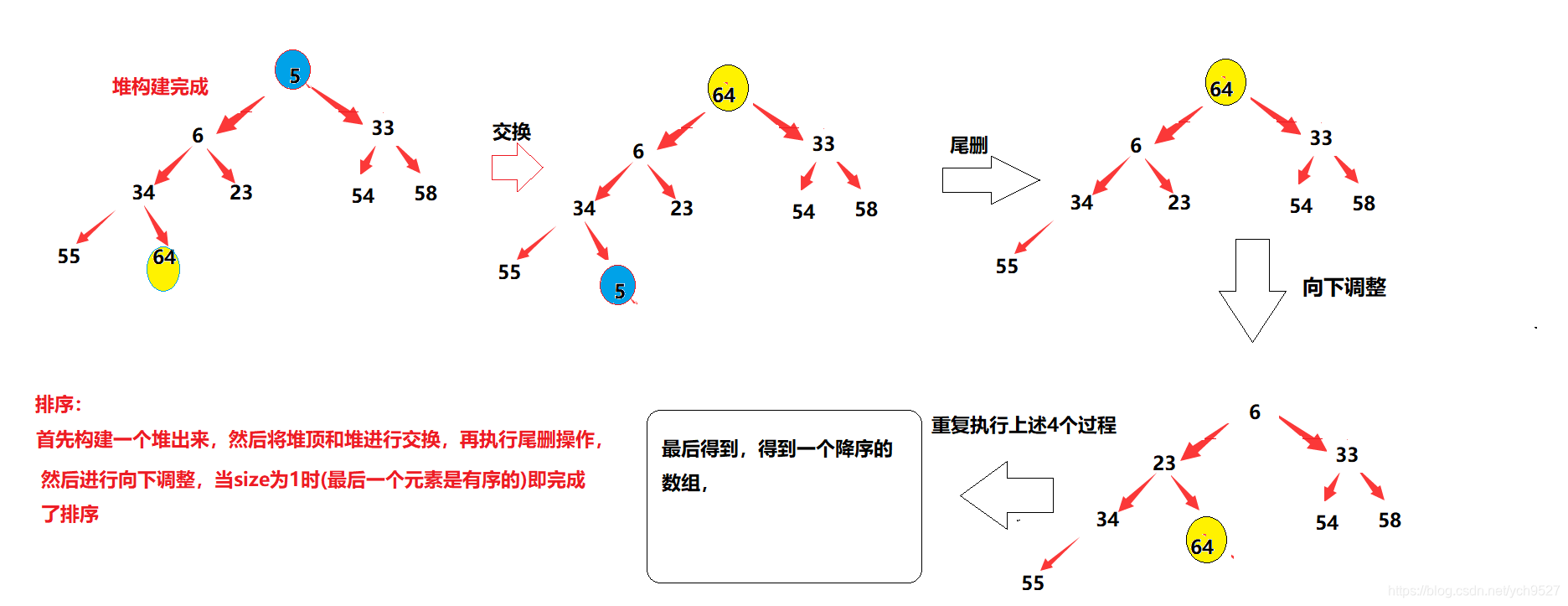
时间复杂度：
建堆的时间复杂度为O(N),有N个元素需要进行交换向下调整时间复杂度为NlogN，
因此实际时间复杂度为NlogN;
实现代码：

void HeapSort(int *arr, int n)//对数组进行排序
{
	int size = n;
	int parent = (size - 2) / 2;
	while (parent>=0)//构建堆
	{
		ShiftDown(arr, size, parent);
		parent--;
	}
	while (size  > 1)
	{
		Swap(arr, 0, size - 1);//交换
		size--;
		ShiftDown(arr, size, 0);
	}
	for (int i = 0; i < n; i++)
	{
		printf("%d ", arr[i]);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

4.堆的元素个数、取堆顶个数以及堆的判空和堆的销毁

这里的实现比较简单，直接利用堆中的size就可以完成，直接上代码

HPDataType HeapTop(Heap *hp)
{
	assert(hp);
	if (hp->size == 0)
		exit(-1);
	return hp->arr[0];
}

HPDataType heapSize(Heap *hp)
{
	assert(hp);
	return hp->size;
}

int HeapEmpty(Heap *hp)
{
	assert(hp);
	if (hp->size == 0)//为空
	{
		printf("堆为空\n");
		return 1;
	}
	else
	{
		printf("非空\n");
		return 0;
	}
}

void HeapDestory(Heap *hp)//堆的销毁
{
	assert(hp);
	hp->size = hp->capacity = 0;
	free(hp->arr);
	hp->arr = NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

5.Top K问题

给N个数，如何寻找其中最小的K个数呢？

我们可以取N的前K个数构建一个大堆，然后从剩余的N-K个数之中取出数来与大堆根进行比较，比大堆根小的就将其替换，并且对大堆根进行向下调整；

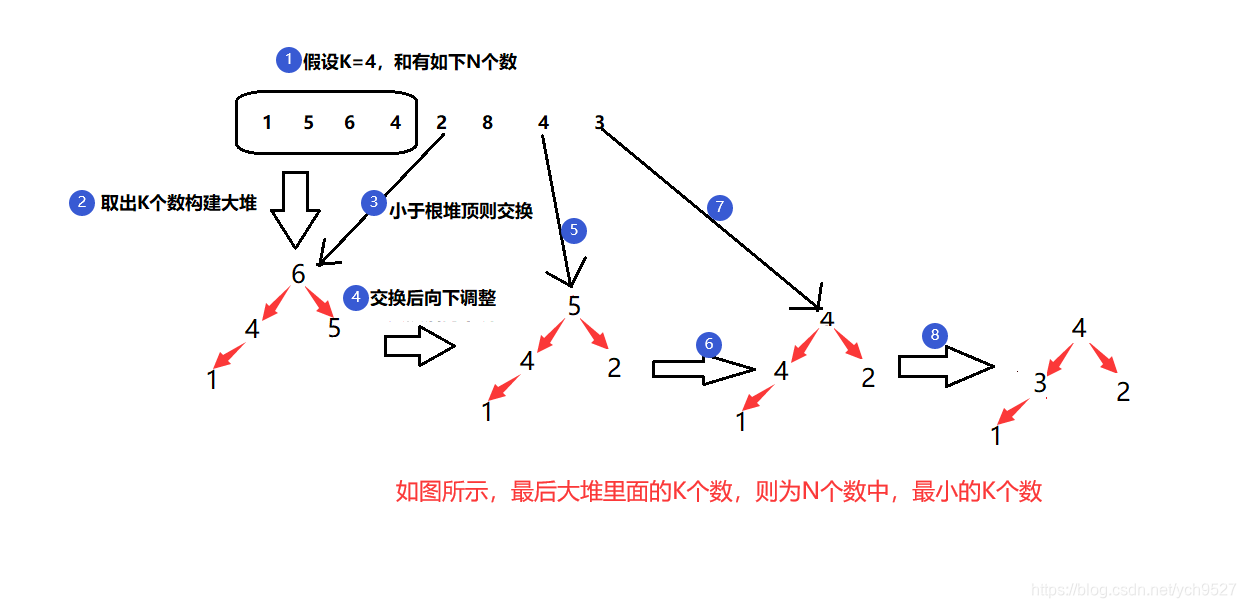
实现代码：

void TopK(HPDataType *arr, int size, int k)
{
	assert(arr);
	Heap hp;
	heapCreate(&hp, arr, k);//建堆


	int n = k;
	while (n<size)
	{
		if (arr[n]<hp.arr[0])//小于根堆顶则交换
		{
			hp.arr[0] = arr[n];
			ShiftDown(hp.arr,k,0);//向下调整
		}
		n++;
	}

	Print(&hp,hp.size);

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21