我家自动化

这个屌丝很懒，什么也没留下！

热门标签

Leetcode Top100题目和答案（Java完整版面试必备）_leetcode答案 java

作者：我家自动化 | 2024-02-20 01:47:57

踩

leetcode答案 java

二刷完剑指Offer后又刷了一遍Leetcode Top 100专栏的题目，听说基本上能涵盖面试的算法题，总体来说收获还是很大的，下面贴出答案，又不懂的可以给我留言，博主会及时解答。
我的github
准备把春招复习的知识都整理到github上，一边是自己做个总结，一边也能供大家参考
——leetcode数据库 19道题
——剑指Offer 66道题

以下摘自leetcode Top100精选题目

文章目录

1.两数之和

题目描述：

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那两个整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，你不能重复利用这个数组中同样的元素。

示例:

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
1
2
3
4

Solution:

class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            if (map.containsKey(nums[i])) {
                return new int[]{map.get(nums[i]), i};
            }
            map.put(target - nums[i], i);
        }
        return null;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

2.两数相加

题目描述：

给出两个非空的链表用来表示两个非负的整数。其中，它们各自的位数是按照逆序的方式存储的，并且它们的每个节点只能存储一位数字。

如果，我们将这两个数相加起来，则会返回一个新的链表来表示它们的和。

您可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例：

输入：(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出：7 -> 0 -> 8
原因：342 + 465 = 807
1
2
3

节点结构：

public class ListNode {
    int val;
    ListNode next;
    ListNode(int x) { val = x; }
}
1
2
3
4
5

Solution:

class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode(0);
        
        int sum = 0; // 结果
        int more = 0; // 进位
        ListNode pre = dummy;
        while (l1 != null || l2 != null || more > 0) {
            sum = (l1 == null ? 0 : l1.val) + (l2 == null ? 0 : l2.val) + more;
            more = sum / 10;
            sum %= 10;
            ListNode node = new ListNode(sum);
            pre.next = node;
            pre = node;
            l1 = l1 == null ? null : l1.next;
            l2 = l2 == null ? null : l2.next;
        }
        return dummy.next;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

3.无重复字符的最长子串

题目描述：

给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。
1
2
3

示例 2:

输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。
1
2
3

示例 3:

输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。
1
2
3
4

Solution:

class Solution {
    public int lengthOfLongestSubstring(String s) {
        if (s == null || s.length() < 1) {
            return 0;
        }
        
        int[] map = new int[256];
        int l = 0;
        int r = 0; // 滑动窗口为[l, r)，其间为不重复的元素
        int res = 0;
        while (l < s.length()) {
            if (r < s.length() && map[s.charAt(r)] == 0) {
                map[s.charAt(r++)]++;
                res = Math.max(res, r - l);
            } else {
                map[s.charAt(l++)]--;
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

4.寻找两个有序数组的中位数

题目描述：

给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。

请你找出这两个有序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。

你可以假设 nums1 和 nums2 不会同时为空。

示例 1:

nums1 = [1, 3]
nums2 = [2]

则中位数是 2.0
1
2
3
4

示例 2:

nums1 = [1, 2]
nums2 = [3, 4]

则中位数是 (2 + 3)/2 = 2.5
1
2
3
4

Solution：

public class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        // 保证nums1不是最长的，时间复杂度可转化为O(log(Min(m, n)))
        if (nums1.length > nums2.length) {
            return findMedianSortedArrays(nums2, nums1);
        }

        int left = 0;
        int right = nums1.length;
        int halfLen = (nums1.length + nums2.length + 1) >> 1;

        while (left <= right) {
            int i = (left + right) >> 1; // nums1[i, nums1.length)为要分割的右半部分
            int j = halfLen - i; // nums2[j, nums2.length)为要分割的右半部分
            if (i < right && nums2[j - 1] > nums1[i]) { // nums1分割点此时需要右移
                left++;
            } else if (i > left && nums1[i - 1] > nums2[j]) { // nums1 分割点此时需要左移
                right--;
            } else {
                int leftMax = (i == 0) ? nums2[j - 1] :
                        (j == 0 ? nums1[i - 1] : Math.max(nums1[i - 1], nums2[j - 1]));
                if (((nums1.length + nums2.length) & 1) == 1) {
                    return leftMax * 1.0;
                }
                int rightMin = (i == nums1.length) ? nums2[j] :
                        (j == nums2.length ? nums1[i] : Math.min(nums1[i], nums2[j]));
                return (leftMax + rightMin) / 2.0;
            }
        }
        return 0.0;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

5.最长回文子串

题目描述：

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
1
2
3

示例 2：

输入: "cbbd"
输出: "bb"
1
2

Solution：

/**
 * 中心扩展法
 */
public class Solution {
    private int left;
    private int len;

    public String longestPalindrome(String s) {
        if (s == null || s.length() < 2) {
            return s;
        }

        for (int i = 0; i < s.length(); i++) {
            find(s, i, i); // 奇数长度
            find(s, i, i + 1); // 偶数长度
        }
        return s.substring(left, left + len);
    }

    private void find(String s, int left, int right) {
        while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
            if (right - left + 1 > len) {
                len = right - left + 1;
                this.left = left;
            }
            right++;
            left--;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

10.正则表达式匹配

题目描述：

给定一个字符串 (s) 和一个字符模式 (p)。实现支持 '.' 和 '*' 的正则表达式匹配。

'.' 匹配任意单个字符。
'*' 匹配零个或多个前面的元素。
1
2

匹配应该覆盖整个字符串 (s) ，而不是部分字符串。

说明:

s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 *。

示例 1:

输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。
1
2
3
4
5

示例 2:

输入:
s = "aa"
p = "a*"
输出: true
解释: '*' 代表可匹配零个或多个前面的元素, 即可以匹配 'a' 。因此, 重复 'a' 一次, 字符串可变为 "aa"。
1
2
3
4
5

示例 3:

输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个('*')任意字符('.')。
1
2
3
4
5

示例 4:

输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 'c' 可以不被重复, 'a' 可以被重复一次。因此可以匹配字符串 "aab"。
1
2
3
4
5

示例 5:

输入:
s = "mississippi"
p = "mis*is*p*."
输出: false
1
2
3
4

Solution：

public class Solution {
    public boolean isMatch(String s, String p) {
        if (s == null || p == null) {
            return false;
        }

        return isMatch(s, p, 0, 0);
    }

    private boolean isMatch(String str, String pattern, int s, int p) {
        // 正则表达式已用尽，如果字符串还未匹配完，则返回false
        if (p == pattern.length()) {
            return str.length() == s;
        }
        // 正则表达式下一位为*，此时考虑两种情况
        if (p + 1 < pattern.length() && pattern.charAt(p + 1) == '*') {
            // 若正则表达式当前位字符与字符串当前位置相匹配，则匹配1位或者0位
            if (s < str.length() && (str.charAt(s) == pattern.charAt(p) || pattern.charAt(p) == '.')) {
                return isMatch(str, pattern, s, p + 2) || isMatch(str, pattern, s + 1, p);
            }
            // 若正则表达式当前位字符与字符串当前位置不匹配，则匹配0位
            return isMatch(str, pattern, s, p + 2);
        }

        // 匹配1位
        if (s < str.length() && (str.charAt(s) == pattern.charAt(p) || pattern.charAt(p) == '.')) {
            return isMatch(str, pattern, s + 1, p + 1);
        }
        return false;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

11.盛最多水的容器

题目描述：

给定 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

**说明：**你不能倾斜容器，且 n 的值至少为 2。

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例:

输入: [1,8,6,2,5,4,8,3,7]
输出: 49
1
2

Solution：

/**
* 利用滑动窗口解决
*/
public class Solution {
    public int maxArea(int[] height) {
        int res = 0;
        int left = 0;
        int right = height.length - 1;
        
        while (left < right) {
            res = Math.max(res, Math.min(height[left], height[right]) * (right - left));
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }
        
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

15.三数之和

题目描述：

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 *a，b，c ，*使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。

**注意：**答案中不可以包含重复的三元组。

例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4]，

满足要求的三元组集合为：
[
  [-1, 0, 1],
  [-1, -1, 2]
]
1
2
3
4
5
6
7

Solution：

/**
 * 采用滑动窗口，时间复杂度为：O(n log(n))
 */
public class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> list = new ArrayList<>();
        if (nums == null || nums.length < 3) {
            return list;
        }

        // 先排序，同时避免求重复解
        Arrays.sort(nums);

        for (int i = 0; i < nums.length - 2 && nums[i] <= 0;) {
            int l = i + 1;
            int r = nums.length - 1;
            while (l < r) {
                int sum = nums[i] + nums[l] + nums[r];
                if (sum == 0) {
                    list.add(Arrays.asList(nums[i], nums[l++], nums[r--]));
                    while (l < r && nums[l] == nums[l - 1]) {
                        l++;
                    }
                    while (r > l && nums[r] == nums[r + 1]) {
                        r--;
                    }
                } else if (sum < 0) {
                    l++;
                } else {
                    r--;
                }
            }
            i++;
            while (i < nums.length - 2 && nums[i] == nums[i - 1]) {
                i++;
            }
        }
        return list;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

17.电话号码的字母组合

题目描述：

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例:

输入："23"
输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
1
2

说明:
尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

Solution：

public class Solution {
    private List<String> res = new ArrayList<>();
    private String[] map = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};

    public List<String> letterCombinations(String digits) {
        if (digits == null || digits.length() < 1) {
            return res;
        }

        dfs(digits, 0, "");
        return res;
    }

    private void dfs(String digits, int index, String str) {
        if (index == digits.length()) {
            res.add(str);
            return;
        }
        
        String dict = map[digits.charAt(index) - '0'];
        for (int i = 0; i < dict.length(); i++) {
            dfs(digits, index + 1, str + dict.charAt(i));
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

19.删除链表的倒数第N个节点

题目描述：

给定一个链表，删除链表的倒数第 n 个节点，并且返回链表的头结点。

示例：

给定一个链表: 1->2->3->4->5, 和 n = 2.

当删除了倒数第二个节点后，链表变为 1->2->3->5.
1
2
3

说明：

给定的 n 保证是有效的。

进阶：

你能尝试使用一趟扫描实现吗？

Solution：

/*
* 双指针
*/
public class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dummy = new ListNode(0);
        dummy.next = head;
        ListNode fast = head;
        ListNode slow = dummy;
        for (int i = 0; i < n; i++) {
            fast = fast.next;
        }
        while (fast != null) {
            fast = fast.next;
            slow = slow.next;
        }
        slow.next = slow.next.next;
        return dummy.next;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

20有效的括号

题目描述：

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。

注意空字符串可被认为是有效字符串。

示例 1:

输入: "()"
输出: true

1
2
3

示例 2:

输入: "()[]{}"
输出: true

1
2
3

示例 3:

输入: "(]"
输出: false

1
2
3

示例 4:

输入: "([)]"
输出: false

1
2
3

示例 5:

输入: "{[]}"
输出: true
1
2

Solution：

public class Solution {
    public static boolean isValid(String s) {
        if (s == null || (s.length() & 1) == 1) {
            return false;
        }

        Stack<Character> stack = new Stack<>();
        for (int i = 0; i < s.length(); i++) {
            if (s.charAt(i) == '[' || s.charAt(i) == '{' || s.charAt(i) == '(') {
                stack.push(s.charAt(i));
            } else if (s.charAt(i) == ']' && (stack.isEmpty() || stack.pop() != '[')) {
                return false;
            } else if (s.charAt(i) == '}' && (stack.isEmpty() || stack.pop() != '{')) {
                return false;
            } else if (s.charAt(i) == ')' && (stack.isEmpty() || stack.pop() != '(')) {
                return false;
            }
        }
        return stack.isEmpty();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

21.合并两个有序链表

题目描述：

将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例：

输入：1->2->4, 1->3->4
输出：1->1->2->3->4->4
1
2

Solution：

public class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode(0);
        ListNode pre = dummy;
        
        while (l1 != null && l2 != null) {
            if (l1.val < l2.val) {
                pre.next = l1;
                l1 = l1.next;
            } else {
                pre.next = l2;
                l2 = l2.next;
            }
            pre = pre.next;
        }
        pre.next = l1 == null ? l2 : l1;
        
        return dummy.next;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

22.生成括号

题目描述：

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

例如，给出 n = 3，生成结果为：

[
  "((()))",
  "(()())",
  "(())()",
  "()(())",
  "()()()"
]
1
2
3
4
5
6
7

Solution：

public class Solution {
    private List<String> list = new ArrayList<>();
    
    public List<String> generateParenthesis(int n) {
        if (n < 1) {
            return list;
        }
        
        generate(n, 0, 0, "");
        return list;
    }
    
    private void generate(int n, int left, int right, String str) {
        if (left == right && left == n) {
            list.add(str);
        }
        if (left < n) {
            generate(n, left + 1, right, str + "(");
        }
        if (left > right) {
            generate(n, left, right + 1, str + ")");
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

23.合并K个排序链表

题目描述：

合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。

示例:

输入:
[
  1->4->5,
  1->3->4,
  2->6
]
输出: 1->1->2->3->4->4->5->6
1
2
3
4
5
6
7

Solution：

public class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if (lists == null || lists.length == 0) {
            return null;
        }

        ListNode dummy = new ListNode(0);
        ListNode pre = dummy;

        // 使用小顶堆，每次取出的都是最小的节点
        Queue<ListNode> minHeap = new PriorityQueue<>(Comparator.comparingInt(node -> node.val));
        for (ListNode list : lists) {
            if (list != null) {
                minHeap.offer(list);
            }
        }

        while (!minHeap.isEmpty()) {
            pre.next = minHeap.poll();
            pre = pre.next;
            if (pre.next != null) {
                minHeap.offer(pre.next);
            }
        }

        return dummy.next;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

31.下一个排列

题目描述：

实现获取下一个排列的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列。

如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

必须原地修改，只允许使用额外常数空间。

以下是一些例子，输入位于左侧列，其相应输出位于右侧列。
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1

Solution：

/**
 * 求下一个全排列，可分为两种情况：
 * 1.例如像 5 4 3 2 1这样的序列，已经是最大的排列，即每个位置上的数非递增，这时只需要翻转整个序列即可
 * 2.例如像 1 3 5 4 2这样的序列，要从后往前找到第一个比后面一位小的元素的位置，即第二个位置的3，然后与其后第一个比它大的元素交换位置，得到 1 4 5 3 2，再将 5 3 2翻转得到 1 4 2 3 5即可
 */

public class Solution {
    public void nextPermutation(int[] nums) {
        if (nums == null || nums.length == 0) {
            return;
        }

        int firstSmall = -1;
        for (int i = nums.length - 2; i >= 0; i--) {
            if (nums[i] < nums[i + 1]) {
                firstSmall = i;
                break;
            }
        }

        if (firstSmall == -1) {
            reverse(nums, 0, nums.length - 1);
            return;
        }

        for (int i = nums.length - 1; i > firstSmall; i--) {
            if (nums[i] > nums[firstSmall]) {
                swap(nums, i, firstSmall);
                reverse(nums, firstSmall + 1, nums.length - 1);
                return;
            }
        }
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

    private void reverse(int[] nums, int start, int end) {
        while (start < end) {
            swap(nums, start++, end--);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

32.最长有效括号

题目描述：

给定一个只包含 '(' 和 ')' 的字符串，找出最长的包含有效括号的子串的长度。

示例 1:

输入: "(()"
输出: 2
解释: 最长有效括号子串为 "()"

1
2
3
4

示例 2:

输入: ")()())"
输出: 4
解释: 最长有效括号子串为 "()()"
1
2
3

Solution：

public class Solution {
    public int longestValidParentheses(String s) {
        if (s == null || s.length() < 2) {
            return 0;
        }

        int res = 0;
        int start = 0;
        Stack<Integer> stack = new Stack<>();
        for (int i = 0; i < s.length(); i++) {
            if (s.charAt(i) == '(') {
                stack.push(i);
            } else {
                if (stack.isEmpty()) {
                    start = i + 1;
                } else {
                    stack.pop();
                    res = stack.isEmpty() ? Math.max(res, i - start + 1) : Math.max(res, i - stack.peek());
                }
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

33.搜索旋转排序数组

题目描述：

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。

你可以假设数组中不存在重复的元素。

你的算法时间复杂度必须是 O(log n) 级别。

示例 1:

输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4

1
2
3

示例 2:

输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1
1
2

Solution：

public class Solution {
    public int search(int[] nums, int target) {
        if (nums == null 
            || nums.length < 1 
            || (target < nums[0] && target > nums[nums.length - 1])) {
            return -1;
        }
        
        int low = 0;
        int high = nums.length - 1;
        while (low <= high) {
            int mid = (low + high) >> 1;
            if (nums[mid] == target) {
                return mid;
            }
            
            if (nums[mid] >= nums[low]) {// 左边有序
                if (nums[mid] > target && nums[low] <= target) {// 在有序边
                    high = mid - 1;
                } else{// 在无序边
                    low = mid + 1;
                }
            } else {// 右边有序
                if (nums[mid] < target && nums[high] >= target) {// 在有序边
                    low = mid + 1;
                } else {// 在无序边
                    high = mid - 1;
                }
            }
        }
        
        return -1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

34.在排序数组中查找元素的第一个和最后一个位置

题目描述：

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

你的算法时间复杂度必须是 O(log n) 级别。

如果数组中不存在目标值，返回 [-1, -1]。

示例 1:

输入: nums = [5,7,7,8,8,10], target = 8
输出: [3,4]

1
2
3

示例 2:

输入: nums = [5,7,7,8,8,10], target = 6
输出: [-1,-1]
1
2

Solution：

public class Solution {
    public int[] searchRange(int[] nums, int target) {
        if (nums == null || nums.length < 1) {
            return new int[]{-1, -1};
        }
        
        int low = 0;
        int high = nums.length - 1;
        while (low <= high) {
            int mid = (low + high) >> 1;
            if (nums[mid] < target) {
                low = mid + 1;
            } else if (nums[mid] > target) {
                high = mid - 1;
            } else {
                int left = mid;
                int right = mid;
                while (left >= low && nums[left] == target) {
                    left--;
                }
                while (right <= high && nums[right] == target) {
                    right++;
                }
                return new int[]{left + 1, right -1};
            }
        }
        
        return new int[]{-1, -1};
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

39.组合总和

题目描述：

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

所有数字（包括 target）都是正整数。
解集不能包含重复的组合。

示例 1:

输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
  [7],
  [2,2,3]
]

1
2
3
4
5
6
7

示例 2:

输入: candidates = [2,3,5], target = 8,
所求解集为:
[
  [2,2,2,2],
  [2,3,3],
  [3,5]
]
1
2
3
4
5
6
7

Solution：

public class Solution {
    private List<List<Integer>> res = new ArrayList<>();;

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        if (candidates == null || candidates.length == 0) {
            return res;
        }
        dfs(candidates, 0, target, new ArrayList<>());
        return res;
    }

    private void dfs(int[] candidates, int start, int target, List<Integer> list) {
        if (target == 0) {
            res.add(new ArrayList<>(list));
            return;
        }

        for (int i = start; i < candidates.length; i++) {
            if (target >= candidates[i]) {
                list.add(candidates[i]);
                dfs(candidates, i, target - candidates[i], list);
                list.remove(list.size() - 1);
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

42.接雨水

题目描述：

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6
1
2

Solution：

public class Solution {
    public int trap(int[] height) {
        if (height == null || height.length < 3) {
            return 0;
        }
        
        int low = 0;
        int high = height.length - 1;
        int res = 0;
        int lowMax = 0;
        int highMax = 0;
        while (low < high) {
            if (height[low] < height[high]) {
                lowMax = Math.max(lowMax, height[low]);
                res += lowMax - height[low];
                low++;
            } else {
                highMax = Math.max(highMax, height[high]);
                res += highMax - height[high];
                high--;
            }
        }
        
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

46.全排列

题目描述：

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]
1
2
3
4
5
6
7
8
9
10

Solution：

public class Solution {
    private List<List<Integer>> res = new ArrayList<>();
    private boolean[] visited;

    public List<List<Integer>> permute(int[] nums) {
        if (nums == null) {
            return res;
        }
        
        visited = new boolean[nums.length];
        permute(0, nums, new ArrayList());
        return res;
    }
    
    private void permute(int index, int[] nums, List<Integer> list) {
        if (index == nums.length) {
            res.add(new ArrayList(list));
            return;
        }
        
        for (int i = 0; i < nums.length; i++) {
            if (!visited[i]) {
                list.add(nums[i]);
                visited[i] = true;
                permute(index + 1, nums, list);
                list.remove(list.size() - 1);
                visited[i] = false;
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

48.旋转图像

题目描述：

给定一个 n × n 的二维矩阵表示一个图像。

将图像顺时针旋转 90 度。

说明：

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例 1:

给定 matrix = 
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],

原地旋转输入矩阵，使其变为:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

1
2
3
4
5
6
7
8
9
10
11
12
13
14

示例 2:

给定 matrix =
[
  [ 5, 1, 9,11],
  [ 2, 4, 8,10],
  [13, 3, 6, 7],
  [15,14,12,16]
], 

原地旋转输入矩阵，使其变为:
[
  [15,13, 2, 5],
  [14, 3, 4, 1],
  [12, 6, 8, 9],
  [16, 7,10,11]
]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Solution：

/**
 * 以第一个数据为例分析：
 * 1 2 3
 * 4 5 6
 * 7 8 9
 * 先做左右对称翻转，得到：
 * 3 2 1
 * 6 5 4
 * 9 8 7
 * 再以副对角线为轴做翻转，得到：
 * 7 4 1
 * 8 5 2
 * 9 6 3
 * 此时即为要求的结果
 * 故——要先做左右对称翻转，再做一次副对角线翻转即可
 */
public class Solution {
    public void rotate(int[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return;
        }
        
        int n = matrix.length;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < (n >> 1); j++) {
                swap(matrix, i, j, i, n - j - 1);
            }
        }
        
        for (int i = 0; i < n; i++) {
            for (int j = 0; j + i + 1 < n; j++) {
                swap(matrix, i, j, n - 1 - j, n - 1 - i);
            }
        }
    }
    
    private void swap(int[][] matrix, int i, int j, int p, int q) {
        int temp = matrix[i][j];
        matrix[i][j] = matrix[p][q];
        matrix[p][q] = temp;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

49.字母异位词分组

题目描述：

给定一个字符串数组，将字母异位词组合在一起。字母异位词指字母相同，但排列不同的字符串。

示例:

输入: ["eat", "tea", "tan", "ate", "nat", "bat"],
输出:
[
  ["ate","eat","tea"],
  ["nat","tan"],
  ["bat"]
]

1
2
3
4
5
6
7
8

说明：

所有输入均为小写字母。
不考虑答案输出的顺序。

Solution：

public class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        List<List<String>> res = new ArrayList<>();
        if (strs == null || strs.length == 0) {
            return res;
        }

        Map<String, List<String>> map = new HashMap<>();
        for (String str : strs) {
            int[] counts = new int[26];
            for (int i = 0; i < str.length(); i++) {
                counts[str.charAt(i) - 'a']++;
            }

            StringBuilder sb = new StringBuilder();
            for (int count : counts) {
                sb.append(' ').append(count);
            }
            String key = sb.toString();
            if (!map.containsKey(key)) {
                map.put(key, new ArrayList<>());
            }
            map.get(key).add(str);
        }
        return new ArrayList<>(map.values());
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

53.最大子序和

题目描述：

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
1
2
3

Solution：

public class Solution {
    public int maxSubArray(int[] nums) {
        if (nums == null || nums.length == 0) {
            return 0;
        }
        
        int res = nums[0];
        int max = 0;
        for (int num : nums) {
            max = Math.max(max + num, num);
            res = Math.max(res, max);
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

55.跳跃游戏

题目描述：

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个位置。

示例 1:

输入: [2,3,1,1,4]
输出: true
解释: 从位置 0 到 1 跳 1 步, 然后跳 3 步到达最后一个位置。

1
2
3
4

示例 2:

输入: [3,2,1,0,4]
输出: false
解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置。
1
2
3

Solution：

/*
* 从后往前跳
*/
public class Solution {
    public boolean canJump(int[] nums) {
        int last = nums.length - 1;
        for (int i = nums.length - 1; i >= 0; i--) {
            if (nums[i] + i >= last) {
                last = i;
            }
        }
        return last == 0;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

56.合并区间

题目描述：

给出一个区间的集合，请合并所有重叠的区间。

示例 1:

输入: [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

1
2
3
4

示例 2:

输入: [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
1
2
3

Solution：

public class Solution {
    public List<Interval> merge(List<Interval> intervals) {
        if (intervals == null || intervals.size() < 2) {
            return intervals;
        }

        List<Interval> list = new ArrayList<>();
        intervals.sort(Comparator.comparingInt(interval -> interval.start));

        Interval pre = null;
        for (Interval interval : intervals) {
            if (pre == null || pre.end < interval.start) {
                list.add(interval);
                pre = interval;
            } else {
                pre.end = Math.max(pre.end, interval.end);
            }
        }
        return list;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

62.不同路径

题目描述：

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明： m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

1
2
3
4
5
6
7
8

示例 2:

输入: m = 7, n = 3
输出: 28
1
2

Solution：

public class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (i == 0 || j == 0) {
                    dp[i][j] = 1;
                } else {
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                }
            }
        }
        
        return dp[m - 1][n - 1];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

64.最小路径和

题目描述：

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

**说明：**每次只能向下或者向右移动一步。

示例:

输入:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。
1
2
3
4
5
6
7
8

Solution：

public class Solution {
    public int minPathSum(int[][] grid) {
        if (grid == null || grid.length == 0 || grid[0].length == 0) {
            return 0;
        }
        
        int m = grid.length;
        int n = grid[0].length;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (i == 0 && j == 0) {
                    continue;
                }
                if (i == 0) {
                    grid[i][j] += grid[i][j - 1];
                } else if (j == 0) {
                    grid[i][j] += grid[i - 1][j];
                } else {
                    grid[i][j] += Math.min(grid[i - 1][j], grid[i][j - 1]);
                }
            }
        }
        return grid[m - 1][n - 1];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

70.爬楼梯

题目描述：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

**注意：**给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

1
2
3
4
5
6

示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶
1
2
3
4
5
6

Solution：

public class Solution {
    public int climbStairs(int n) {
        int a = 1;
        int b = 1;
        for (int i = 2; i <= n; i++) {
            int temp = b;
            b += a;
            a = temp;
        }
        return b;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

72.编辑距离

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1:

输入: word1 = "horse", word2 = "ros"
输出: 3
解释: 
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

1
2
3
4
5
6
7

示例 2:

输入: word1 = "intention", word2 = "execution"
输出: 5
解释: 
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
1
2
3
4
5
6
7
8

Solution：

public class Solution {
    public int minDistance(String word1, String word2) {
        if (word1 == null || word2 == null) {
            return 0;
        }
        
        int[][] dp = new int[word1.length() + 1][word2.length() + 1];
        for (int i = 1; i <= word1.length(); i++) {
            dp[i][0] = i;
        }
        for (int i = 1; i <= word2.length(); i++) {
            dp[0][i] = i;
        }
        for (int i = 0; i < word1.length(); i++) {
            for (int j = 0; j < word2.length(); j++) {
                if (word1.charAt(i) == word2.charAt(j)) {
                    dp[i + 1][j + 1] = dp[i][j];
                } else {
                    dp[i + 1][j + 1] = Math.min(Math.min(dp[i][j], dp[i + 1][j]), dp[i][j + 1]) + 1;
                }
            }
        }
        
        return dp[word1.length()][word2.length()];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

75.颜色分类

题目描述：

给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

注意:
不能使用代码库中的排序函数来解决这道题。

示例:

输入: [2,0,2,1,1,0]
输出: [0,0,1,1,2,2]
1
2

Solution：

class Solution {
    // 解法一：桶排序
    public void sortColors(int[] nums) {
        if (nums == null) {
            return;
        }
        int[] count = new int[3]; // 统计1、2、3出现的次数
        for (int num : nums) {
            count[num]++;
        }
        int index = 0;
        for (int i = 0; i < count[0]; i++) {
            nums[index++] = 0;
        }
        for (int i = 0; i < count[1]; i++) {
            nums[index++] = 1;
        }
        for (int i = 0; i < count[2]; i++) {
            nums[index++] = 2;
        }
    }

    // 解法二：三路快排
    public void sortColors(int[] nums) {
        if (nums == null) {
            return;
        }
        int zero = -1;// 保证[0, zero]区间内为0
        int two = nums.length;// 保证[two, nums.length - 1]区间内为2
        for (int i = 0; i < two; ) {
            if (nums[i] == 0) {
                nums[i++] = nums[++zero];
                nums[zero] = 0;
            } else if (nums[i] == 2) {
                nums[i] = nums[--two];
                nums[two] = 2;
            } else {
                i++;
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

76.最小覆盖子串

给定一个字符串 S 和一个字符串 T，请在 S 中找出包含 T 所有字母的最小子串。

示例：

输入: S = "ADOBECODEBANC", T = "ABC"
输出: "BANC"

1
2
3

说明：

如果 S 中不存这样的子串，则返回空字符串 ""。
如果 S 中存在这样的子串，我们保证它是唯一的答案。

Solution：

public class Solution {
    public String minWindow(String s, String t) {
        if (s == null || t == null || s.length() < t.length()) {
            return "";
        }

        String res = "";
        int[] sFlag = new int[256];
        int[] tFlag = new int[256];
        for (int i = 0; i < t.length(); i++) {
            tFlag[t.charAt(i)]++;
        }
        int count = t.length();
        int l = 0;
        int r = 0;
        while (l <= s.length() - t.length()) {
            if (count > 0 && r < s.length()) {
                if (sFlag[s.charAt(r)]++ < tFlag[s.charAt(r++)]) {
                    count--;
                }
            } else {
                if (count == 0 && (res.length() == 0 || r - l < res.length())) {
                    res = s.substring(l, r);
                }
                if (sFlag[s.charAt(l)]-- <= tFlag[s.charAt(l++)]) {
                    count++;
                }
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

78.子集

题目描述：

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

**说明：**解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]
1
2
3
4
5
6
7
8
9
10
11
12

Solution：

public class Solution {
    private List<List<Integer>> res = new ArrayList<>();
    
    public List<List<Integer>> subsets(int[] nums) {
        if (nums == null || nums.length == 0) {
            return res;
        }
        
        dfs(nums, 0, new ArrayList<>());
        return res;
    }
    
    private void dfs(int[] nums, int index, List<Integer> list) {
        if (index == nums.length) {
            res.add(new ArrayList<>(list));
            return;
        }
        
        dfs(nums, index + 1, list);
        list.add(nums[index]);
        dfs(nums, index + 1, list);
        list.remove(list.size() - 1);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

79.单词搜索

题目描述：

给定一个二维网格和一个单词，找出该单词是否存在于网格中。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例:

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

给定 word = "ABCCED", 返回 true.
给定 word = "SEE", 返回 true.
给定 word = "ABCB", 返回 false.
1
2
3
4
5
6
7
8
9
10

Solution：

public class Solution {
    private boolean[][] visited;
    private int index = 0;

    public boolean exist(char[][] board, String word) {
        if (board == null || board.length == 0 || board[0].length == 0 || word == null) {
            return false;
        }

        visited = new boolean[board.length][board[0].length];
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                if (exit(board, word, i, j)) {
                    return true;
                }
            }
        }
        return false;
    }

    private boolean exit(char[][] board, String word, int row, int col) {
        if (index == word.length()) {
            return true;
        }

        boolean flag = false;
        if (col >= 0 && col < board[0].length
                && row >= 0 && row < board.length
                && !visited[row][col] && board[row][col] == word.charAt(index)) {
            visited[row][col] = true;
            index++;
            flag = exit(board, word, row + 1, col)
                    || exit(board, word, row - 1, col)
                    || exit(board, word, row, col + 1)
                    || exit(board, word, row, col - 1);
            if (!flag) {
                index--;
                visited[row][col] = false;
            }
        }
        return flag;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

84.柱状图中最大的矩形

题目描述：

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

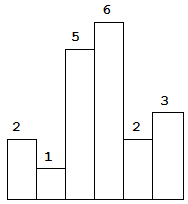
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

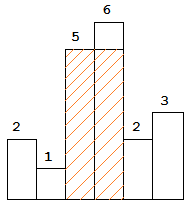
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

1
2
3

Solution：

/**
 * 单调栈
 */
public class Solution {
    public int largestRectangleArea(int[] heights) {
        if (heights == null || heights.length == 0) {
            return 0;
        }

        Stack<Integer> stack = new Stack<>();
        int res = 0;
        for (int i = 0; i <= heights.length; i++) {
            int currentHeight = i == heights.length ? -1 : heights[i];
            while (!stack.isEmpty() && currentHeight <= heights[stack.peek()]) {
                int stackHeight = heights[stack.pop()];
                res = Math.max(res, stackHeight * (stack.isEmpty() ? i : i - stack.peek() - 1));
            }
            stack.push(i);
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

85.最大矩形

题目描述：

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例:

输入:
[
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]
输出: 6
1
2
3
4
5
6
7
8

Solution：

public class Solution {
    public int maximalRectangle(char[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return 0;
        }

        int res = 0;
        int[] height = new int[matrix[0].length];

        for (int i = 0; i < matrix.length; i++) {
            Stack<Integer> stack = new Stack<>();
            for (int j = 0; j <= height.length; j++) {
                if (j < height.length) {
                    height[j] = (matrix[i][j] == '1') ? 1 + height[j] : 0;
                }
                int curHeight = j == height.length ? -1 : height[j];
                while (!stack.isEmpty() && curHeight <= height[stack.peek()]) {
                    int stackHeight = height[stack.pop()];
                    int width = stack.isEmpty() ? j : j - stack.peek() - 1;
                    res = Math.max(res, width * stackHeight);
                }
                stack.push(j);
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

94.二叉树的中序遍历

题目描述：

给定一个二叉树，返回它的中序遍历。

示例:

输入: [1,null,2,3]
   1
    \
     2
    /
   3

输出: [1,3,2]
1
2
3
4
5
6
7
8

Solution：

public class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode node = root;
        while (!stack.isEmpty() || node != null) {
            while (node != null) {
                stack.push(node);
                node = node.left;
            }
            node = stack.pop();
            res.add(node.val);
            node = node.right;
        }
        
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

96.不同的二叉搜索树

题目描述：

给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？

示例:

输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3
1
2
3
4
5
6
7
8
9
10

Solution：

public class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 0; j < i; j++) {
                dp[i] += dp[j] * dp[i - j - 1];
            }
        }
        return dp[n];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13

98.验证二叉搜索树

题目描述：

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1:

输入:
    2
   / \
  1   3
输出: true

1
2
3
4
5
6

示例 2:

输入:
    5
   / \
  1   4
     / \
    3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
     根节点的值为 5 ，但是其右子节点值为 4 。
1
2
3
4
5
6
7
8
9

Solution：

public class Solution {
    public boolean isValidBST(TreeNode root) {
        TreeNode pre = null;
        Stack<TreeNode> stack = new Stack<>();
        TreeNode node = root;
        
        while (!stack.isEmpty() || node != null) {
            while (node != null) {
                stack.push(node);
                node = node.left;
            }
            node = stack.pop();
            if (pre != null && pre.val >= node.val) {
                return false;
            }
            pre = node;
            node = node.right;
        }
        return true;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

101.对称二叉树

题目描述：

给定一个二叉树，检查它是否是镜像对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

Solution：

public class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return true;
        }
        return isSymmetric(root.left, root.right);
    }
    
    private boolean isSymmetric(TreeNode left, TreeNode right) {
        if (left == null && right == null) {
            return true;
        }
        if (left == null || right == null) {
            return false;
        }
        return left.val == right.val && isSymmetric(left.left, right.right) && isSymmetric(left.right, right.left);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

102.二叉树的层序遍历

题目描述：

给定一个二叉树，返回其按层次遍历的节点值。（即逐层地，从左到右访问所有节点）。

例如:
给定二叉树: [3,9,20,null,null,15,7],

返回其层次遍历结果：

[
  [3],
  [9,20],
  [15,7]
]
1
2
3
4
5

Solution：

public class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) {
            return res;
        }
        
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            List<Integer> list = new ArrayList<>();
            while (size-- > 0) {
                TreeNode node = queue.poll();
                list.add(node.val);
                if (node.left != null) {
                    queue.offer(node.left);
                }
                if (node.right != null) {
                    queue.offer(node.right);
                }
            }
            res.add(list);
        }
        
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

104.二叉树的最大深度

题目描述：

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3 。

Solution：

public class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
    }
}
1
2
3
4
5
6
7
8

105.从前序遍历和中序遍历序列构造二叉树

题目描述：

根据一棵树的前序遍历与中序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]

1
2
3

返回如下的二叉树：

Solution：

public class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder == null || inorder == null || preorder.length != inorder.length || preorder.length == 0) {
            return null;
        }
        return build(preorder, inorder, 0, preorder.length - 1, 0, inorder.length - 1);
    }

    private TreeNode build(int[] preorder, int[] inorder, int ps, int pe, int is, int ie) {
        if (ps > pe || is > ie) {
            return null;
        }

        TreeNode node = new TreeNode(preorder[ps]);
        for (int i = is; i <= ie; i++) {
            if (inorder[i] == preorder[ps]) {
                node.left = build(preorder, inorder, ps + 1, i - is + ps, is, i - 1);
                node.right = build(preorder, inorder, i - is + ps + 1, pe, i + 1, ie);
                return node;
            }
        }
        return node;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

114.二叉树展开为链表

题目描述：

给定一个二叉树，原地将它展开为链表。

例如，给定二叉树

将其展开为：

Solution：

public class Solution {
    private TreeNode last = new TreeNode(0);

    public void flatten(TreeNode root) {
        if (root == null) {
            return;
        }
        last.right = root;
        last.left = null;
        last = last.right;
        TreeNode temp = root.right;
        
        flatten(root.left);
        flatten(temp);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

121.买卖股票的最佳时机

题目描述：

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

示例 1:

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

1
2
3
4
5

示例 2:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
1
2
3

Solution：

public class Solution {
    public int maxProfit(int[] prices) {
        if (prices == null || prices.length == 0) {
            return 0;
        }
        
        int res = 0;
        int curMin = prices[0];
        for (int price : prices) {
            res = Math.max(res, price - curMin);
            curMin = Math.min(price, curMin);
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

124.二叉树中的最大路径和

题目描述：

给定一个非空二叉树，返回其最大路径和。

本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。

示例 1:

输入: [1,2,3]

       1
      / \
     2   3

输出: 6

1
2
3
4
5
6
7
8

示例 2:

输入: [-10,9,20,null,null,15,7]

   -10
   / \
  9  20
    /  \
   15   7

输出: 42
1
2
3
4
5
6
7
8
9

Solution：

public class Solution {
    private int res = Integer.MIN_VALUE;
    
    public int maxPathSum(TreeNode root) {
        helper(root);
        return res;
    }
    
    private int helper(TreeNode root) {
        if (root == null) {
            return 0;
        }
        
        int left = Math.max(0, helper(root.left));
        int right = Math.max(0, helper(root.right));
        res = Math.max(res, left + right + root.val);
        return root.val + Math.max(left, right);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

128.最长连续序列

题目描述：

给定一个未排序的整数数组，找出最长连续序列的长度。

要求算法的时间复杂度为 O(n)。

示例:

输入: [100, 4, 200, 1, 3, 2]
输出: 4
解释: 最长连续序列是 [1, 2, 3, 4]。它的长度为 4。
1
2
3

Solution：

public class Solution {
    public int longestConsecutive(int[] nums) {
        if (nums == null || nums.length == 0) {
            return 0;
        }

        // 以key开始，连续序列长度为value
        Map<Integer, Integer> map = new HashMap<>();
        int res = 0;
        for (int num : nums) {
            if (map.containsKey(num)) {
                continue;
            }
            map.put(num, 1 + map.getOrDefault(num + 1, 0));
            // 更新其左边相邻元素的连续序列长度
            while (map.containsKey(num - 1)) {
                map.put(num - 1, map.get(num--) + 1);
            }
        }
        for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
            res = Math.max(res, entry.getValue());
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

136.只出现一次的数字

题目描述：

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。你可以不使用额外空间来实现吗？

示例 1:

输入: [2,2,1]
输出: 1

1
2
3

示例 2:

输入: [4,1,2,1,2]
输出: 4

1
2
3

Solution：

public class Solution {
    public int singleNumber(int[] nums) {
        int res = 0;
        for (int num : nums) {
            res ^= num;
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9

139.单词拆分

题目描述：

给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

说明：

拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。

示例 1：

输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。

1
2
3
4

示例 2：

输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
     注意你可以重复使用字典中的单词。

1
2
3
4
5

示例 3：

输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false
1
2

Solution：

public class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        if (s == null || "".equals(s)) {
            return true;
        }
        
        boolean[] dp = new boolean[s.length() + 1];
        dp[0] = true;
        
        for (int i = 1; i <= s.length(); i++) {
            for (int j = 0; j < i; j++) {
                String sub = s.substring(j, i);
                if (dp[j] && wordDict.contains(sub)) {
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp[s.length()];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

141.环形链表

题目描述：

给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

1
2
3
4

示例 2：

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

1
2
3
4

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

1
2
3
4

Solution：

public class Solution {
    public boolean hasCycle(ListNode head) {
        if (head == null) {
            return false;
        }
        
        ListNode fast = head;
        ListNode slow = head;
        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
            if (fast == slow) {
                break;
            }
        }
        return fast != null && fast.next != null;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

142.环形链表Ⅱ

题目描述：

给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。

**说明：**不允许修改给定的链表。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：tail connects to node index 1
解释：链表中有一个环，其尾部连接到第二个节点。

1
2
3
4

示例 2：

输入：head = [1,2], pos = 0
输出：tail connects to node index 0
解释：链表中有一个环，其尾部连接到第一个节点。

1
2
3
4

示例 3：

输入：head = [1], pos = -1
输出：no cycle
解释：链表中没有环。

1
2
3
4

Solution：

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        
        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
            if (fast == slow) {
                break;
            }
        }
        if (fast == null || fast.next == null) {
            return null;
        }
        
        slow = head;
        while (slow != fast) {
            slow = slow.next;
            fast = fast.next;
        }
        return fast;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

146.LRU缓存机制

题目描述：

运用你所掌握的数据结构，设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作：获取数据 get 和写入数据 put 。

获取数据 get(key) - 如果密钥 (key) 存在于缓存中，则获取密钥的值（总是正数），否则返回 -1。
写入数据 put(key, value) - 如果密钥不存在，则写入其数据值。当缓存容量达到上限时，它应该在写入新数据之前删除最近最少使用的数据值，从而为新的数据值留出空间。

进阶:

你是否可以在 O(1) 时间复杂度内完成这两种操作？

示例:

LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );

cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // 返回  1
cache.put(3, 3);    // 该操作会使得密钥 2 作废
cache.get(2);       // 返回 -1 (未找到)
cache.put(4, 4);    // 该操作会使得密钥 1 作废
cache.get(1);       // 返回 -1 (未找到)
cache.get(3);       // 返回  3
cache.get(4);       // 返回  4
1
2
3
4
5
6
7
8
9
10
11

Solution：

public class LRUCache {
    private LinkedHashMap<Integer, Integer> map;
    private int capacity;

    public LRUCache(int capacity) {
        map = new LinkedHashMap<Integer, Integer>(16, 0.75f, true) {
            @Override
            protected boolean removeEldestEntry(Map.Entry eldest) {
                return size() > LRUCache.this.capacity;
            }
        };
        this.capacity = capacity;
    }

    public int get(int key) {
        return map.getOrDefault(key, -1);
    }

    public void put(int key, int value) {
        map.put(key, value);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

148.排序链表

题目描述：

在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序。

示例 1:

输入: 4->2->1->3
输出: 1->2->3->4

1
2
3

示例 2:

输入: -1->5->3->4->0
输出: -1->0->3->4->5
1
2

Solution：

public class Solution {
    public ListNode sortList(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        ListNode mid = getMid(head);
        ListNode second = mid.next;
        mid.next = null;
        return merge(sortList(head), sortList(second));
    }
    
    private ListNode merge(ListNode first, ListNode second) {
        ListNode dummy = new ListNode(0);
        ListNode pre = dummy;
        while (first != null && second != null) {
            if (first.val > second.val) {
                pre.next = second;
                second = second.next;
            } else {
                pre.next = first;
                first = first.next;
            }
            pre = pre.next;
        }
        pre.next = first == null ? second : first;
        return dummy.next;
    }
    
    private ListNode getMid(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        while (fast.next != null && fast.next.next != null) {
            fast = fast.next.next;
            slow = slow.next;
        }
        return slow;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

152.乘机最大子序列

题目描述：

给定一个整数数组 nums ，找出一个序列中乘积最大的连续子序列（该序列至少包含一个数）。

示例 1:

输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。

1
2
3
4

示例 2:

输入: [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。

1
2
3
4

Solution：

public class Solution {
    public int maxProduct(int[] nums) {
        int res = nums[0];
        int max = 1;
        int min = 1;
        for (int num : nums) {
            if (num < 0) {
                int temp = min;
                min = max;
                max = temp;
            }
            max = Math.max(max * num, num);
            min = Math.min(min * num, num);
            res = Math.max(max, res);
        }
        
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

155.最小栈

题目描述：

设计一个支持 push，pop，top 操作，并能在常数时间内检索到最小元素的栈。

push(x) – 将元素 x 推入栈中。
pop() – 删除栈顶的元素。
top() – 获取栈顶元素。
getMin() – 检索栈中的最小元素。

示例:

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.
1
2
3
4
5
6
7
8

Solution：

public class MinStack {
    private Stack<Integer> stack = new Stack<>();
    private Stack<Integer> minStack = new Stack<>();
        
    /** initialize your data structure here. */
    public MinStack() {
    }
    
    public void push(int x) {
        stack.push(x);
        if (minStack.isEmpty() || minStack.peek() > x) {
            minStack.push(x);
        } else {
            minStack.push(minStack.peek());
        }
    }
    
    public void pop() {
        minStack.pop();
        stack.pop();
    }
    
    public int top() {
        return stack.peek();
    }
    
    public int getMin() {
        return minStack.peek();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

160.相交链表

题目描述：

编写一个程序，找到两个单链表相交的起始节点。

如下面的两个链表**：**

在节点 c1 开始相交。

示例 1：

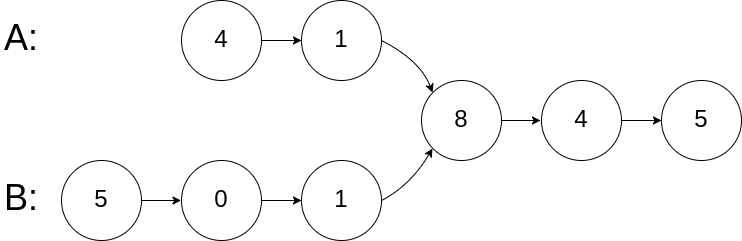
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出：Reference of the node with value = 8
输入解释：相交节点的值为 8 （注意，如果两个列表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

1
2
3
4

示例 2：

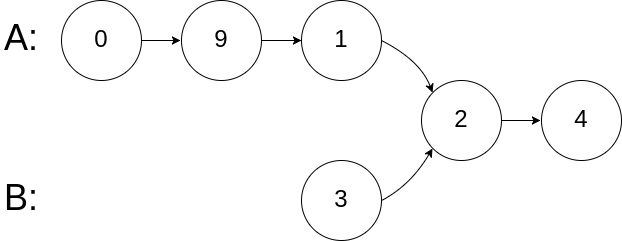
输入：intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Reference of the node with value = 2
输入解释：相交节点的值为 2 （注意，如果两个列表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [0,9,1,2,4]，链表 B 为 [3,2,4]。在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

1
2
3
4

示例 3：

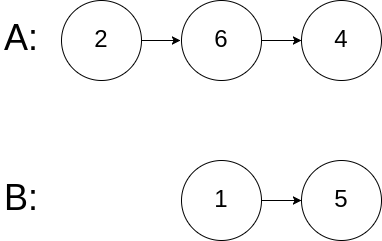
输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
输入解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
解释：这两个链表不相交，因此返回 null。

1
2
3
4
5

注意：

如果两个链表没有交点，返回 null.
在返回结果后，两个链表仍须保持原有的结构。
可假定整个链表结构中没有循环。
程序尽量满足 O(n) 时间复杂度，且仅用 O(1) 内存。

Solution：

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if (headA == null || headB == null) {
            return null;
        }
        
        ListNode a = headA;
        ListNode b = headB;
        while (a != b) {
            a = a == null ? headB : a.next;
            b = b == null ? headA : b.next;
        }
        return a;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

169.求众数

题目描述：

给定一个大小为 n 的数组，找到其中的众数。众数是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在众数。

示例 1:

输入: [3,2,3]
输出: 3

1
2
3

示例 2:

输入: [2,2,1,1,1,2,2]
输出: 2

1
2
3

Solution：

/**
* 摩尔投票法
*/
public class Solution {
    public int majorityElement(int[] nums) {
        int count = 1;
        int res = nums[0];
        for (int num : nums) {
            if (num == res) {
                count++;
            } else {
                if (count == 1) {
                    res = num;
                } else {
                    count--;
                }
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

198.打家劫舍

题目描述：

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你**在不触动警报装置的情况下，**能够偷窃到的最高金额。

示例 1:

输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。

1
2
3
4
5

示例 2:

输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
     偷窃到的最高金额 = 2 + 9 + 1 = 12 。
1
2
3
4

Solution：

public class Solution {
    public int rob(int[] nums) {
        if (nums == null || nums.length == 0) {
            return 0;
        }
        if (nums.length == 1) {
            return nums[0];
        }
        
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        dp[1] = Math.max(nums[0], nums[1]);
        for (int i = 2; i < nums.length; i++) {
            dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);
        }
        return dp[nums.length - 1];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

200.岛屿的个数

题目描述：

给定一个由 '1'（陆地）和 '0'（水）组成的的二维网格，计算岛屿的数量。一个岛被水包围，并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。

示例 1:

示例 2:

Solution：

public class Solution {
    private boolean[][] visited;
    
    public int numIslands(char[][] grid) {
        if (grid == null || grid.length == 0 || grid[0].length == 0) {
            return 0;
        }
        
        int res = 0;
        visited = new boolean[grid.length][grid[0].length];
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == '1' && !visited[i][j]) {
                    res++;
                    dfs(grid, i, j);
                }
            }
        }
        
        return res;
    }
    
    private void dfs (char[][] grid, int row, int col) {
        if (row < 0 || row >= grid.length || col < 0 || col >= grid[0].length || grid[row][col] == '0' || visited[row][col]) {
            return;
        }
        
        visited[row][col] = true;
        dfs(grid, row + 1, col);
        dfs(grid, row - 1, col);
        dfs(grid, row, col + 1);
        dfs(grid, row, col - 1);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

206.反转链表

题目描述：

反转一个单链表。

示例:

输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL
1
2

Solution：

public class Solution {
    // 解法一
    public ListNode reverseList(ListNode head) {
        ListNode dummy = new ListNode(0);
        while (head != null) {
            ListNode next = head.next;
            head.next = dummy.next;
            dummy.next = head;
            head = next;
        }
        return dummy.next;
    }
	// 解法二
        public ListNode reverseList(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        ListNode newHead = reverseList(head.next);
        head.next.next = head;
        head.next = null;
        return newHead;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

207.课程表

现在你总共有 n 门课需要选，记为 0 到 n-1。

在选修某些课程之前需要一些先修课程。例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]

给定课程总量以及它们的先决条件，判断是否可能完成所有课程的学习？

示例 1:

输入: 2, [[1,0]] 
输出: true
解释: 总共有 2 门课程。学习课程 1 之前，你需要完成课程 0。所以这是可能的。

1
2
3
4

示例 2:

输入: 2, [[1,0],[0,1]]
输出: false
解释: 总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0；并且学习课程 0 之前，你还应先完成课程 1。这是不可能的。

1
2
3
4

说明:

输入的先决条件是由边缘列表表示的图形，而不是邻接矩阵。详情请参见图的表示法。
你可以假定输入的先决条件中没有重复的边。

提示:

这个问题相当于查找一个循环是否存在于有向图中。如果存在循环，则不存在拓扑排序，因此不可能选取所有课程进行学习。
通过 DFS 进行拓扑排序 - 一个关于Coursera的精彩视频教程（21分钟），介绍拓扑排序的基本概念。
拓扑排序也可以通过 BFS 完成。

Solution：

public class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        // 邻接表图
        Map<Integer, List<Integer>> map = new HashMap<>();
        // 保存入度
        int[] degree = new int[numCourses];
        //构建有向图
        for (int[] pre : prerequisites) {
            if (map.containsKey(pre[1])) {
                map.get(pre[1]).add(pre[0]);
            } else {
                map.put(pre[1], new ArrayList<>(Arrays.asList(pre[0])));
            }
            degree[pre[0]]++;
        }
        
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < numCourses; i++) {
            if (degree[i] == 0) {
                queue.offer(i);
            }
        }
        // BFS
        while (!queue.isEmpty()) {
            int i = queue.poll();
            List<Integer> l = map.get(i);
            if(l == null) {
                continue;
            }
            for (int j = 0; j < l.size(); j++) {
                int p = l.get(j);
                degree[p]--;
                if(degree[p] == 0) {
                    queue.offer(p);
                }
            }
        }
        for (int i = 0; i < numCourses; i++) {
            if (degree[i] != 0) {
                return false;
            }
        }
        return true;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

208.实现Trie(前缀树)

题目描述：

实现一个 Trie (前缀树)，包含 insert, search, 和 startsWith 这三个操作。

示例:

Trie trie = new Trie();

trie.insert("apple");
trie.search("apple");   // 返回 true
trie.search("app");     // 返回 false
trie.startsWith("app"); // 返回 true
trie.insert("app");   
trie.search("app");     // 返回 true

1
2
3
4
5
6
7
8
9

说明:

你可以假设所有的输入都是由小写字母 a-z 构成的。
保证所有输入均为非空字符串。

Solution：

public class Trie {
    // 指向所有存在的下一个字符
    private Map<Character, Map> map;

    /**
     * Initialize your data structure here.
     */
    public Trie() {
        map = new HashMap<>();
    }

    /**
     * Inserts a word into the trie.
     */
    public void insert(String word) {
        Map<Character, Map> ws = map;
        for (int i = 0; i < word.length(); i++) {
            ws.putIfAbsent(word.charAt(i), new HashMap<>());
            ws = ws.get(word.charAt(i));
        }
        ws.put('.', null);
    }

    /**
     * Returns if the word is in the trie.
     */
    public boolean search(String word) {
        Map<Character, Map> ws = map;
        for (int i = 0; i < word.length(); i++) {
            ws = ws.get(word.charAt(i));
            if (ws == null) {
                return false;
            }
        }
        return ws.containsKey('.');
    }

    /**
     * Returns if there is any word in the trie that starts with the given prefix.
     */
    public boolean startsWith(String prefix) {
        Map<Character, Map> ws = map;
        for (int i = 0; i < prefix.length(); i++) {
            ws = ws.get(prefix.charAt(i));
            if (ws == null) {
                return false;
            }
        }
        return true;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

215.数组中的第K个最大元素

题目描述：

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:

输入: [3,2,1,5,6,4] 和 k = 2
输出: 5

1
2
3

示例 2:

输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4

1
2
3

说明:

你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

Solution：

public class Solution {
    public int findKthLargest(int[] nums, int k) {
        Queue<Integer> queue = new PriorityQueue<>(Comparator.reverseOrder());
        for (int num : nums) {
            queue.offer(num);
        }
        for (int i = 1; i < k; i++) {
            queue.poll();
        }
        return queue.peek();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

221.最大正方形

题目描述：

在一个由 0 和 1 组成的二维矩阵内，找到只包含 1 的最大正方形，并返回其面积。

示例:

Solution：

public class Solution {
    public int maximalSquare(char[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return 0;
        }
        
        int res = 0;
        int[] heights = new int[matrix[0].length];
        for (int i = 0; i < matrix.length; i++) {
            Stack<Integer> stack = new Stack<>();
            for (int j = 0; j <= heights.length; j++) {
                if (j < heights.length) {
                    heights[j] = (matrix[i][j] == '1') ? 1 + heights[j] : 0;
                }
                int height = (j == heights.length) ? -1 : heights[j];
                while (!stack.isEmpty() && height <= heights[stack.peek()]) {
                    int stackHeight = heights[stack.pop()];
                    int width = stack.isEmpty() ? j : j - stack.peek() - 1;
                    int min = Math.min(width, stackHeight);
                    res = Math.max(res, min * min);
                }
                stack.push(j);
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

226.翻转二叉树

题目描述：

翻转一棵二叉树。

示例：

输入：

     4
   /   \
  2     7
 / \   / \
1   3 6   9

1
2
3
4
5
6

输出：

     4
   /   \
  7     2
 / \   / \
9   6 3   1

1
2
3
4
5
6

备注:
这个问题是受到 Max Howell 的原问题启发的：

谷歌：我们90％的工程师使用您编写的软件(Homebrew)，但是您却无法在面试时在白板上写出翻转二叉树这道题，这太糟糕了。

Solution：

public class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return root;
        }
        
        TreeNode left = root.left;
        root.left = invertTree(root.right);
        root.right = invertTree(left);
        return root;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

234.回文链表

题目描述：

请判断一个链表是否为回文链表。

示例 1:

输入: 1->2
输出: false

1
2
3

示例 2:

输入: 1->2->2->1
输出: true

1
2
3

Solution：

public class Solution {
    public boolean isPalindrome(ListNode head) {
        if (head == null || head.next == null) {
            return true;
        }
        
        // 第一步运用快慢指针找到中间结点
        ListNode slow = head;
        ListNode fast = head;
        while (fast.next != null && fast.next.next != null) {
            fast = fast.next.next;
            slow = slow.next;
        }
        
        // 此时slow即为中间结点，将其后链表逆序
        ListNode secHead = slow.next;
        slow.next = null;
        while (secHead != null) {
            ListNode next = secHead.next;
            secHead.next = slow.next;
            slow.next = secHead;
            secHead = next;
        }
        secHead = slow.next;
        slow.next = null;
        slow = head;
        // 依次比较
        while (slow != null && secHead != null) {
            if (slow.val != secHead.val) {
                return false;
            }
            slow = slow.next;
            secHead = secHead.next;
        }
        return slow == null || slow.next == null;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

236.二叉树的最近公共祖先

题目描述：

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

1
2
3
4

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

1
2
3
4

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。

Solution：

public class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        //  根节点都已经是了还找个屁
        if (root == null || root == p || root == q) {
            return root;
        }
        // 找左边
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        // 找右边
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        // 根节点、左节点、右节点都没有，gg
        if (left == null && right == null) {
            return null;
        }
        // 左节点、右节点都有，证明各1个，此时根节点就是最近公共祖先
        if (left != null && right != null) {
            return root;
        }
        // 都在一边
        return left == null ? right : left;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

238.除自身以外数组的乘积

题目描述：

给定长度为 n 的整数数组 nums，其中 n > 1，返回输出数组 output ，其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

示例:

输入: [1,2,3,4]
输出: [24,12,8,6]

1
2
3

说明: 请**不要使用除法，**且在 O(n) 时间复杂度内完成此题。

Solution：

public class Solution {
    public int[] productExceptSelf(int[] nums) {
        if (nums == null || nums.length == 0) {
            return null;
        }
        
        int[] res = new int[nums.length];
        for (int i = 0, product = 1; i < nums.length; i++) {
            res[i] = product;
            product *= nums[i];
        }
        
        for (int i = nums.length - 1, product = 1; i >= 0; i--) {
            res[i] *= product;
            product *= nums[i];
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

239.滑动窗口的最大值

题目描述：

给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口 k 内的数字。滑动窗口每次只向右移动一位。

返回滑动窗口最大值。

示例:

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7] 
解释: 

  滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

1
2
3
4
5
6
7
8
9
10
11
12
13

注意：

你可以假设 k 总是有效的，1 ≤ k ≤ 输入数组的大小，且输入数组不为空。

Solution：

public class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums == null || nums.length == 0 || k > nums.length) {
            return new int[0];
        }
        
        int[] res = new int[nums.length - k + 1];
        LinkedList<Integer> queue = new LinkedList<>();
        for (int i = 0; i < k - 1; i++) {
            while (!queue.isEmpty() && nums[queue.peekLast()] < nums[i]) {
                queue.pollLast();
            }
            queue.offerLast(i);
        }
        
        for (int i = k - 1; i < nums.length; i++) {
            while (!queue.isEmpty() && nums[queue.peekLast()] < nums[i]) {
                queue.pollLast();
            }
            queue.offerLast(i);
            if (i - queue.peekFirst() >= k) {
                queue.pollFirst();
            }
            res[i - k + 1] = nums[queue.peekFirst()];
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

240.搜索二维矩阵Ⅱ

题目描述：

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

示例:

现有矩阵 matrix 如下：

[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

1
2
3
4
5
6
7
8

给定 target = 5，返回 true。

给定 target = 20，返回 false。

Solution：

public class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return false;
        }
        
        int i = matrix.length - 1;
        int j = 0;
        while (i >= 0 && j < matrix[0].length) {
            if (matrix[i][j] == target) {
                return true;
            }
            
            if (matrix[i][j] > target) {
                i--;
            } else {
                j++;
            }
        }
        return false;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

279.完全平方数

题目描述：

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

示例 1:

输入: n = 12
输出: 3 
解释: 12 = 4 + 4 + 4.

1
2
3
4

示例 2:

输入: n = 13
输出: 2
解释: 13 = 4 + 9.

1
2
3
4

Solution：

public class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n + 1];
        Arrays.fill(dp, Integer.MAX_VALUE);
        for (int i = 1; i * i <= n; i++) {
            dp[i * i] = 1;
        }
        
        for (int i = 1; i < n; i++) {
            for (int j = 0; j * j + i <= n; j++) {
                dp[i + j * j] = Math.min(dp[i + j * j], dp[i] + 1);
            }
        }
        return dp[n];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

283.移动零

题目描述：

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

示例:

输入: [0,1,0,3,12]
输出: [1,3,12,0,0]

1
2
3

说明:

必须在原数组上操作，不能拷贝额外的数组。
尽量减少操作次数。

public class Solution {
    public void moveZeroes(int[] nums) {
        if (nums == null) {
            return;
        }
        
        int k = 0;
        for (int num : nums) {
            if (num != 0) {
                nums[k++] = num;
            }
        }
        
        for (int i = k; i < nums.length; i++) {
            nums[i] = 0;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

287.寻找重复数

题目解析：

给定一个包含 n + 1 个整数的数组 nums，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。假设只有一个重复的整数，找出这个重复的数。

示例 1:

输入: [1,3,4,2,2]
输出: 2

1
2
3

示例 2:

输入: [3,1,3,4,2]
输出: 3

1
2
3

说明：

不能更改原数组（假设数组是只读的）。
只能使用额外的 O(1) 的空间。
时间复杂度小于 O(n2) 。
数组中只有一个重复的数字，但它可能不止重复出现一次。

Solution：

/**
* 把数组看成链表，采用快慢指针法，寻找环的入口
*/
public class Solution {
    public int findDuplicate(int[] nums) {
        int fast = 0;
        int slow = 0;
        while (true) {
            fast = nums[nums[fast]];
            slow = nums[slow];
            if (fast == slow) {
                slow = 0;
                while (nums[fast] != nums[slow]) {
                    fast = nums[fast];
                    slow = nums[slow];
                }
                return nums[slow];
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

297.二叉树的序列化和反序列化

题目描述：

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

示例:

你可以将以下二叉树：

    1
   / \
  2   3
     / \
    4   5

序列化为 "[1,2,3,null,null,4,5]"

1
2
3
4
5
6
7
8
9
10

提示: 这与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，你也可以采用其他的方法解决这个问题。

说明: 不要使用类的成员 / 全局 / 静态变量来存储状态，你的序列化和反序列化算法应该是无状态的。

Soution：

public class Codec {
    private int index = -1;

    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        if (root == null) {
            return "#,";
        }
        
        StringBuilder sb = new StringBuilder();
        sb.append(root.val).append(',').append(serialize(root.left)).append(serialize(root.right));
        return sb.toString();
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        if (data == null) {
            return null;
        }
        return helper(data.split(","));
    }
    
    private TreeNode helper(String[] strs) {
        index++;
        if ("#".equals(strs[index])) {
            return null;
        }
        TreeNode node = new TreeNode(Integer.valueOf(strs[index]));
        node.left = helper(strs);
        node.right = helper(strs);
        return node;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

300.最长上升子序列

题目描述：

给定一个无序的整数数组，找到其中最长上升子序列的长度。

示例:

输入: [10,9,2,5,3,7,101,18]
输出: 4 
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

1
2
3
4

说明:

可能会有多种最长上升子序列的组合，你只需要输出对应的长度即可。
你算法的时间复杂度应该为 O(n2) 。

Solution：

public class Solution {
    public int lengthOfLIS(int[] nums) {
        if (nums == null || nums.length == 0) {
            return 0;
        }
        
        // dp[i]表示以nums中第i个元素结尾的最长上升子序列长度
        int[] dp = new int[nums.length];
        int res = 1;
        Arrays.fill(dp, 1);
        for (int i = 0; i < nums.length; i++) {
            for (int j = 0; j <= i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[j] + 1, dp[i]);
                    res = Math.max(res, dp[i]);
                }
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

309.最佳买卖股票时期含冷冻期

题目描述：

给定一个整数数组，其中第 i 个元素代表了第 i 天的股票价格。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

示例:

输入: [1,2,3,0,2]
输出: 3 
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
1
2
3

Solution：

public class Solution {
    public int maxProfit(int[] prices) {
        if (prices == null || prices.length < 2) {
            return 0;
        }
        int buy = Integer.MIN_VALUE;
        int sale = 0;
        int rest = 0;
        for (int price : prices) {
            int salePre = sale;
            int buyPre = buy;
            sale = Math.max(buy + price, sale);// 卖或者冻结
            buy = Math.max(buy, rest - price); // 什么都不干或者卖
            rest = Math.max(rest, Math.max(salePre, buy));
        }
        return sale;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

312.戳气球

有 n 个气球，编号为0 到 n-1，每个气球上都标有一个数字，这些数字存在数组 nums 中。

现在要求你戳破所有的气球。每当你戳破一个气球 i 时，你可以获得 nums[left] * nums[i] * nums[right] 个硬币。这里的 left 和 right 代表和 i 相邻的两个气球的序号。注意当你戳破了气球 i 后，气球 left 和气球 right 就变成了相邻的气球。

求所能获得硬币的最大数量。

说明:

你可以假设 nums[-1] = nums[n] = 1，但注意它们不是真实存在的所以并不能被戳破。
0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100

示例:

输入: [3,1,5,8]
输出: 167 
解释: nums = [3,1,5,8] --> [3,5,8] -->   [3,8]   -->  [8]  --> []
     coins =  3*1*5      +  3*5*8    +  1*3*8      + 1*8*1   = 167
1
2
3
4

Solution：

public class Solution {
    public int maxCoins(int[] iNums) {
        int n = iNums.length;
        int[] nums = new int[n + 2];
        for (int i = 0; i < n; i++) {
            nums[i + 1] = iNums[i];
        }
        nums[0] = nums[n + 1] = 1;
        // dp[i][j]表示戳爆[i, j]区间气球得到的最大硬币个数
        int[][] dp = new int[n + 2][n + 2];
        for (int k = 1; k <= n; k++) { // k表示长度
            for (int i = 1; i <= n - k + 1; i++) {// i表示起始位置
                int j = i + k - 1; // j表示结束位置
                for (int x = i; x <= j; x++) {
                    // 戳爆 [i, x - 1] 、 x 、 [x + 1, j] 
                    dp[i][j] = Math.max(dp[i][j], dp[i][x - 1] + nums[i - 1] * nums[x] * nums[j + 1] + dp[x + 1][j]);
                }
            }
        }
        return dp[1][n];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

322.零钱兑换

题目描述：

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

示例 1:

输入: coins = [1, 2, 5], amount = 11
输出: 3 
解释: 11 = 5 + 5 + 1

1
2
3
4

示例 2:

输入: coins = [2], amount = 3
输出: -1

1
2
3

说明:
你可以认为每种硬币的数量是无限的。

Solution：

public class Solution {
    public int coinChange(int[] coins, int amount) {
        if (coins == null || coins.length == 0 || amount < 0) {
            return -1;
        }
        
        int res = 0;
        int[] dp = new int[amount + 1];
        for (int i = 1; i <= amount; i++) {
            dp[i] = amount + 1;
            for (int j = 0; j < coins.length; j++) {
                if (i >= coins[j]) {
                    dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);
                }
            }
        }
        return dp[amount] > amount ? -1 : dp[amount];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

337.打家劫舍Ⅲ

题目描述：

在上次打劫完一条街道之后和一圈房屋后，小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为“根”。除了“根”之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。如果两个直接相连的房子在同一天晚上被打劫，房屋将自动报警。

计算在不触动警报的情况下，小偷一晚能够盗取的最高金额。

示例 1:

输入: [3,2,3,null,3,null,1]

     3
    / \
   2   3
    \   \ 
     3   1

输出: 7 
解释: 小偷一晚能够盗取的最高金额 = 3 + 3 + 1 = 7.

1
2
3
4
5
6
7
8
9
10
11

示例 2:

输入: [3,4,5,1,3,null,1]

     3
    / \
   4   5
  / \   \ 
 1   3   1

输出: 9
解释: 小偷一晚能够盗取的最高金额 = 4 + 5 = 9.
1
2
3
4
5
6
7
8
9
10

Solution：

public class Solution {
    public int rob(TreeNode root) {
        int[] res = helper(root);
        return Math.max(res[0], res[1]);
    }
    
    private int[] helper(TreeNode root) {
        int[] res = new int[2];
        if (root == null) {
            return res;
        }
        int[] left = helper(root.left);
        int[] right = helper(root.right);
        res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]); // 不打劫当前节点
        res[1] = root.val + left[0] + right[0]; // 打劫当前节点和左右子树的子树
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

338.比特位计数

题目描述：

给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ，计算其二进制数中的 1 的数目并将它们作为数组返回。

示例 1:

输入: 2
输出: [0,1,1]

1
2
3

示例 2:

输入: 5
输出: [0,1,1,2,1,2]

1
2
3

Solution：

public class Solution {
    public int[] countBits(int num) {
        int[] res = new int[num + 1];
        for (int i = 1; i <= num; i++) {
            // 将i表示的二进制数的最后一位1变成0即为 i & (i - 1)
            res[i] = res[i & (i - 1)] + 1;
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10

347.前K个高频元素

题目描述：

给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

示例 1:

输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

1
2
3

示例 2:

输入: nums = [1], k = 1
输出: [1]

1
2
3

说明：

你可以假设给定的 k 总是合理的，且 1 ≤ k ≤ 数组中不相同的元素的个数。
你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。

Solution：

public class Solution {
    public List<Integer> topKFrequent(int[] nums, int k) {
        List<Integer> res = new ArrayList<>();
        if (nums == null || nums.length == 0 || k <= 0) {
            return res;
        }
        Map<Integer, Integer> map = new HashMap<>();
        for (int num : nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }
        Queue<Integer> queue = new PriorityQueue<>(((o1, o2) -> map.get(o2) - map.get(o1)));
        for (Integer key : map.keySet()) {
            queue.offer(key);
        }
        for (int i = 0; i < k; i++) {
            res.add(queue.poll());
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

394.字符串解码

题目描述：

给定一个经过编码的字符串，返回它解码后的字符串。

编码规则为: k[encoded_string]，表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。

你可以认为输入字符串总是有效的；输入字符串中没有额外的空格，且输入的方括号总是符合格式要求的。

此外，你可以认为原始数据不包含数字，所有的数字只表示重复的次数 k ，例如不会出现像 3a 或 2[4] 的输入。

示例:

s = "3[a]2[bc]", 返回 "aaabcbc".
s = "3[a2[c]]", 返回 "accaccacc".
s = "2[abc]3[cd]ef", 返回 "abcabccdcdcdef".
1
2
3

Solution：

public class Solution {
    private int i = 0;
    
    public String decodeString(String s) {
        if (s == null || s.length() == 0) {
            return "";
        }
        
        StringBuilder sb = new StringBuilder();
        for (; i < s.length() && s.charAt(i) != ']'; i++) {
            if ((s.charAt(i) >= 'a' && s.charAt(i) <= 'z') || (s.charAt(i) >= 'A' && s.charAt(i) <= 'Z')) {
                sb.append(s.charAt(i));
                continue;
            }
            int count = 0;
            while (s.charAt(i) <= '9' && s.charAt(i) >= '0') {
                count = count * 10 + s.charAt(i++) - '0';
            }
            i++; // 越过'['或
            String temp = decodeString(s);
            while (count-- > 0) {
                sb.append(temp);
            }
        }
        return sb.toString();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

406.根据身高重建队列

题目描述：

假设有打乱顺序的一群人站成一个队列。每个人由一个整数对(h, k)表示，其中h是这个人的身高，k是排在这个人前面且身高大于或等于h的人数。编写一个算法来重建这个队列。

注意：
总人数少于1100人。

示例

输入:
[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]

输出:
[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]
1
2
3
4
5

Solution：

public class Solution {
    public int[][] reconstructQueue(int[][] people) {
        if (people == null || people.length == 0 || people[0].length == 0) {
            return new int[0][0];
        }
        
        Arrays.sort(people, (o1, o2) -> o1[0] == o2[0] ? o1[1] - o2[1] : o2[0] - o1[0]);
        List<int[]> list = new ArrayList<>();
        for (int[] i : people) {
            list.add(i[1], i);
        }
        return list.toArray(new int[list.size()][]);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

416.分割等和子集

题目描述：

给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

注意:

每个数组中的元素不会超过 100
数组的大小不会超过 200

示例 1:

输入: [1, 5, 11, 5]

输出: true

解释: 数组可以分割成 [1, 5, 5] 和 [11].

1
2
3
4
5
6

示例 2:

输入: [1, 2, 3, 5]

输出: false

解释: 数组不能分割成两个元素和相等的子集.
1
2
3
4
5

Solution:

public class Solution {
    public boolean canPartition(int[] nums) {
        if (nums == null || nums.length == 0) {
            return true;
        }
        
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        if ((sum & 1) == 1) {
            return false;
        }
        int c = (sum >> 1) + 1;
        // dp[i] 表示nums能否装下容量为i的背包
        boolean[] dp = new boolean[c];
        dp[0] = true;
        for (int i = 1; i < nums.length; i++) {
            for (int j = c - 1; j >= nums[i]; j--) {
                dp[j] = dp[j] || dp[j - nums[i]];
            }
        }
        return dp[c - 1];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

437.路径总和Ⅲ

题目描述：

给定一个二叉树，它的每个结点都存放着一个整数值。

找出路径和等于给定数值的路径总数。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

二叉树不超过1000个节点，且节点数值范围是 [-1000000,1000000] 的整数。

示例：

root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8

      10
     /  \
    5   -3
   / \    \
  3   2   11
 / \   \
3  -2   1

返回 3。和等于 8 的路径有:

1.  5 -> 3
2.  5 -> 2 -> 1
3.  -3 -> 11
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Solution：

public class Solution {
    public int pathSum(TreeNode root, int sum) {
        if (root == null) {
            return 0;
        }

        return pathSumCount(root, sum)
                + pathSum(root.left, sum)
                + pathSum(root.right, sum);
    }

    public int pathSumCount(TreeNode root, int sum) {
        if (root == null) {
            return 0;
        }

        return (root.val == sum ? 1 : 0)
                + pathSumCount(root.left, sum - root.val)
                + pathSumCount(root.right, sum - root.val);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

438.找到字符串中所有字母异位词

题目描述：

给定一个字符串 s 和一个非空字符串 p，找到 s 中所有是 p 的字母异位词的子串，返回这些子串的起始索引。

字符串只包含小写英文字母，并且字符串 s 和 p 的长度都不超过 20100。

说明：

字母异位词指字母相同，但排列不同的字符串。
不考虑答案输出的顺序。

示例 1:

输入:
s: "cbaebabacd" p: "abc"

输出:
[0, 6]

解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的字母异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的字母异位词。

1
2
3
4
5
6
7
8
9
10

示例 2:

输入:
s: "abab" p: "ab"

输出:
[0, 1, 2]

解释:
起始索引等于 0 的子串是 "ab", 它是 "ab" 的字母异位词。
起始索引等于 1 的子串是 "ba", 它是 "ab" 的字母异位词。
起始索引等于 2 的子串是 "ab", 它是 "ab" 的字母异位词。
1
2
3
4
5
6
7
8
9
10

Solution：

public class Solution {
    public List<Integer> findAnagrams(String s, String p) {
        List<Integer> res = new ArrayList<>();
        if (s == null || p == null || s.length() < p.length()) {
            return res;
        }
        int[] map = new int[26];
        for (int i = 0; i < p.length(); i++) {
            map[p.charAt(i) - 'a']++;
        }
        int count = p.length();
        int l = 0;
        int r = 0;
        while (r < s.length()) {
            if (map[s.charAt(r++) - 'a']-- > 0) {
                count--;
            }
            if (count == 0) {
                res.add(l);
            }
            if (r - l == p.length()) {
                if (map[s.charAt(l++) - 'a']++ >= 0) {
                    count++;
                }
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

448.找到所有数组中消失的数字

题目描述：

给定一个范围在 1 ≤ a[i] ≤ n ( n = 数组大小 ) 的整型数组，数组中的元素一些出现了两次，另一些只出现一次。

找到所有在 [1, n] 范围之间没有出现在数组中的数字。

您能在不使用额外空间且时间复杂度为*O(n)*的情况下完成这个任务吗? 你可以假定返回的数组不算在额外空间内。

示例:

输入:
[4,3,2,7,8,2,3,1]

输出:
[5,6]
1
2
3
4
5

Solution：

public class Solution {
    public List<Integer> findDisappearedNumbers(int[] nums) {
        List<Integer> res = new ArrayList<>();
        if (nums == null || nums.length == 0) {
            return res;
        }
        for (int i = 0; i < nums.length; i++) {
            if (nums[Math.abs(nums[i]) - 1] > 0) {
                nums[Math.abs(nums[i]) - 1] *= -1;
            }
        }
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] > 0) {
                res.add(i + 1);
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

461.汉明距离

题目描述：

两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。

给出两个整数 x 和 y，计算它们之间的汉明距离。

注意：
0 ≤ x, y < 231.

示例:

输入: x = 1, y = 4

输出: 2

解释:
1   (0 0 0 1)
4   (0 1 0 0)
       ↑   ↑

上面的箭头指出了对应二进制位不同的位置。
1
2
3
4
5
6
7
8
9
10

Solution：

public class Solution {
    public int hammingDistance(int x, int y) {
        int res = 0;
        int temp =  x ^ y;
        while (temp != 0) {
            res += temp & 1;
            temp >>>= 1;
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11

494.目标和

题目描述：

给定一个非负整数数组，a1, a2, …, an, 和一个目标数，S。现在你有两个符号 + 和 -。对于数组中的任意一个整数，你都可以从 + 或 -中选择一个符号添加在前面。

返回可以使最终数组和为目标数 S 的所有添加符号的方法数。

示例 1:

输入: nums: [1, 1, 1, 1, 1], S: 3
输出: 5
解释: 

-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3

一共有5种方法让最终目标和为3。

1
2
3
4
5
6
7
8
9
10
11
12

注意:

数组的长度不会超过20，并且数组中的值全为正数。
初始的数组的和不会超过1000。
保证返回的最终结果为32位整数。

Solution：

public class Solution {
    private int res = 0;
    
    public int findTargetSumWays(int[] nums, int S) {
        helper(nums, 0, S);
        return res;
    }
    
    private void helper(int[] nums, int index, int S) {
        if (index == nums.length) {
            if (S == 0) {
                res++;
            }
            return;
        }
        helper(nums, index + 1, S - nums[index]);
        helper(nums, index + 1, S + nums[index]);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

538.把二叉搜索树转换为累加树

题目描述：

给定一个二叉搜索树（Binary Search Tree），把它转换成为累加树（Greater Tree)，使得每个节点的值是原来的节点值加上所有大于它的节点值之和。

例如：

输入: 二叉搜索树:
              5
            /   \
           2     13

输出: 转换为累加树:
             18
            /   \
          20     13
1
2
3
4
5
6
7
8
9

Solution：

/**
 * 按照 右子树 -> 根节点 ->  左子树 的顺序遍历，统计之前节点值的和，加到当前节点上
 */
public class Solution {
    public TreeNode convertBST(TreeNode root) {
        if (root == null) {
            return null;
        }

        int sum = 0;
        Stack<TreeNode> stack = new Stack<>();
        TreeNode node = root;
        while (!stack.isEmpty() || node != null) {
            while (node != null) {
                stack.push(node);
                node = node.right;
            }
            node = stack.pop();
            int val = node.val;
            node.val += sum;
            sum += val;
            node = node.left;
        }
        return root;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

543.二叉树的直径

题目描述：

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过根结点。

示例 :
给定二叉树

返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

**注意：**两结点之间的路径长度是以它们之间边的数目表示。

Solution：

public class Solution {
    private int res = 0;
    
    public int diameterOfBinaryTree(TreeNode root) {
        helper(root);
        return res;
    }
    
    private int helper(TreeNode root) {
        if (root == null) {
            return 0;
        }
        
        int left = helper(root.left);
        int right = helper(root.right);
        res = Math.max(res, left + right);
        return 1 + Math.max(left, right);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

560.和为K的子数组

题目描述：

给定一个整数数组和一个整数 **k，**你需要找到该数组中和为 k 的连续的子数组的个数。

示例 1 :

输入:nums = [1,1,1], k = 2
输出: 2 , [1,1] 与 [1,1] 为两种不同的情况。

1
2
3

说明 :

数组的长度为 [1, 20,000]。
数组中元素的范围是 [-1000, 1000] ，且整数 k 的范围是 [-1e7, 1e7]。

Solution：

public class Solution {
    public int subarraySum(int[] nums, int k) {
        if (nums == null || nums.length <= 0) {
            return 0;
        }
        
        int res = 0;
        Map<Integer, Integer> map = new HashMap<>();
        map.put(0, 1);
        int sum = 0;
        
        for (int num : nums) {
            sum += num;
            // map.get(sum - k)表示从头开始，和为 sum - k的子数组个数
            // 那么子数组后面到当前位置的元素和即为 sum - (sum - k) = k
            res += map.getOrDefault(sum - k, 0);
            map.put(sum, map.getOrDefault(sum, 0) + 1);
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

572.另一个树的子树

题目描述：

给定两个非空二叉树 s 和 t，检验 s 中是否包含和 t 具有相同结构和节点值的子树。s 的一个子树包括 s 的一个节点和这个节点的所有子孙。s 也可以看做它自身的一棵子树。

示例 1:
给定的树 s:

给定的树 t：

返回 true，因为 t 与 s 的一个子树拥有相同的结构和节点值。

示例 2:
给定的树 s：

给定的树 t：

返回 false。

Solution：

public class Solution {
    public boolean isSubtree(TreeNode s, TreeNode t) {
        if (s == null && t == null) {
            return true;
        }
        if (s == null || t == null) {
            return false;
        }
        return isSametree(s, t)
                || isSubtree(s.left, t)
                || isSubtree(s.right, t);
    }

    private boolean isSametree(TreeNode s, TreeNode t) {
        if (s == null && t == null) {
            return true;
        }
        if (s == null || t == null) {
            return false;
        }
        return s.val == t.val && isSametree(s.left, t.left) && isSametree(s.right, t.right);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

581.最短无序连续子数组

题目描述：

给定一个整数数组，你需要寻找一个连续的子数组，如果对这个子数组进行升序排序，那么整个数组都会变为升序排序。

你找到的子数组应是最短的，请输出它的长度。

示例 1:

输入: [2, 6, 4, 8, 10, 9, 15]
输出: 5
解释: 你只需要对 [6, 4, 8, 10, 9] 进行升序排序，那么整个表都会变为升序排序。

1
2
3
4

说明 :

输入的数组长度范围在 [1, 10,000]。
输入的数组可能包含重复元素，所以升序的意思是**<=。**

Solution：

public class Solution {
    public int findUnsortedSubarray(int[] nums) {
        if (nums == null || nums.length < 2) {
            return 0;
        }
        
        int min = nums[nums.length - 1];
        int max = nums[0];
        int start = 0;
        int end = -1;
        for (int i = 1; i < nums.length; i++) {
            if (max > nums[i]) {
                end = i;
            } else {
                max = nums[i];
            }
            
            if (min < nums[nums.length - i - 1]) {
                start = nums.length - i - 1;
            } else {
                min = nums[nums.length - i - 1];
            }
        }
        return end - start + 1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

617.合并二叉树

题目描述：

给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。

你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

示例 1:

输入: 
	Tree 1                     Tree 2                  
          1                         2                             
         / \                       / \                            
        3   2                     1   3                        
       /                           \   \                      
      5                             4   7                  
输出: 
合并后的树:
	     3
	    / \
	   4   5
	  / \   \ 
	 5   4   7
1
2
3
4
5
6
7
8
9
10
11
12
13
14

Solution：

public class Solution {
    public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
        if (t1 == null || t2 == null) {
            return t1 != null ? t1 : t2;
        }
        
        t1.val += t2.val;
        t1.left = mergeTrees(t1.left, t2.left);
        t1.right = mergeTrees(t1.right, t2.right);
        return t1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

647.回文子串

题目描述：

给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被计为是不同的子串。

示例 1:

输入: "abc"
输出: 3
解释: 三个回文子串: "a", "b", "c".
1
2
3

示例 2:

输入: "aaa"
输出: 6
说明: 6个回文子串: "a", "a", "a", "aa", "aa", "aaa".
1
2
3

注意:

输入的字符串长度不会超过1000。

Solution：

public class Solution {
    private int res = 0;

    public int countSubstrings(String s) {
        if (s == null || s.length() < 1) {
            return 0;
        }

        for (int i = 0; i < s.length(); i++) {
            find(s, i, i);
            find(s, i, i + 1);
        }
        return res;
    }

    private void find(String s, int i, int j) {
        while (i >= 0 && i < s.length() && j >= 0 && j < s.length() && s.charAt(i--) == s.charAt(j++)) {
            res++;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

771.宝石与石头

题目描述：

给定字符串J 代表石头中宝石的类型，和字符串 S代表你拥有的石头。 S 中每个字符代表了一种你拥有的石头的类型，你想知道你拥有的石头中有多少是宝石。

J 中的字母不重复，J 和 S中的所有字符都是字母。字母区分大小写，因此"a"和"A"是不同类型的石头。

示例 1:

输入: J = "aA", S = "aAAbbbb"
输出: 3

1
2
3

示例 2:

输入: J = "z", S = "ZZ"
输出: 0

1
2
3

注意:

S 和 J 最多含有50个字母。
J 中的字符不重复。

Solution：

public class Solution {
    public int numJewelsInStones(String J, String S) {
        int res = 0;
        Set<Character> set = new HashSet<>();
        for (int i = 0; i < J.length(); i++) {
            set.add(J.charAt(i));
        }
        for (int i = 0; i < S.length(); i++) {
            if (set.contains(S.charAt(i)))
                res++;
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/我家自动化/article/detail/117837

Leetcode Top100题目和答案（Java完整版 面试必备）_leetcode答案 java

文章目录

1.两数之和

2.两数相加

3.无重复字符的最长子串

4.寻找两个有序数组的中位数

5.最长回文子串

10.正则表达式匹配

11.盛最多水的容器

15.三数之和

17.电话号码的字母组合

19.删除链表的倒数第N个节点

20有效的括号

21.合并两个有序链表

22.生成括号

23.合并K个排序链表

31.下一个排列

32.最长有效括号

33.搜索旋转排序数组

34.在排序数组中查找元素的第一个和最后一个位置

39.组合总和

42.接雨水

46.全排列

48.旋转图像

49.字母异位词分组

53.最大子序和

55.跳跃游戏

56.合并区间

62.不同路径

64.最小路径和

70.爬楼梯

72.编辑距离

75.颜色分类

76.最小覆盖子串

78.子集

79.单词搜索

84.柱状图中最大的矩形

85.最大矩形

94.二叉树的中序遍历

96.不同的二叉搜索树

98.验证二叉搜索树

101.对称二叉树

102.二叉树的层序遍历

104.二叉树的最大深度

105.从前序遍历和中序遍历序列构造二叉树

114.二叉树展开为链表

121.买卖股票的最佳时机

124.二叉树中的最大路径和

128.最长连续序列

136.只出现一次的数字

139.单词拆分

141.环形链表

142.环形链表Ⅱ

146.LRU缓存机制

148.排序链表

152.乘机最大子序列

155.最小栈

160.相交链表

169.求众数

198.打家劫舍

200.岛屿的个数

206.反转链表

207.课程表

208.实现Trie(前缀树)

215.数组中的第K个最大元素

221.最大正方形

226.翻转二叉树

234.回文链表

236.二叉树的最近公共祖先

238.除自身以外数组的乘积

239.滑动窗口的最大值

240.搜索二维矩阵Ⅱ

279.完全平方数

283.移动零

287.寻找重复数

297.二叉树的序列化和反序列化

300.最长上升子序列

309.最佳买卖股票时期含冷冻期

312.戳气球

322.零钱兑换

Leetcode Top100题目和答案（Java完整版面试必备）_leetcode答案 java