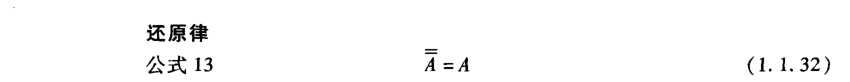逻 辑 代 数 的 基 本 概 念 、 公 式 和 定 理_逻辑代数

1.1.1 基本和常用逻辑运算

在逻辑代数中，基本逻辑运算有与、或、非三种，常用的逻辑运算是与非、或非、与或非、异或等。

一、三种基本逻辑运算

1、基本逻辑关系举例

根据电路中的有关定理，可以很容易的列出表1.1.1表示的功能表。
(2)真值表
在图1.1.1中，经过设定变量和状态赋值之后，便可以得到反映开关状态与电灯亮灭之间因果关系的数学表达形式——逻辑真值表，简称真值表。

·设定变量

用英文字母表示开关和电灯的过程，称为设定变量。现用A、B、Y,Y2、Y3分别表示开关A、B和灯Y1、Y2、Y3。

·状态赋值

用0和1分别表示开关和电灯有关状态的过程，称为状态赋值。现用0表示开关断开和灯灭，用1表示开关闭合和灯亮。这也称为变量取值。

列真值表

根据设定变量和状态赋值情况，由表1.1.1所示的功能表，可以很容易地列出如表1.1.2所示的表格，这种表一般称为真值表。
(3)三种基本逻辑关系

·与逻辑关系

当决定一件事情的各个条件全部具备时，这件事情才会发生，这样的因果关系称为与逻辑关系。
在图1.1.1(a)中，只有开关A与开关B都闭合时，灯Y1才会亮，所以对灯Y1亮这件事情来说，开关A、开关B闭合是与的逻辑关系。

·或逻辑关系

当决定一件事情的各个条件中，只要有一个具备，这件事情就会发生，这样的因果关系称为或逻辑关系。
在图1.1.1(b)中，只要开关A或者开关B闭合，灯Y2就会亮，所以对灯Y2亮这件事情来说，开关A、开关B闭合是或的逻辑关系。

·非逻辑关系

非就是反，就是否定。
在图1.1.1©中，当开关A断开时，灯Y3亮，闭合时反而会灭，所以对灯Y亮来说，开关闭合是一种非的逻辑关系。”

2.基本逻辑运算

(1)与运算

在表1.1.2中，对Y1来说，只有当A与B均为1时，其值才会为1,这显然是一种与的逻辑关系，并记作

  Y1=A·B                                   (1.1.1)
1

读作Y1等于A与B,相应地将这种运算称为逻辑与运算，简称与运算。与运算和算术中的乘法运算是一样的，所以又称为逻辑乘法运算，相应地，式（1.1.1)又可读作Y1等于A乘B。书写时表示与或者乘的符号“。”常省略。

(2)或运算

在表1.1.2中，对Y2来说，只要A或B为1时，其值就会为1,这显然是一种或的逻辑关系，并记作

Y2=A+B										(1.1.2)
1

读作Y2等于A或B,相应地，将这种运算称为逻辑或运算，简称或运算。或运算和算术中的加法运算很相似，所以又称为逻辑加法运算，相应地，式（1.1.2)又常读作Y2等于A加B。

(3)非运算

在表1.1.2中，当A取值为0时Y3为1,A取值为1时Y,反而为0,这显然是一种逻辑非关系，并记作

Y3=A-  										(1.1.3)
1

读作Y,等于A非，或者Y,等于A反。A上面的一横就表示非或者反。相应地，将这种运算称为逻辑非运算或逻辑反运算，简称非或者反运算。

**二、逻辑变量与逻辑函数及几种常用逻辑运算

1.逻辑变量与逻辑函数

(1)逻辑变量**

在逻辑代数中，和普通代数一样，也是用英文字母表示变量，称为逻辑变量。不过其取值十分简单，在二值逻辑中，不是1就是0,没有第三种可能。而且，这里的0和1没有数值大小的含义，所表示的是事物相互对立而又联系着的两个方面，即两种状态。例如，图1.1.1中开关的断开与闭合、电灯的灭与亮等。

(2)逻辑函数

式（1.1.1)~(1.1.3)称为逻辑表达式，式中A、B称为输入逻辑变量，Y1、Y2、Y,称为输出逻辑变量，字母上面无反号的称为原变量，有反号的称为反变量。三个表达式准确地描述了与、或、非三种基本逻辑关系。在式（1.1.1)中，变量A、B之间是与的逻辑关系，Y1是A和B的与函数；在式（1.1.2)中，A、B之间是或的逻辑关系，Y2是A和B的或函数；在式（1.1.3)中，Y3是A的反函数。

一般地说，如果输入逻辑变量A、B、…的取值确定之后，输出逻辑变量Y的值也被唯一地确定了，那么就称Y是A、B、…的逻辑函数，并写为

Y=F(A,B,...)
1

一般情况下，常用真值表描述变量取值和函数值之间的对应关系。由于在二值逻辑中，变量和函数的取值都只有0、1两种可能，十分简单，所以可用穷举的方法，把变量的各种可能取值和相应的函数值，以表格形式全部列出来，来表示变量与函数之间的关系，这种表格就称为真值表。表1.1.2所示是最简单的例子。

2**.几种常用的逻辑运算**

在逻辑代数中，除了与、或、非三种基本逻辑运算外，经常用到的还有由这三种基本运算构成的一些复合运算。

(1)与非运算		Y4=（A·B）-				(1.1.4)

(2)或非运算		Y5=（A+B）-				(1.1.5)

(3)与或非运算	Y6=（A·B+C·D）-			(1.1.6)

(4)异或运算     Y1=（A·B+A·B=A+B）-			(1.1.7)
1
2
3
4
5
6
7

三、基本和常用逻辑运算的逻辑符号

在数字电路中，基本和常用逻辑运算的应用十分广泛，它们是构成各种复杂逻辑运算的基础，因此都有实现这些运算的称之为门电路的逻辑电路存在，而它们也是组成各种数字电路的基本单元。图1.1.2给出的就是实现基本和常用逻辑运算的逻辑符号。
需要特别说明的是，逻辑符号不能主观脑造。图1.1.2给出的符号都有具逻辑电路器件存在，在市场上可以买到的 。

1.1.2 公式和定理