STL容器 —— bitset

前言： STL是提供了位图的容器的，那就是 bitset。本篇博客的任务就是 认识位图算法；了解一下STL中bitset的接口函数，并模拟实现bitset；最后用位图去解决三个常见的数据处理问题。

---

1. 认识位图算法

位图的应用非常的广泛，它的出现使得处理数据变得更加的高效，节省空间。

举个例子： 想必大家都打过王者，王者的用户数据非常的庞大，比如要新建立一个用户，你得起个用户名，用户名不能和他人的重复，这底层是如何实现的？那么多的用户，系统是如何判定你起的用户名没用和他人的重复？并且王者还得保存你的登录信息，假如你很久没有登录王者，你某一天闲着登录了一下，王者界面会提示你 ：老玩家，你已经有88天没有登录王者了，这里提供了老玩家回归礼包。王者后台是如何确定你多久没登录的？

答案是 ：利用位图算法。

在面对大量庞大数据的处理时，我们多用位图来处理。上面例子中，起用户名不重复，直接用位图去处理还不行，因为用户名不能直接转化成整数，这得用布隆过滤器这种办法来处理次情况。但是登录信息是可以直接用位图处理的。

比如：我创建一个char类型，它是8个比特位。分别代表周日，周一，周二，……周六。

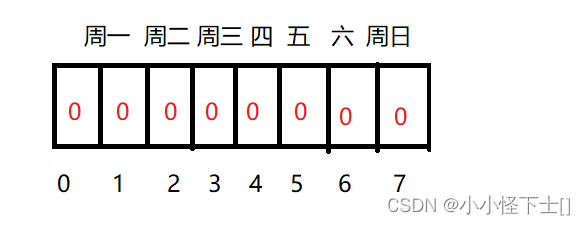
如果在星期一登录了，那就将周一的位置 设置为 1，简言之，为一就表明登录，为零就表明没有登录。

比如：下图就表明一周登录了 3天。

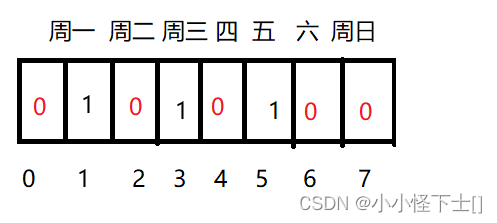
就类似这样，用O(1)的时间，就能查出那一天登录了。

位图的应用很广泛，这里不一 一介绍，接下来我们来学习STL中的bitset。

---

2. STL中的bitset

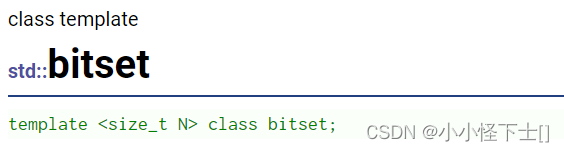
可以看到它是有模板参数的，用的是一个非类型模板参数 N，来表示开多大的位图空间。

2.1 构造函数

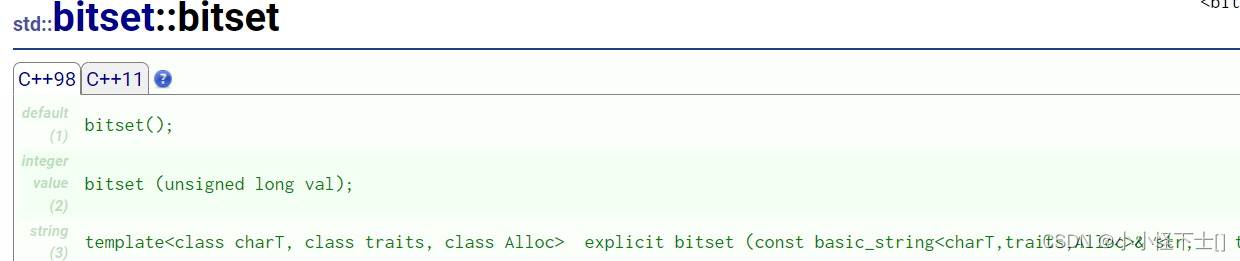
第一个是构造空的位图，默认所有位都是0；
第二个是给定值，初始化位图；
第三个是给一个字符串对象，来初始化位图

int main()
{
    std::bitset<16> foo;
	std::bitset<16> bar(0xfa2);
	std::bitset<16> baz("0101111001");

	std::cout << "foo: " << foo << '\n';
	std::cout << "bar: " << bar << '\n';
	std::cout << "baz: " << baz << '\n';
return 0;
}
1
2
3
4
5
6
7
8
9
10
11

运行结果：

---

2.2 运算符重载

bitset支持的运算符重载有：

• ^=，&=，|=，<<=，>>=，==，!=
• ~，|，&， ^;
• <<，>>(左移位，右移位)
• <<，>>(流提取，流插入)

int main()
{
  std::bitset<4> foo (std::string("1001"));
  std::bitset<4> bar (std::string("0011"));

  std::cout << (foo^=bar) << '\n';       // 1010 (XOR,assign)
  std::cout << (foo&=bar) << '\n';       // 0010 (AND,assign)
  std::cout << (foo|=bar) << '\n';       // 0011 (OR,assign)

  std::cout << (foo<<=2) << '\n';        // 1100 (SHL,assign)
  std::cout << (foo>>=1) << '\n';        // 0110 (SHR,assign)

  std::cout << (~bar) << '\n';           // 1100 (NOT)
  std::cout << (bar<<1) << '\n';         // 0110 (SHL)
  std::cout << (bar>>1) << '\n';         // 0001 (SHR)

  std::cout << (foo==bar) << '\n';       // false (0110==0011)
  std::cout << (foo!=bar) << '\n';       // true  (0110!=0011)

  std::cout << (foo&bar) << '\n';        // 0010
  std::cout << (foo|bar) << '\n';        // 0111
  std::cout << (foo^bar) << '\n';        // 0101
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

程序运行结果：

---

2.3 访问位图

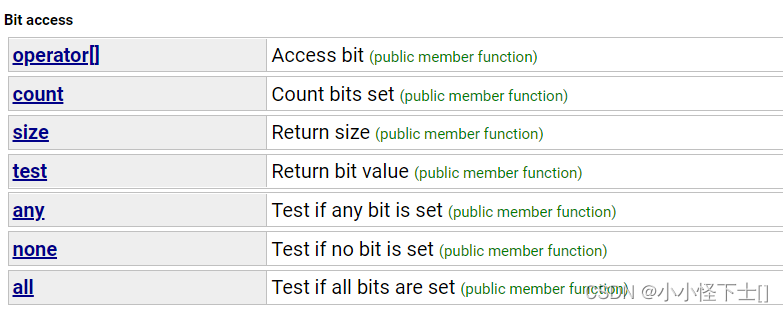
• 位图的底层是vector，所以它也支持的 [] 。

• count是 计算位图中 1 的个数；size是位图的大小；

• test 很重要，它用于判断位图中某个位置是否为1；

• all 也是用于判断位图中是否有 1 ，但是它不是判断某个位置，它是判断位图中的所有位置，如果位图中都是 1 ，那它返回 true，否则返回 false；

• none和all恰好相反，位图中 全为0 返回true，否则返回false；

• any 是只要位图中 有 1，就返回 ture，否则返回 false；

我们着重测试一下：test

int mian()
{
  std::bitset<5> foo (std::string("01011"));

  std::cout << "foo contains:\n";
  std::cout << std::boolalpha;
  for (std::size_t i=0; i<foo.size(); ++i)
    std::cout << foo.test(i) << '\n';
    
 return 0;
}
1
2
3
4
5
6
7
8
9
10
11

2.4 位图的操作

• set 可以将所有位置设置为1，也可以将某个位置设置0或者1；
• reset 可以将所有位置设置为0，也可以将某个位置设置0；
• flip 可以将位图中的数据按位取反，也可以将某个位置按位取反；
• 还有几个转换操作，将位图转换string，unsigned long，unsigned long long。

(1) set的测试

int main()
{
    std::bitset<4> foo;

	std::cout << foo.set() << '\n';       // 1111
	std::cout << foo.set(2, 0) << '\n';    // 1011
	std::cout << foo.set(2) << '\n';      // 1111

    return 0;
}
1
2
3
4
5
6
7
8
9
10

(2) reset的测试

int main()
{
    std::bitset<4> foo(std::string("1011"));

	std::cout << foo.reset(1) << '\n';    // 1001
	std::cout << foo.reset() << '\n';     // 0000
    return 0;
}
1
2
3
4
5
6
7
8

(3) flip的测试

int main()
{
  std::bitset<4> foo (std::string("0001"));

  std::cout << foo.flip(2) << '\n';     // 0101
  std::cout << foo.flip() << '\n';      // 1010

return 0;
}

1
2
3
4
5
6
7
8
9
10

运行结果：

---

3. 位图的模拟实现

    template<size_t N>
	class bitmap
	{
	private:
		std::vector<char> _bits;
	public:

		bitmap()
		{
			_bits.resize(N/8 +1, 0);
		}

		void set(size_t pos)
		{
			int i = pos / 8;
			int j = pos % 8;

			_bits[i] |= (1 << j);
		}

		void reset(size_t pos)
		{
			int i = pos / 8;
			int j = pos % 8;

			_bits[i] &= ~(1 << j);
		}

		bool test(size_t pos)
		{
			int i = pos / 8;
			int j = pos % 8;

			if (_bits[i] & (1 << j))
			{
				return true;
			}
			else
			{
				return false;
			}
		}
	};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

关于位图的模拟实现，我呢，只模拟实现三个函数接口分别是 set(),reset()和test()。这三个是比较关键的功能。

(1)构造函数

位图的底层是vector，我打算位图开辟空间，以char为单位开辟：

    template<size_t N>
	class bitmap
	{
	private:
		std::vector<char> _bits;
	public:
	    bitmap()
		{
			_bits.resize(N/8 +1, 0);
		}
	};
1
2
3
4
5
6
7
8
9
10
11

它的底层是vector< char >_bits，我要开辟N个比特位，怎么初始化？

直接resize(N) 肯定不可以，因为这是开辟N个char，我要的是开辟N个比特位。所以就是
resize(N/8) ;但是如果我要开辟6个比特位，N/8 == 0,这就导致开辟的空间为0，所以还不能直接是N/8，因为有可能要求开辟的比特位 < 8，所以简单粗暴些，直接开辟 N/8 +1 个char，这就解决问题了。

---

(2) set() ,unset(),test() 的实现

set()的实现：

        void set(size_t pos)
		{
			int i = pos / 8;
			int j = pos % 8;

			_bits[i] |= (1 << j);
		}
1
2
3
4
5
6
7

首先得找到 它的位置，怎么找？

int i = pos/8; 相当于找到了它在哪一个char中。
int j = pos%8;相当于找到了它要映射在char哪个位置上。

有点抽象，其实好理解，我画个图：

下面我开辟了 6个char的大小的位图，假如我要set的值是 10。

10/8 = 1，所以它要映射在 下标为 1的char中。

10 %8 =2，所以它将 下标为 1的char的第2个比特位设置为 1。

那么是怎么将某个位置，设置为 1的呢？

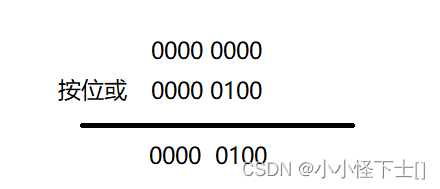
_bits[i] |= (1 << j); 将 1 左移 j 位 ，然后再按位或：
以上面为 例子：

---

reset()的实现：

        void reset(size_t pos)
		{
			int i = pos / 8;
			int j = pos % 8;

			_bits[i] &= ~(1 << j);
		}
1
2
3
4
5
6
7

还是先找到位置，然后再进行一个位运算：

比如原来的位图是 0000 0100 ，

传参 pos = 10，那么将 0000 0001 左移位 2 -> 0000 00100 ，然后再按位取反 -> 1111 1011

最后 和原来的位图 按位与，就可以使得 具体某个位置 由 1 置 0。

---

test()的实现:

        bool test(size_t pos)
		{
			int i = pos / 8;
			int j = pos % 8;

			if (_bits[i] & (1 << j))
			{
				return true;
			}
			else
			{
				return false;
			}
		}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

毫无疑问还是先找到映射的位置，然后 利用 位运算 来判断 映射位置是否为 1。

---

4. 位图的应用

4.1 给定100亿个整数，设计算法找到只出现一次的整数？

这里应该用位图：

我们来想一想思路，100亿个整数，找到只出现一次的整数，暴力的解法：可以利用计数排序，统计100亿整数中，所有数据出现的次数，找到只出现一次的整数。或者 可以利用 map来保存键值对<整数，出现次数>，也可以完成。但是 100亿的整数是不是有点大呀？一个整数占 4个字节，100亿的话，占40GB空间，所以显然不能暴力求解。

都说位图节省空间，来考虑用位图。100亿的整数 有几种情况？出现一次，出现两次及以上。就以上这么两种情况。我要的是找到只出现一次的整数。

俩种情况 几个比特位可以解决问题?

一个比特位： 0 表示不存在，1表示存在

额，一个比特位，不能解决问题，它无法表示数据出现了多次的情况。

俩个比特位：00 表示不存在；0 1 表示出现一次；1 0 表示出现两次以上

昂，看来俩个比特位就可以解决问题了，但是位图的映射 只是映射到一个比特位上，怎么办？搞出来俩个位图就可以了，对吧？

代码实现：

    template <size_t N>
	class two_bitset
	{
	private:
		bitmap<N> _bits1;
		bitmap<N> _bits2;

	public:
		void two_set(size_t pos)
		{
			if (!_bits1.test(pos) && !_bits2.test(pos))
			{    
				// 原本是 00 ，出现一次设置为 0 1
				_bits2.set(pos);
			}
			else if (!_bits1.test(pos) && _bits2.test(pos))
			{    
				// 出现了一次，那么再次出现，那就 设置 为 1 0
				_bits2.reset(pos);
				_bits1.set(pos);
			}

			else
			{
				/// 俩次以上，不需要处理
			}   
		}

		void two_test()
		{
			for (size_t i = 0; i < N; i++)
			{
				if (!_bits1.test(i) && _bits2.test(i))
				{
					std::cout << i << std::endl;
				}
			}
		}
	};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

4.2 给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

俩个文件分别有100亿个整数，这次不需要求只出现一次的数字，但是要求我们找到它们的交集。

毫无疑问还是位图，怎么操作？首先我们得明白如何用位图去求交集。

举例：俩个位图按位与一下，就能够求出位图的交集。

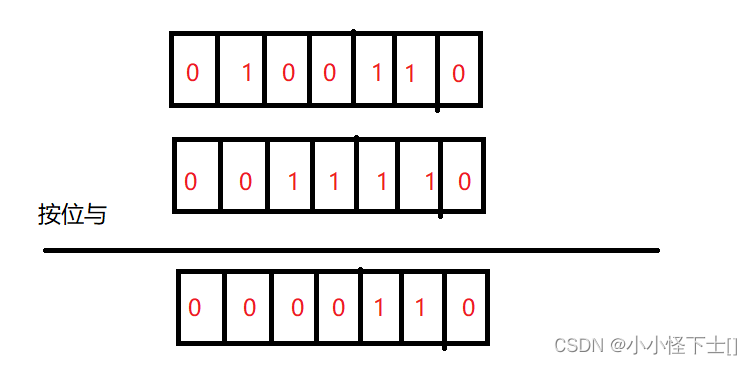
有了这个思路，就好办多了，我们得有三个位图。

前两个位图 分别 去插入 100亿整数，其实每个位图 也就占 500Mb空间，相比 要开辟40GB节省了很多空间。

最后一个位图，保存 前俩个位图 ，按位与后的结果，那么这个位图保存的就是 交集。

代码实现思路，注意是思路哈：

bitset<N> _bits1;
bitset<N> _bits2;
bitset<N> _bitans;

for(auto i : file1)
{
  _bits1.set(i);
}
for(auto i : file2)
{
  _bits2.set(i);
}

for(size_t n =0;n<N;i++)
{
    if(_bits1.test(n)&&_bits2.test(n))
    _bitans.set(n);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

---

4.3 位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数

这其实就是第一题的变形，它要求找到出现次数不超过2次的整数。

那还是 两个位图：

00 表示 没有出现
01 表示 出现一次
10 表示 出现两次
11 表示 出现三次以上

嗯，就是这样，很简单的，对吧？

    template <size_t N>
	class two_bitset
	{
	private:
		bitmap<N> _bits1;
		bitmap<N> _bits2;

	public:
		void two_set(size_t pos)
		{
			if (!_bits1.test(pos) && !_bits2.test(pos))
			{    
				// 原本是 00 ，出现一次设置为 0 1
				_bits2.set(pos);
			}
			else if (!_bits1.test(pos) && _bits2.test(pos))
			{    
				// 出现了一次，那么再次出现，那就 设置 为 1 0
				_bits2.reset(pos);
				_bits1.set(pos);
			}

			else if (_bits1.test(pos) && !_bits2.test(pos))
			{
			     // 原本是出现两次，这是第三次
				_bits2.set(pos);
			}
			else
			{
			    // 三次及以上 不做处理
			}   
		}

		void two_test()
		{
			for (size_t i = 0; i < N; i++)
			{
				if ((!_bits1.test(i) && _bits2.test(i))||(_bits1.test(i) && !_bits2.test(i)))
				{
					std::cout << i << std::endl;
				}
			}
		}
	};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

---