深度学习基础之《TensorFlow框架（15）—神经网络》

一、神经网络基础

1、什么是神经网络
人工神经网络（Artificial Neural Network，简写为ANN）。也简称为神经网络（NN）
是一种模仿生物神经网络（动物的中枢神经系统，特别是大脑）结构和功能的计算模型
经典的神经网络结构包含三个层次的神经网络。分别为输入层、输出层以及隐藏层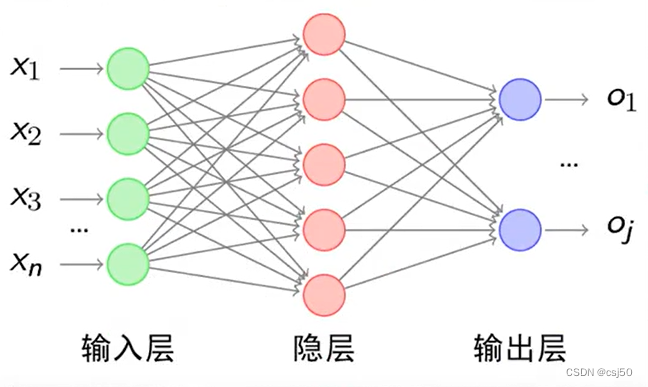

其中每层的圆圈代表一个神经元，隐藏层和输出层的神经元有输入的数据计算后输出，输入层的神经元只是输入

2、神经网络的特点
（1）每个连接都有个权值
（2）同一层神经元之间没有连接
（3）最后的输出结果对应的层也称之为全连接层
神经网络是深度学习的重要算法，在图像（如图像的分类、检测）和自然语言处理（如文本分类、聊天等）有很多应用

3、为什么设计这样的结构呢
首先从一个最基础的结构说起—神经元。以前也称之为感知机。神经元就是要模拟人的神经元结构
一个神经元通常具有多个树突，主要用来接受传入信息。而轴突只有一条，轴突尾端有许多轴突末梢可以给其他多个神经元传递信息。轴突末梢跟其他神经元的树突产生连接，从而传递信号。这个连接的位置在生物学上叫“突触”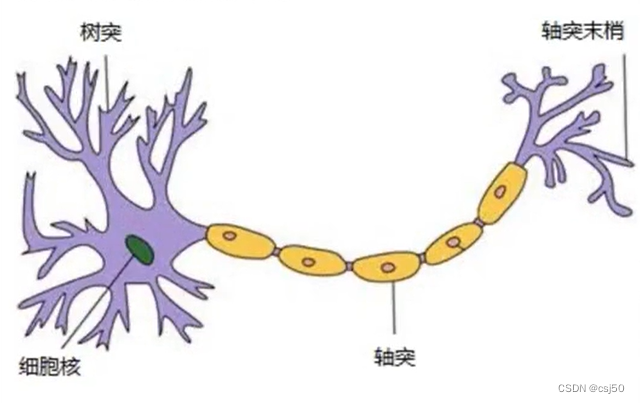

4、感知机
PLA：Perceptron Learning Algorithm
感知机就是模拟这样的大脑神经网络处理数据的过程。感知机模型如下：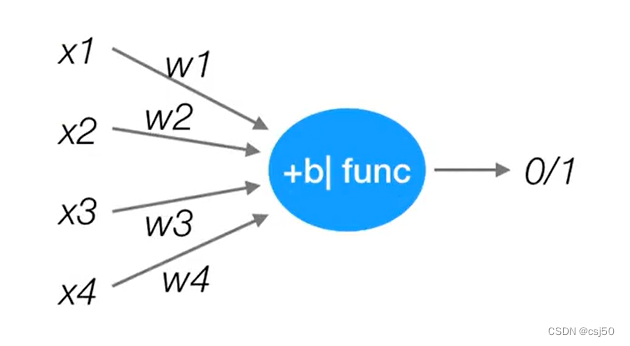

感知机是一种基础的分类模型，类似于逻辑回归，不同的是，感知机的激活函数用的是sign，而逻辑回归用的sigmoid。感知机也具有连接的权重和偏置
输入层有x1 x2 x3 x4四个特征，相当于树突收集信息，每个树突都带有权重，加权，加权之后结果再经过偏置，一系列的处理，再经过激活函数func，最后输出

u=加权(权重*特征值)+偏置
u映射到sign(u)函数当中，如果u大于0，就给正1，如果u小于等于0，就给负1

sign函数：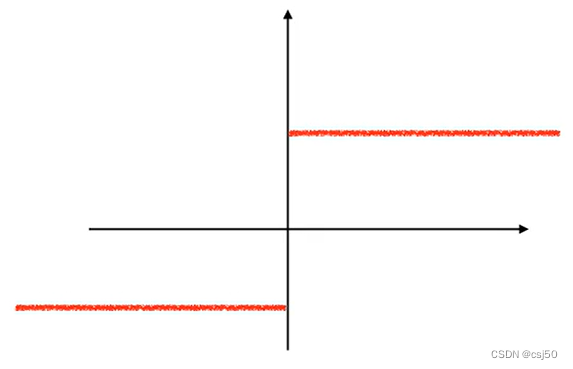

5、感知机可以解决的问题 — 简单的或、与问题
或问题：
x1 x2
0  0 => 0
0  1 => 1
1  0 => 0
1  1 => 1
与问题：
x1 x2
0  0 => 0
0  1 => 0
1  0 => 0
1  1 => 1

相当于用w1x1 + w2x2，看和阈值b之间的关系

二、playground使用

1、网址https://playground.tensorflow.org/

2、playground演示
目标：区分红点和蓝点
FEATURES：是特征
HIDDEN LAYER：是隐藏层
neurons：是神经元

（1）特征只按照直线分割，2个神经元，没有激活函数
计算不出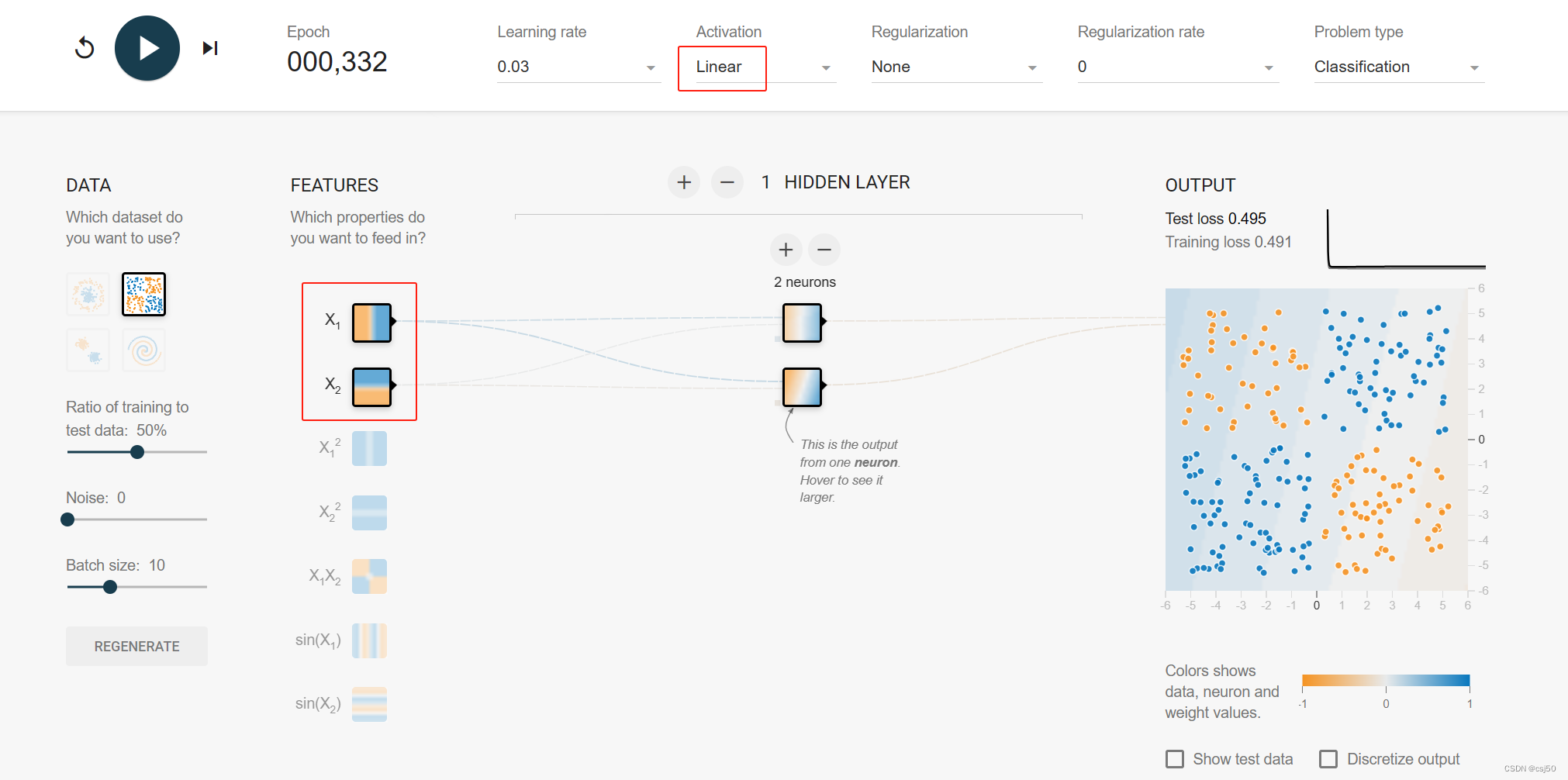

（2）特征只按照直线分割，加了两层，各4个神经元，设置激活函数
基本可以计算出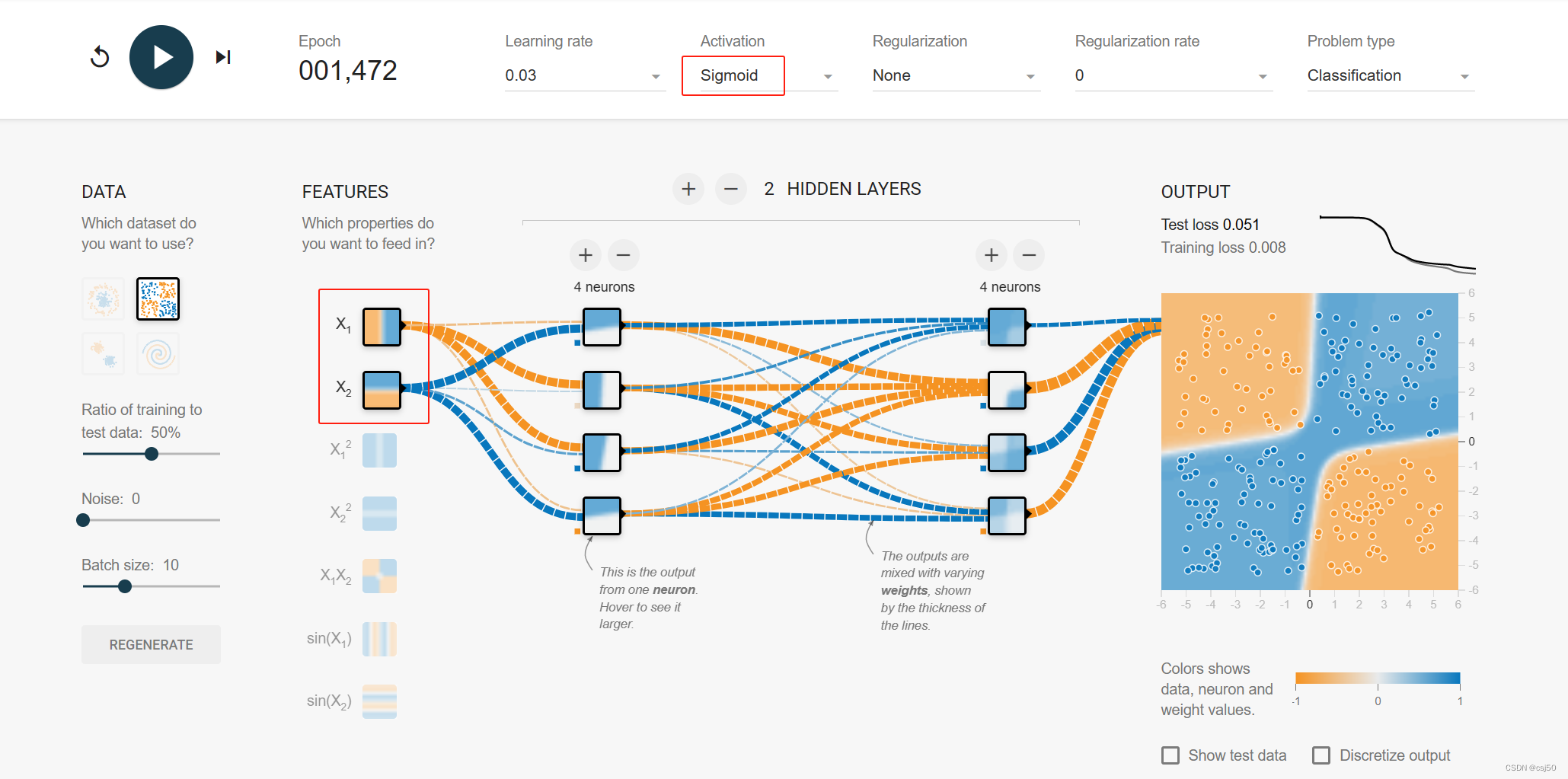

（3）特征按照十字分割，2个神经元，没有激活函数
可以计算出来

可以看出特征取的准确，很快可以计算出来。特征取的不是那么完整，可以通过增加神经元和激活函数计算出来

三、神经网络原理

1、神经网络的主要用途在于分类，那么整个神经网络分类的原理是怎么样的？
围绕损失、优化这两块内容

2、神经网络输出结果如何分类？
神经网络解决多分类问题最常用的方法是设置n个输出节点，其中n为类别的个数
任意事件发生的概率都在0和1之间，且总有某一个事件发生（概率的和为1）。如果将分类问题中“一个样例属于某一个类别”看成一个概率事件，那么训练数据的正确答案就符合一个概率分布。如何将神经网络前向传播得到的结果也变成概率分布呢？softmax回归就是一个非常常用的方法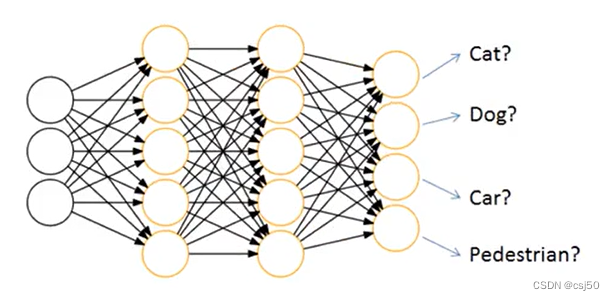

四、softmax回归

1、softmax回归将神经网络输出转换成概率结果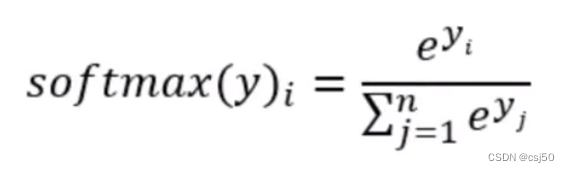

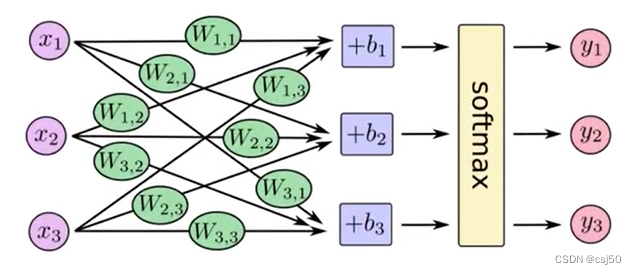
前面是线性回归的输出，如果是二分类问题，加上sigmoid。如果是多分类问题，加上softmax

2、如何理解这个公式的作用呢？
计算案例：
假设softmax之前输出结果为：2.3，4.1，5.6
softmax的计算输出结果为：
y1_p = e^2.3 / (e^2.3 + e^4.1 + e^5.6) = 0.02927204546
y1_p = e^4.1 / (e^2.3 + e^4.1 + e^5.6) = 0.17708555558
y1_p = e^5.6 / (e^2.3 + e^4.1 + e^5.6) = 0.79364239896

这样就把神经网络的输出也变成了一个概率输出
0.02927204546 + 0.17708555558 + 0.79364239896，三个值加在一起等于1

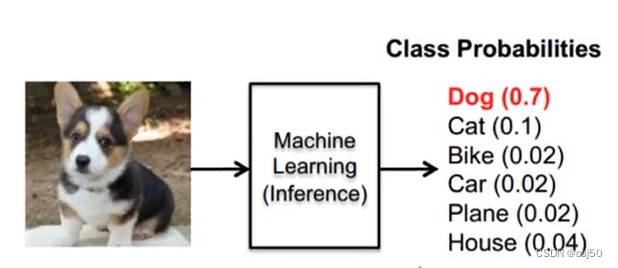
3、这个函数类似于逻辑回归当中的sigmoid函数，sigmoid输出的是某个类别的概率

4、想一想线性回归的损失函数以及逻辑回归的损失函数，那么如何去衡量神经网络预测的概率分布和真实答案的概率分布的距离？

线性回归损失函数：最小二乘法、均方误差
逻辑回归损失函数：对数似然函数

五、损失函数—交叉熵损失

1、公式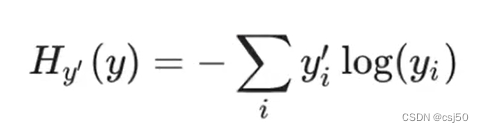

（yi是预测概率，yi撇是真实值）为了能够衡量距离，目标值需要进行one-hot编码，能与概率值一一对应：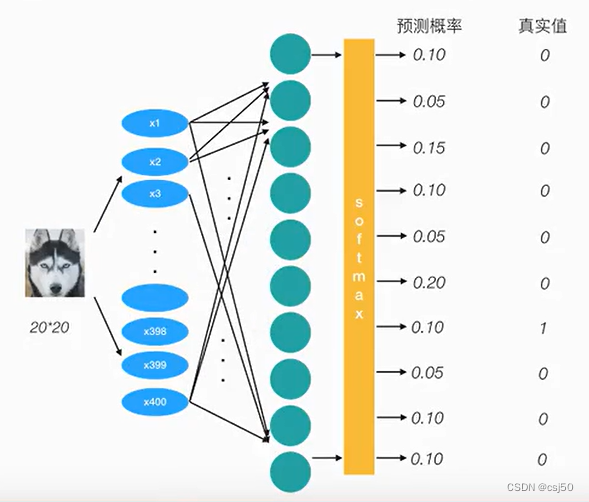

2、损失如何进行计算
样本是20x20的图片，所以有400个特征，经过计算输出logits。logits经过softmax映射，出来预测概率值
-(0*log(0.10)+0*log(0.05)+...+1*log(0.10)+0*log(0.05)+0*log(0.10)+0*log(0.10))
结果为-1*log(0.10)

优化损失，为了减少这一个样本的损失，神经网络应该怎么做？
所以会提高对应目标值为1的位置输出概率大小，由于softmax公式影响，其他的概率必定会减少。只要进行这样的调整就可以预测成功了！！！

3、损失大小
神经网络最后的损失为平均每个样本的损失大小
对所有样本的损失求和取其平均值

4、训练
训练过程中计算机会尝试一点点增大或减小每个参数，看其能如何减少相比于训练数据集的误差，以望能找到最优的权重、偏置参数组合

六、softmax、交叉熵损失API

1、tf.nn.softmax_cross_entropy_with_logits(labels, logits, name=None)
说明：
（1）计算logits和labels之间的交叉损失熵
（2）labels：标签值（真实值）
（3）logits：样本加权之后的值
（4）return：返回损失值列表

2、tf.reduce_mean(input_tensor)
计算平均值