- 1GitHub版Devin上线,会打字就能开发应用,微软CEO:重新定义IDE
- 2git did not exit cleanly (exit code 128)_git did not cleanly code128
- 3WPF之textbox输入框
- 4线性代数的学习和整理11: 子式与余子式_代数余子式
- 5后端开发常见问题_后端项目开发中遇到的问题
- 6Azure File- 一种从本地同步到云的 文件共享方式_java azure file storage 实现微软云上传下载
- 7跨语种「AI同传」颠覆语音翻译!Meta谷歌连发重大突破_meta 语音翻译
- 8机器人博展中心_重磅!2020RoboCom(睿抗)机器人大赛全国总决赛正式拉开帷幕!...
- 9Coze.cn - 编织AI未来的在线平台
- 10AI:165-Coze自定义赛博风格Bot-图片生成操作指南
【查找算法】顺序、二分、索引、哈希_二分法查找和顺序查找
赞
踩
目录
1. 顺序查找
- 从表中指定位置(一般为最后一个,第0个位置设为岗哨)的记录开始,沿某个方向将记录的关键字与给定值相比较若某个记录的关键字和给定值相等,则查找成功;
- 反之,若找完整个顺序表,都没有与给定关键字值相等的记录,则此顺序表中没有满足查找条件的记录,查找失败。
1.1 性能分析
空间复杂度:O(1)
时间复杂度:最好O(1) 最坏O(n) 平均O(n)
1.2 平均查找长度

2. 二分查找
有序数组中不存在重复元素,用二分查找值等于给定值的数据。
- public int bsearch(int[] a, int n, int value) {
- int low = 0;
- int high = n - 1;
-
- while (low <= high) {
- int mid = (low + high) / 2;
- if (a[mid] == value) {
- return mid;
- } else if (a[mid] < value) {
- low = mid + 1;
- } else {
- high = mid - 1;
- }
- }
-
- return -1;
- }

- // 二分查找的递归实现
- public int bsearch(int[] a, int n, int val) {
- return bsearchInternally(a, 0, n - 1, val);
- }
-
- private int bsearchInternally(int[] a, int low, int high, int value) {
- if (low > high) return -1;
-
- int mid = low + ((high - low) >> 1);
- if (a[mid] == value) {
- return mid;
- } else if (a[mid] < value) {
- return bsearchInternally(a, mid+1, high, value);
- } else {
- return bsearchInternally(a, low, mid-1, value);
- }
- }

2.1 变体1:查找第一个值等于给定值的元素
比如一个数组a[10],其中的a[5],a[6],a[7]都为8,需要找到第一个等于8的a[5]需要怎么办呢?
- public int bsearch(int[] a, int n, int value) {
- int low = 0;
- int high = n - 1;
- while (low <= high) {
- int mid = low + ((high - low) >> 1);
- if (a[mid] > value) {
- high = mid - 1;
- } else if (a[mid] < value) {
- low = mid + 1;
- } else {
- if ((mid == 0) || (a[mid - 1] != value)) return mid; //*1
- else high = mid - 1; //*2
- }
- }
- return -1;
- }

a[mid] 与 value的关系有三种情况:
- a[mid] > value; high = mid - 1;
- a[mid] < value; low = mid + 1;
- a[mid] = value; 此时需要判断a[mid]是不是第一个值等于给定值的元素。
看标注*的两行:
如果mid等于0,那这个元素已经是数组的第一个元素,那它肯定是我们要找的;如果mid不等于0,但a[mid]的前一个元素a[mid-1]不等于value,那也说明a[mid]就是我们要找的第一个值等于给定值的元素。
如果经过检查之后发现a[mid]前面的一个元素a[mid-1]也等于value,那说明此时的a[mid]肯定不是我们要查找的第一个值等于给定值的元素。那我们就更新high=mid-1,因为要找的元素肯定出现在[low, mid-1]之间。
2.2 变体2:查找最后一个值等于给定值的元素
根据上一种情况进行修改即可。
- public int bsearch(int[] a, int n, int value) {
- int low = 0;
- int high = n - 1;
- while (low <= high) {
- int mid = low + ((high - low) >> 1);
- if (a[mid] > value) {
- high = mid - 1;
- } else if (a[mid] < value) {
- low = mid + 1;
- } else {
- if ((mid == n-1) || (a[mid + 1] != value)) return mid; //*1
- else low = mid + 1; //*2
- }
- }
- return -1;
- }

如果a[mid]这个元素已经是数组中的最后一个元素了,那它肯定是我们要找的;如果a[mid]的后一个元素a[mid+1]不等于value,那也说明a[mid]就是我们要找的最后一个值等于给定值的元素。
如果我们经过检查之后,发现a[mid]后面的一个元素a[mid+1]也等于value,那说明当前的这个a[mid]并不是最后一个值等于给定值的元素。我们就更新low=mid+1,因为要找的元素肯定出现在[mid+1, high]之间。
2.3 变体3:查找第一个大于等于给定值的元素
在有序数组中,查找第一个大于等于给定值的元素。比如,数组中存储的这样一个序列:3,4,6,7,10。如果查找第一个大于等于5的元素,那就是6。
- public int bsearch(int[] a, int n, int value) {
- int low = 0;
- int high = n - 1;
- while (low <= high) {
- int mid = low + ((high - low) >> 1);
- if (a[mid] >= value) {
- if ((mid == 0) || (a[mid - 1] < value)) return mid;
- else high = mid - 1;
- } else {
- low = mid + 1;
- }
- }
- return -1;
- }
如果a[mid]小于要查找的值value,那要查找的值肯定在[mid+1, high]之间,所以,我们更新low=mid+1。
对于a[mid]大于等于给定值value的情况,我们要先看下这个a[mid]是不是我们要找的第一个值大于等于给定值的元素。如果a[mid]前面已经没有元素,或者前面一个元素小于要查找的值value,那a[mid]就是我们要找的元素。这段逻辑对应的代码是第7行。
如果a[mid-1]也大于等于要查找的值value,那说明要查找的元素在[low, mid-1]之间,所以,我们将high更新为mid-1。
2.4 变体4: 查找最后一个小于等于给定值的元素
比如,数组中存储了这样一组数据:3,5,6,8,9,10。最后一个小于等于7的元素就是6。是不是有点类似上面那一种?实际上,实现思路也是一样的。
- public int bsearch7(int[] a, int n, int value) {
- int low = 0;
- int high = n - 1;
- while (low <= high) {
- int mid = low + ((high - low) >> 1);
- if (a[mid] > value) {
- high = mid - 1;
- } else {
- if ((mid == n - 1) || (a[mid + 1] > value)) return mid;
- else low = mid + 1;
- }
- }
- return -1;
- }
3. 索引查找
大量的无序数组
- 先分析数据规律,建立索引
- 再根据索引进行快速定位
- 在定位的地方进行细致搜索
3.1 索引表的构建

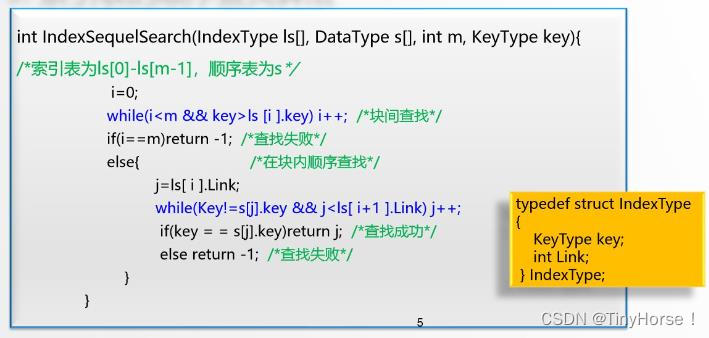
3.2 索引表的查找
索引表是有序的,查找可以用顺序查找 或 二分查找
块内如果有序可以用顺序查找 或 二分查找,块内如果无序则用顺序查找
块内查找如何结束
- 如果找到了,查找成功,结束;
- 如果已经查找到下一个块了,则证明查找失败;
- 对于最后一个块要增加一个索引项n+1,如果查找最后一个块时已经到了n+1位置,则证明查找失败。
3.3 索引顺序查找的ASL
ASL=ASL(索引表)+ASL(块内)
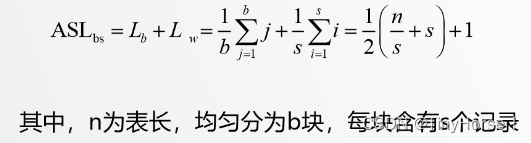
4. 三种查找方法比较

5. 哈希查找
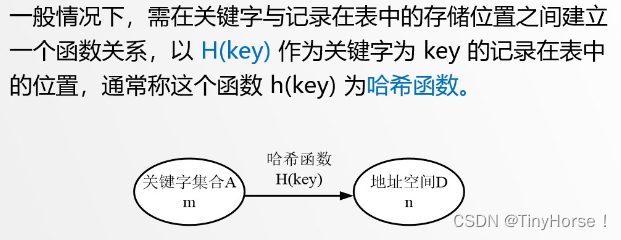
5.1 哈希函数
5.2 哈希表
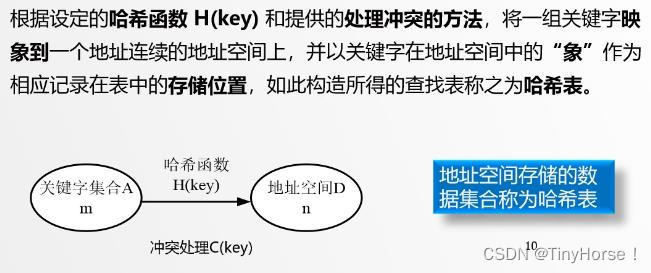
5.3 哈希函数构造方法
5.3.1 直接定址法
取关键字或关键字的某个线性函数值为哈希地址。即:
H(key)=key 或 H(key)=a*key+b
5.3.2 数字分析法
假设关键字是以r为基的数(如:以10为基的十进制数),并且哈希表中可能出现的关键字都是事先知道的,则可取关键字的若干数位组成哈希地址。

5.3.3 平方取中法
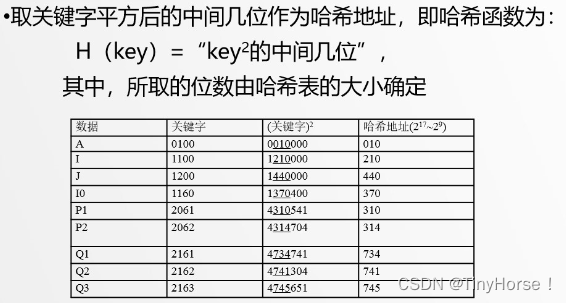
5.3.4 折叠法

5.3.5 除留余数法

5.3.6 随机数法



