对偶锥

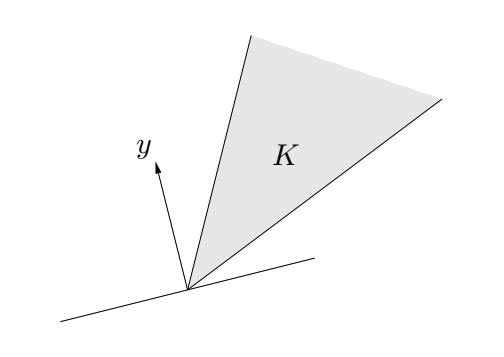
若 $K$ 为一个锥，那么它的对偶锥的定义为：
K∗={y∣x⋅y≥0 for all x∈K}K^\ast=\{y\mid x\cdot y\geq 0 \text{ for all } x\in K\}K∗={y∣x⋅y≥0 for all x∈K}

上式中的点表示内积。（两个矩阵的内积等于他们乘积的迹）

在几何意义上，对偶锥上的一条线 $y$ 一定属于 $K$ 其中一个支撑超平面的法线。例如下图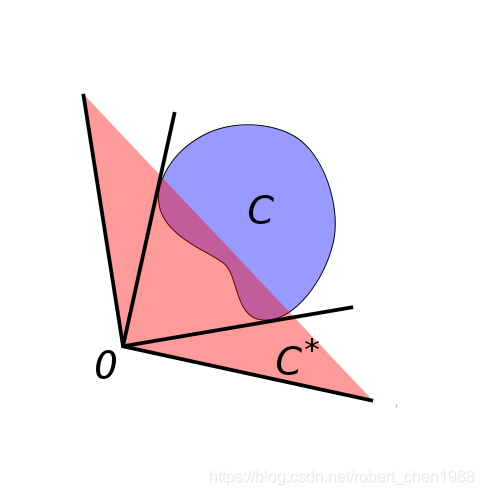


上图中的红色区域就是 $C$ 的对偶锥。

几个实例

• 子空间（线性子空间） $V$ 的对偶锥是它的正交补.
  V∗=V⊥={y∣yTv=0}V^\ast=V^{\perp}=\{y\mid y^Tv=0\}V∗=V⊥={y∣yTv=0}
  利用了一个性质：若 $x\in V$，则 $-x\in V$.
• 非负象限的对偶锥是它自身.
• 半正定矩阵的对偶锥是它自身.
• 范式锥的对偶锥是它的对偶范式锥.