数据结构【1】【简单排序】冒泡、选择、插入原理、实现、时间复杂度分析_简述插入选择冒泡排序实现原理

1. 比较相邻的元素。如果前一个元素比后一个元素大，就交换这两个元素的位置。

2. 对每一对相邻元素做同样的工作，从开始第一对元素到结尾的最后一对元素。最终最后位置的元素就是最大

完整代码：

public class Bubble {
    //对数组a中的元素进行排序
    public static void sort(Comparable[] a) {
        for (int i=a.length-1;i>0;i--) {
            for(int j=0;j<i;j++){
                //比较索引j和j+1处的值
                if(greater(a[j],a[j+1])){
                    exch(a,j,j+1);
                }
            }
        }
    }
 
    //比较v元素是否大于w元素
    public static boolean greater(Comparable v, Comparable w) {
        return v.compareTo(w) > 0;
    }
 
    //数组元素交换位置
    private static void exch(Comparable[] a, int i, int j) {
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
 
}

sort(Comparable a[]){
    for(int i = a.length()-1;i>0;i--){
        for(int j=0;i<i;j++){
            if(greater(a[j],a[j+1])){
                exchange(a[j],a[j+1]);
            }
        }
    }
}

1.2.2冒泡排序的时间复杂度

比较次数 = 交换次数

O(N^2)

1.3选择排序

1.3.1代码及原理实现

 1.每一次遍历的过程中，都假定第一个索引处的元素是最小值，和其他索引处的值依次进行比较，如果当前索引处的值大于其他某个索引处的值，则假定其他某个索引出的值为最小值，最后可以找到最小值所在的索引
 2.交换第一个索引处和最小值所在的索引处的值

逻辑图

 完整代码

public class Selection {
    //对数组a中元素进行排序
    public static void sort(Comparable[] a){
        for (int i = 0; i <=a.length-2 ; i++) {
            //定义一个变量，定义最小元素所在的索引，默认参与选择排序的第一个元素所在的位置
            int minIndex = i;
            for (int j = i+1; j < a.length; j++) {
                //比较最小索引处minIndex处的值和j索引处的值
                if(greater(a[minIndex],a[j]))
                {
                    minIndex=j;
                }
            }
            exch(a,i,minIndex);
        }
    }
 
    //比较v元素是否大于w元素
    public static boolean greater(Comparable v, Comparable w) {
        return v.compareTo(w) > 0;
    }
 
    //数组元素交换位置
    private static void exch(Comparable[] a, int i, int j) {
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

核心代码：

    public static void sort(Comparable[] a){
        for (int i = 0; i <=a.length-2 ; i++) {//最后两个数不用比较
            //定义一个变量，定义最小元素所在的索引，默认参与选择排序的第一个元素所在的位置
            int minIndex = i;
            for (int j = i+1; j < a.length; j++) {
                //比较最小索引处minIndex处的值和j索引处的值
                if(greater(a[minIndex],a[j]))
                {
                    minIndex=j;
                }
            }
            exch(a,i,minIndex);
        }
    }

1.3.2时间复杂度分析：

选择排序使用了双层for循环，其中外层循环完成了数据交换，内层循环完成了数据比较，所以分别统计数据交换次数

和数据比较次数：

数据比较次数： (N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2;

数据交换次数： N-1

总计：N^2/2-N/2+(N-1)=N^2/2+N/2-1;

根据大O推导法则，保留最高阶项，去除常数因子，时间复杂度为O(N^2);

1.4插入排序

1.4.1插入排序原理及代码实现

原理：

1.把所有的元素分为两组，已经排序的和未排序的；

2.找到未排序的组中的第一个元素，向已经排序的组中进行插入；

3.倒叙遍历已经排序的元素，依次和待插入的元素进行比较，直到找到一个元素小于等于待插入元素，那么就把待 插入元素放到这个位置，其他的元素向后移动一位；

API设计

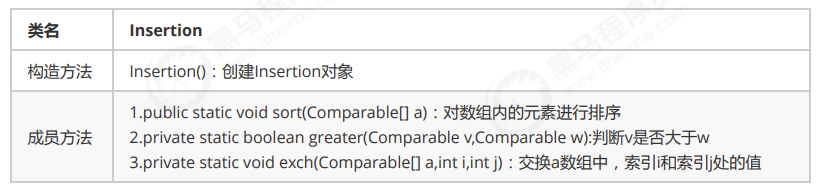
完整代码：

package sort;
 
public class Insertion {
    public static void sort(Comparable[] a){
        for (int i = 1; i < a.length; i++) {
            for (int j = i; j > 0 ; j--) {
                //比较索引j处的值和索引j-1处的值，如果索引j-1处的值比索引j处的值大，则交换数据，如果不大，那么就找到合适的位置了，退出循环即可；
                if (greater(a[j-1],a[j])){
                    exch(a,j-1,j);
                }else{
                    break;
                }
            }
        }
    }
 
 
    //比较v元素是否大于w元素
    public static boolean greater(Comparable v, Comparable w) {
        return v.compareTo(w) > 0;
    }
 
    //数组元素交换位置
    private static void exch(Comparable[] a, int i, int j) {
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

核心代码：

    public static void sort(Comparable[] a){
        for (int i = 1; i < a.length; i++) {
            for (int j = i; j > 0 ; j--) {
                //比较索引j处的值和索引j-1处的值，如果索引j-1处的值比索引j处的值大，则交换数据，如果不大，那么就找到合适的位置了，退出循环即可；
                if (greater(a[j-1],a[j])){
                    exch(a,j-1,j);
                }else{
                    break;
                }
            }
        }
    }

插入排序使用了双层for循环，其中内层循环的循环体是真正完成排序的代码，所以，我们分析插入排序的时间复 杂度，主要分析一下内层循环体的执行次数即可。

最坏情况，也就是待排序的数组元素为{12,10,6,5,4,3,2,1}，那么：

比较的次数为： (N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2;

交换的次数为： (N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2;

总执行次数为： (N^2/2-N/2)+(N^2/2-N/2)=N^2-N;

按照大O推导法则，保留函数中的最高阶项那么最终插入排序的时间复杂度为O(N^2).

1.5其他参考篇章

详解参考文章——视频 | 手撕九大经典排序算法，看我就够了！