2021年蓝桥杯赛题【Python】_蓝桥杯python

【填空】

1、卡片

小蓝有很多数字卡片，每张卡片上都是数字 0 到 9。 小蓝准备用这些卡片来拼一些数，他想从 1 开始拼出正整数，每拼一个， 就保存起来，卡片就不能用来拼其它数了。 小蓝想知道自己能从 1 拼到多少。
例如，当小蓝有 30 张卡片，其中 0 到 9 各 3 张，则小蓝可以拼出 11 到 1010， 但是拼 11 时卡片 1 已经只有一张了，不够拼出 11。
现在小蓝手里有 0 到 9 的卡片各 2021 张，共 20210张，请问小蓝可以从 1 拼到多少？

import os
import sys
n = sys.maxsize
num = 0
for i in range(1,n):
    num += str(i).count('1')
    if num > 2021:
      print(i-1)
      break
#结果：3181
1
2
3
4
5
6
7
8
9
10

2、空间

请问 256MB 的空间可以存储多少个 32 位二进制整数？

#需要知道32位二进制占内存4B
n = 256*1024*1024
print(int(n/4))
1
2
3

3、路径

问题描述

小蓝学习了最短路径之后特别高兴，他定义了一个特别的图，希望找到图 中的最短路径。
小蓝的图由 2021 个结点组成，依次编号 1 至 2021。
对于两个不同的结点 a, b，如果 a 和 b 的差的绝对值大于 21，则两个结点 之间没有边相连；如果 a 和 b 的差的绝对值小于等于 21，则两个点之间有一条 长度为 a 和 b 的最小公倍数的无向边相连。
例如：结点 1 和结点 23 之间没有边相连；结点 3 和结点 24 之间有一条无 向边，长度为 24；结点 15 和结点 25 之间有一条无向边，长度为 75。

计算要求
请计算，结点 1 和结点 2021 之间的最短路径长度是多少。

思路
1、算法：dp动态规划
2、步骤

• 构造一个n*n的矩阵
• 利用两个for循环，遍历1到2021的最短路径，每次遍历数时，对应的数值会变化成最短路径
• 到最后，索引值为2021，便是最优路径

3、将1到2021路径最短问题->n个类似与1到（2,22）的最短路径的小问题。

import math
#求最大公因数
# def gcd(a,b):
#   if b == 0:
#     return a
#   else:
#     return gcd(b,a%b)
#求最小公倍数
# def gbs(a,b):
#   return a*b // gcd(a,b)
dp = [float('inf')] * (2021+1) #inf正无穷
dp[1] = 0
for i in range(1,2022):
  for j in range(i+2,i+22):
    if j > 2021:
      break
    # dp[j] = min(dp[j] , dp[i]+gbs(i,j))
    dp[j] = min(dp[j] , dp[i]+i*j // math.gcd(i,j))

print(dp[2021])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

4、相乘

问题描述

小蓝想知道，能不能在 1 至 1000000007 之间找到一个数，与 2021 相乘后 再除以 1000000007后的余数为 999999999。

结果提交
如果存在，请在答案中提交这个数； 如果不存在，请在答案中提交 0。

分析

1. 不能直接依据题目那样所讲的遍历1~1000000007，不然会超时
2. 转换下运算公式

#超时
# for i in range(1,1000000008):
#   n = (i*2021) % 1000000007
#   if n == 999999999:
#     print(i)
#     break

for i in range(1,2022):
  if (i*1000000007+999999999) % 2021 == 0:
    print(int((i*1000000007+999999999) / 2021))
    break 
1
2
3
4
5
6
7
8
9
10
11

5、回路计数

6、距离和

问题描述
两个字母之间的距离定义为它们在字母表中位置的距离。例如 AA 和 CC 的距离为 22，LL 和 QQ 的距离为 55。
对于一个字符串，我们称字符串中两两字符之间的距离之和为字符串的内部距离。
例如：ZOO 的内部距离为 2222，其中 ZZ 和 OO 的距离为 1111。

求解
请问，LANQIAO 的内部距离是多少？

lst = 'LANQIAO'
# a = []
count = 0
n = len(lst)

#先转ASCLL码值，再相减，ord()转ascll值，abs（）绝对值
for i in range(n):
  for j in range(i+1,n):
    count += abs(ord(lst[i]) - ord(lst[j]))
print(count)
1
2
3
4
5
6
7
8
9
10

7、序列个数

请问有多少个序列满足下面的条件：
序列的长度为 5。
序列中的每个数都是 1 到 10 之间的整数。
序列中后面的数大于等于前面的数。

num=0
for i in range(10):
  for j in range(i,10):
    for m in range(j,10):
      for n in range(m,10):
        for k in range(n,10):
          num +=1
print(num)
1
2
3
4
5
6
7
8

8、数学位数

问题描述

整数 11 到 1212 连在一起，成为 123456789101112，长度为 1515。

求解
请问整数 11 到 20202020 连在一起，长度为多少？

import os
import sys
a = []
for i in range(1,2021):
  a.append(i)
ls = int("".join(map(str,a)))
num = len(str(ls))
print(num)
1
2
3
4
5
6
7
8

9、货物摆放

问题描述

import os
import sys

# 请在此输入您的代码
n = 2021041820210418 #货物数量 
count = 0 #统计值赋初始值0 
docker = set() #创建集合属性的容器

for i in range(1,int(n**0.5)+1): #循环遍历，筛选n的约数（对n开根号的写法能加快速度） 
    if n%i == 0: #判断约数 
      docker.add(i) #添加约数 
      docker.add(n//i)

for i in docker: #三重循环遍历容器（三重循环快到运行5秒出结果） 
    for j in docker: 
          for k in docker: 
            if i*j*k == n: 
              count += 1 #满足条件，方案数+1 
print(count) #打印结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

【设计题】

1、杨辉三角

问题描述


参考大佬博客

#阶乘
def C(a,b):
  i,j = a,1
  res = 1
  while j <= b:
    res = res*i/j
    i -= 1
    j += 1
  # print(res)
  return int(res)

#查找
def searve(x,n):
  minl  = 2*x  #下限 
  uppl = n #底数的最大上限C（4,2） and C(6,1)

  while minl <= uppl:
    mid = (uppl + minl) // 2
    if C(mid,x) == n:#取中
      print(int(mid* ( mid+1 ) /2 ) + x + 1)
      return True

    elif C(mid,x) > n: #数值大于所求的数，缩小上限范围
      uppl = mid - 1
    else:
      minl = mid + 1
  return False

n = int(input())

for i in range(16,-1,-1):
  if searve(i,n):#传送数的列位置和需要求的数值
    break
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

2、最小砝码

参考资料
问题描述

import os
import sys

N = int(input())
i = 1
ans = 1
while i<N:
  i = i*3 +1
  print(i)
  ans += 1
print(ans)
1
2
3
4
5
6
7
8
9
10
11

3、左孩子右兄弟

问题描述

考点

• 树结构
• 深度搜索DFS，每次探索一个节点到底，回去原点，再去其他的。
• 递归算法

个人解题思路
看图（比较潦草）

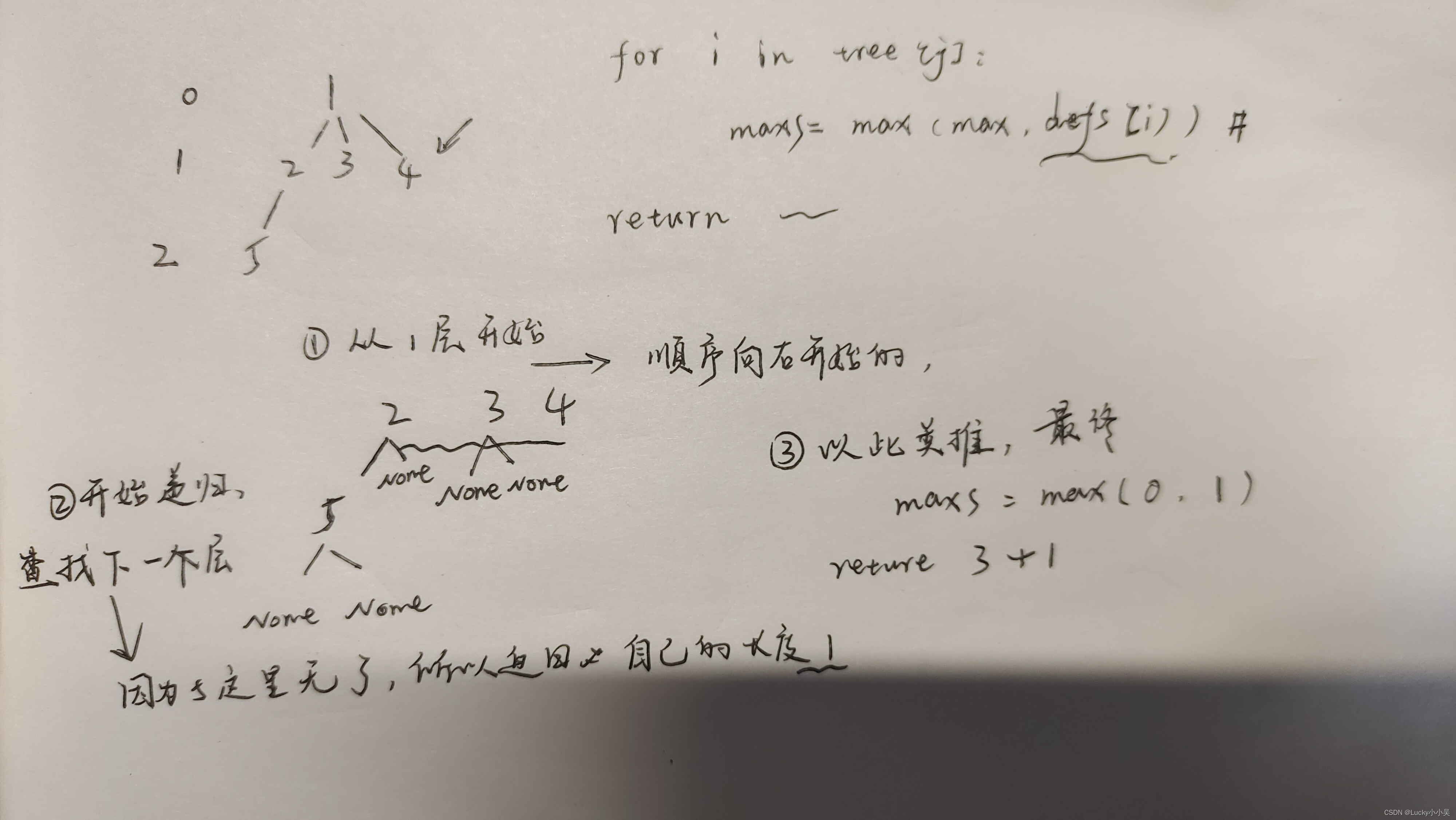
参考博客
左孩子右兄弟含义

import os
import sys

n = int(input())
#在这里，对于所有评测用例： 1000001≤N≤100000会出现递归次数频繁，导致无效返回
#原因：python默认的递归深度是很有限的，大约900多
sys.setrecursionlimit(1000000) 
tree = [[] for _ in range(n+1)]

#构造一个类似于树结构的二维列表
#例如题目中的1 1 1 2
"""
0 【1】
1 【2，3，4】
2 【5】
"""
for i in range(2,n+1):
    m = int(input())
    tree[m].append(i)

#深度搜索操作
def dfs(j):
  if tree[j] == None:
    return 0

  maxs = 0

  for i in tree[j]:
    maxs = max(maxs ,dfs(i)) #递归下一层数值，并返回其长度
  return len(tree[j])+maxs
print(dfs(1))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31