矩阵分解ALS-交替最小二乘法

ALS（alternating least squares）

ALS是交替最小二乘的简称。在机器学习中，ALS特指使用交替最小二乘求解的一个协同推荐算法。如：将用户（user）对商品（item）的评分矩阵分解成2个矩阵：

把原来的矩阵拆分成：

如何从评分矩阵中分解出User矩阵和Item矩阵，

• 只有左侧的评分矩阵R是已知的
• User矩阵和Item矩阵是未知
• 学习出User矩阵和Item矩阵，使得User矩阵*Item矩阵与评分矩阵中已知的评分差异最小 => 最优化问题

我们最终的目的是使求得的打分矩阵loss最小

这里讲一下算数平均值，我们做实验经常用到算数平均值，其实算数平均值最终的原理也是最小二乘法

为什么算数平均值为实际值

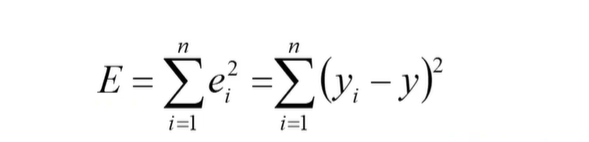
导数为0的时候为最小值，因此

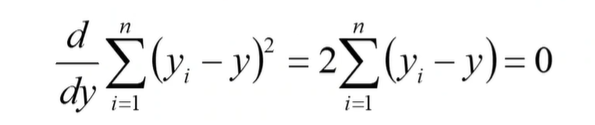
也就是：

所以：

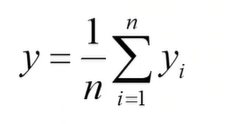
最小二乘法是一种重要的数据拟合技术
可以应用于线性回归，非线性回归

之所以叫交替最小二乘法，是因为同时求X和Y两个矩阵，所以需要固定X求Y，再固定Y求X

1、固定Y优化X

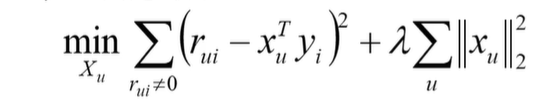
将目标函数转化为矩阵表达形式

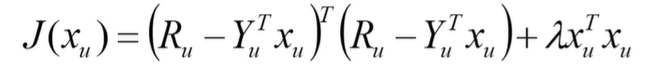
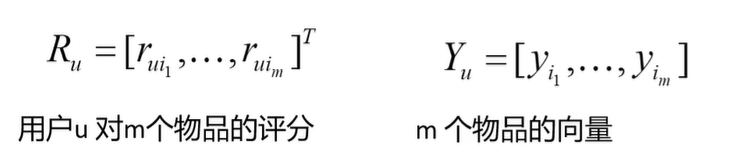
对目标函数 յ关于 xu 求梯度，并令梯度为零，得

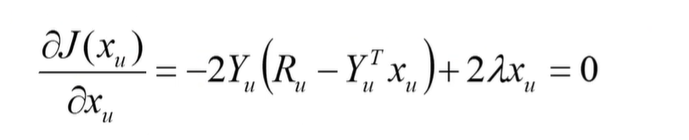
求解后，得：

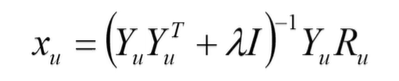
$$x_u=(Y_u{Y}^T+\lambda I{)}^{-1}{Y}_u{R}_u$$

2、固定X优化Y
同理，求解得
$$y_i=(X_u{X}^T+\lambda I{)}^{-1}{X}_u{R}_u$$

然后交替迭代：

• 初始化X,Y
• 利用for u=1,…,n do $$\frac{{\partial }^{}Loss(X,Y)}{\partial x_u^{}}$$=0 去得到xu
• 利用for i=1,…,m do $$\frac{{\partial }^{}Loss(X,Y)}{\partial y_i^{}}$$=0 去得到yi
• 重复2和3，不断去更新直到均方根误差RMSE收敛