- 1【Python】如何在服务器上优雅的部署Python项目(Linux/Windows/Mac)_服务器部署python
- 2100 家企业软件测试笔试面试题汇总(网友真实面试后征集)_软件面试笔试题
- 3Hive介绍与环境搭建
- 4Linux——进程退出_linux退出当前进程
- 5使用solrj连接solrcloud时出现错误:NoNodeException: KeeperErrorCode = NoNode for /clusterstate.json的解决办法_nonodeexception keepererrorcode = nonode for
- 6SDK接口远程调试【内网穿透】_javasdk里面怎么调用远程服务
- 7常见处理器MCU、MPU、DSP、FPGA等嵌入式处理器概念_mcu、mpu、arm、fpga、dsp概念
- 8Java实现音频转文本(语音识别)_java cv语音识别
- 9文字生成图像内容解决方案,享受创作的乐趣
- 10【hiprint】hiprint的使用方法(附使用案例)hiprint 表格数据传输问题解决办法_hiprint官网
带环链表详解_链表有环
赞
踩
目录
一、什么是环形链表
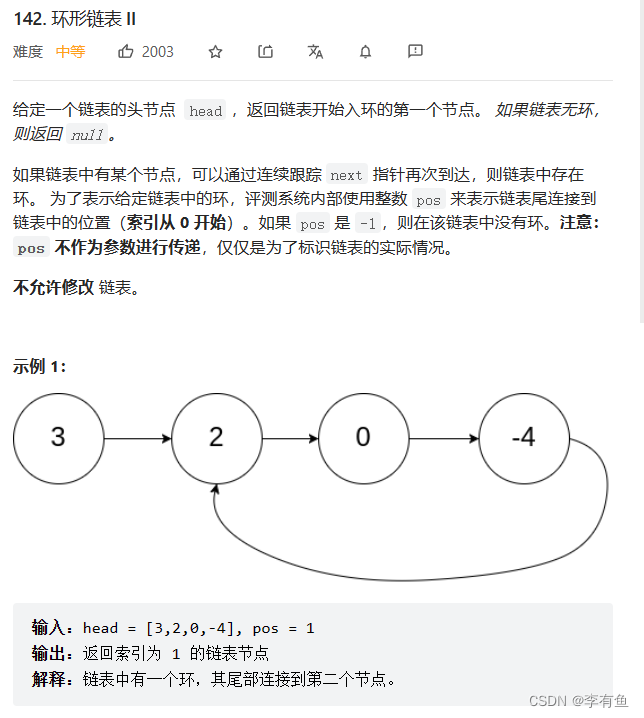
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。
例如下图就是一个环形链表:
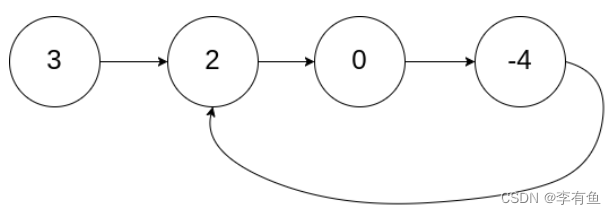
二、判断是否为环形链表
2.1 具体题目
这里我们主要通过一个题来描述:
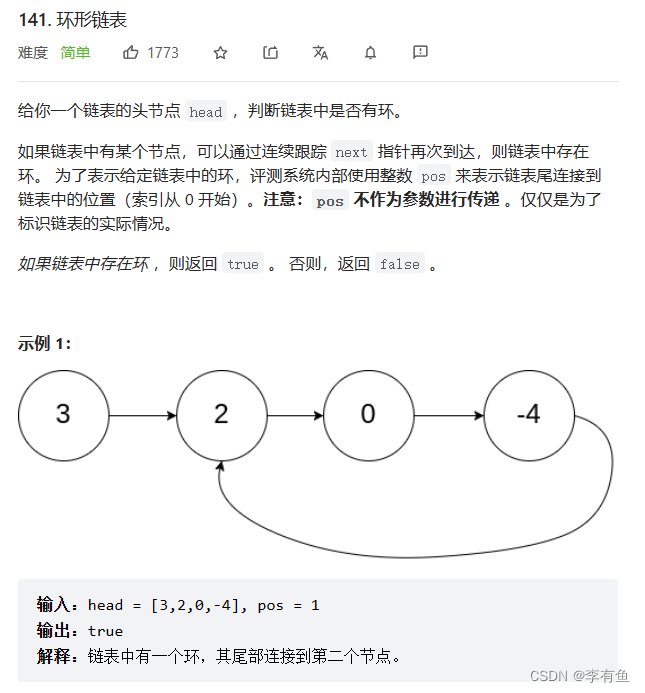
2.2 具体思路
对于判断是否是环形链表这个题,我们提供一个思路并在下文给出关于这个思路的证明。
主题思想是使用快慢指针,如果是带环链表慢指针slow每次走一步,快指针fast每次走两步,slow走到中间位置,fast就进环了,当slow进环时,fast可能已经在环内走了几圈了,此时就变成了追击问题,slow和fast会相遇。如果链表无环,fast会先走到空。
2.3 思路的证明
我们首先提出这两个问题:
- 为什么slow走一步,fast走两步,他们会相遇?会不会错过?请证明。
- 为什么slow走一步,fast走x步(x>=3),他们会相遇?会不会错过?请证明。
2.3.1 证明一
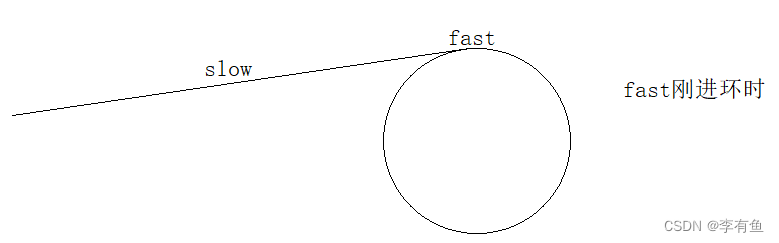
slow刚刚进环时,假设fast与slow之间的距离是N。
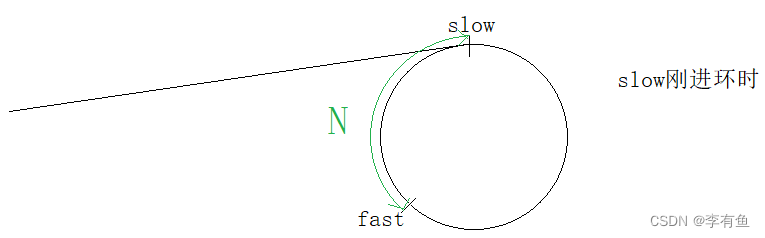
slow进环以后,slow每走一步,fast走两步,他们之间的距离每次缩小一。

slow和fast之间的距离每次缩小一,在slow刚刚进环的时候,slow和fast之间相差N,每次距离-1,总会 减到0,即相遇。
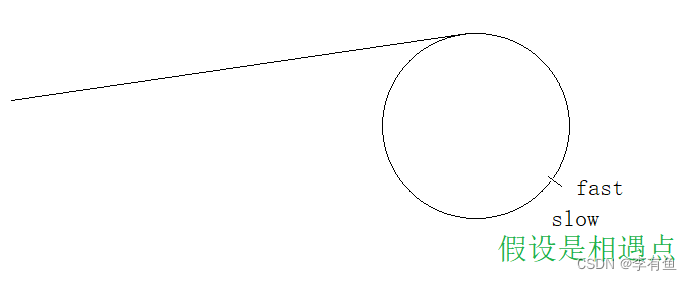
2.3.2 证明二
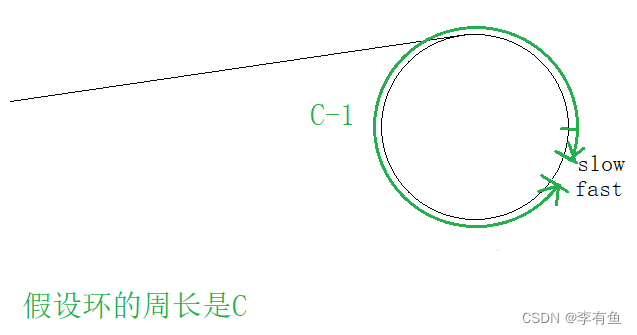
在这里我们以slow走一步,fast走三步来举例证明:
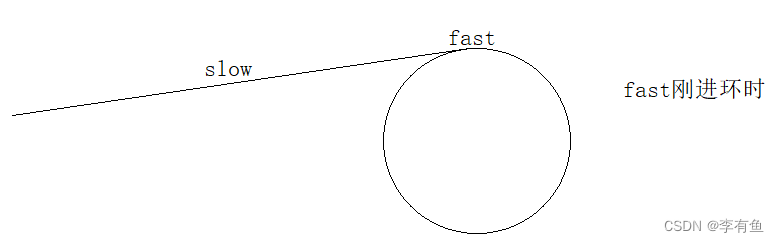
slow刚刚进环时,假设fast与slow之间的距离是N。
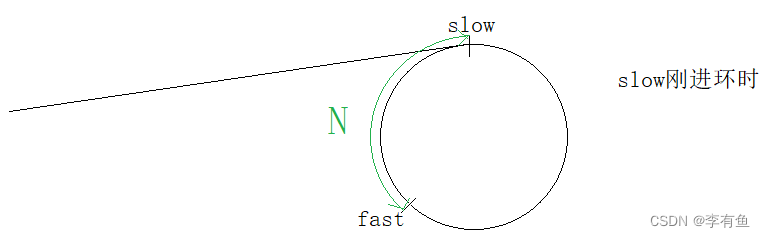
slow进环以后,slow每走一步,fast走三步,他们之间的距离每次缩小二。
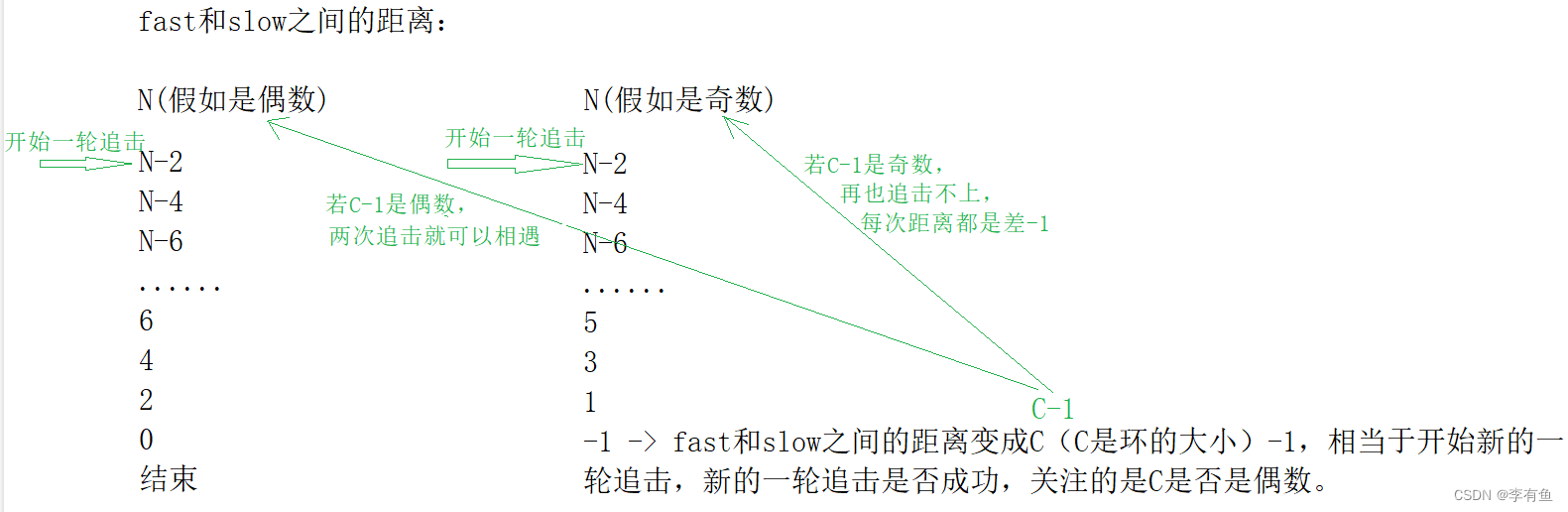
2.3.3 总结
slow和fast是否会相遇主要关注的是他们每走一步之间的距离差,如果他们之间的距离是1,那么他们肯定能够相遇,其他距离差不确定能不能相遇,看环的长度即其他因素。
2.4 代码
- bool hasCycle(struct ListNode *head) {
- struct ListNode * slow = head;
- struct ListNode * fast = head;
- while(fast&&fast->next)
- {
- slow = slow->next;
- fast = fast->next->next;
- if(slow==fast)
- {
- return true;
- }
- }
- return false;
- }
三、求环的长度

slow走一步,fast走两步,走到相遇的位置时,slow再次从相遇位置走一圈,当再次走到相遇位置时正好一圈。
四、求入环的第一个结点
求入环的第一个结点有两个方法,有一个方式需要进行证明。
4.1 结论法(L=N*C-x)
这种方法需要进行证明:
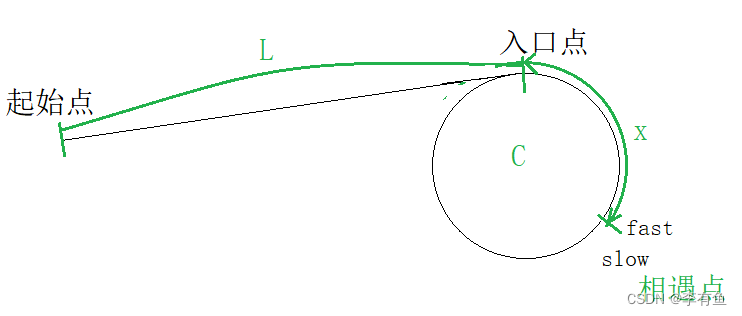
假设:起始点到入口点的距离是L,入口点到相遇点的距离是x,环的长度是C,slow走的距离是L+X,fast走的距离是L+N*C+X,注意的是这里会有一些人认为fast走的距离是L+C+X,这样得出的结论是正确的,但是本质上是对链表认识不清导致的。
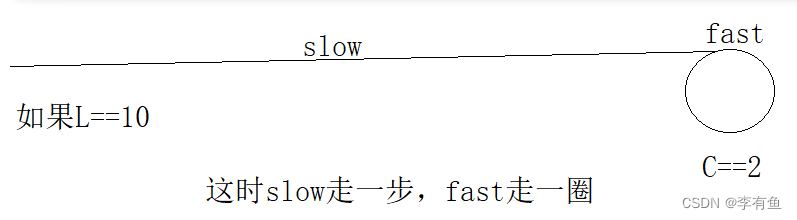
如果是上述的情况,那么slow走L+X,fast不可能只走L+C+X,显然错误。
slow走的距离是L+X,fast走的距离是L+N*C+X,slow每次走一步,fast每次走两步,slow走的路程是fast走的路程的1/2,即得到下式:2*(L+X)= L+N*C+X,化简得到: L = N * C - X 即
L = (N-1)*C+C-X。
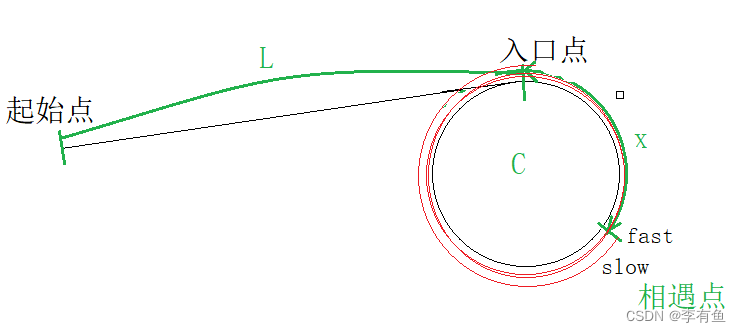
由上面的式子我们可以得出一个结论,一个指针从相遇点走(可能走N圈),一个指针从起始点走(走一次),会在入口点相遇。
代码如下:
- struct ListNode *detectCycle(struct ListNode *head) {
- struct ListNode * h = head;
- struct ListNode * slow = head;
- struct ListNode * fast = head;
- while(fast&&fast->next)
- {
- slow = slow->next;
- fast = fast->next->next;
- if(slow==fast)
- {
- while(slow!=h)
- {
- h = h->next;
- slow = slow->next;
- }
- return slow;
- }
- }
- return NULL;
- }
4.2 转换为相交问题
把相遇点和相遇点的下一个结点之间的链接断开,一个指针从起始点开始走,一个指针从相遇点的下一个指针开始走,转换成相交链表求交点的问题。
让相遇点和相遇点的下一个结点之间的链接断开。

代码:
-
- struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
- struct ListNode* n1 = headA;
- struct ListNode* n2 = headB;
- int x1 = 0;
- int x2 = 0;
- while(n1)
- {
- x1++;
- n1 = n1->next;
- }
-
- while(n2)
- {
- x2++;
- n2 = n2->next;
- }
- if(n1!=n2)
- return NULL;
- int x = abs(x1-x2);
- struct ListNode * shortList = headA,*longList = headB;
- if(x1>x2)
- {
- shortList = headB;
- longList = headA;
- }
- while(x--)
- {
- longList = longList->next;
- }
-
- while(longList!=shortList)
- {
- longList = longList->next;
- shortList = shortList->next;
- }
-
- return longList;
-
- }
-
- struct ListNode *detectCycle(struct ListNode *head) {
- struct ListNode * fast,*slow;
- fast = slow = head;
- while(fast&&fast->next)
- {
- slow = slow->next;
- fast = fast->next->next;
- if(slow == fast)
- {
- struct ListNode *meet = slow;
- struct ListNode *lt1 = meet->next;
- struct ListNode *lt2 = head;
- meet->next = NULL;
- return getIntersectionNode(lt1,lt2);
- }
- }
- return NULL;
- }


