图的应用【最短路径】 —— Floyd 算法_floyd算法求最短路径

图的应用【最短路径】 —— Floyd 算法

Dijkstra算法用于求从源点到其他各个节点的最短路径。

如果求解任意两个节点之间的最短路径，则需要以每个节点为源点，重复调用n次Dijkstra算法。

其实完全没必要这么麻烦，Floyd算法可用于求解任意两个节点间的最短路径。Floyd算法又被称为插点法，其算法核心是在节点i 与节点j 之间插入节点k ，看看是否可以缩短节点i 与节点j之间的距离（松弛操作）。

【算法步骤】

① 数据结构。设置地图的带权邻接矩阵为G .Edge[][]，即如果从节点i 到节点j 有边，则G .Edge[i ][j ]=<i ,j >的权值，否则G.Edge[i ][j ]=∞（无穷大）；采用两个辅助数组：最短距离数组dist[i ][j ]，记录从节点i 到节点j 的最短路径长度；前驱数组p [i][j ]，记录从节点i 到节点j 的最短路径上节点j 的前驱。

② 初始化。初始化dist[i ][j ]=G .Edge[i ][j ]，如果从节点i 到节点j 有边相连，则初始化p [i ][j ]=i ，否则p [i ][j]=-1。

③ 插点。其实就是在节点i 、j 之间插入节点k ，看是否可以缩短节点i 、j 之间的距离（松弛操作）。如果dist[i ][j ]>dist[i][k ]+dist[k ][j ]，则dist[i ][j ]=dist[i ][k ]+dist[k ][j ]，记录节点j 的前驱p [i ][j ]=p [k ][j ]。

【完美图解】

有一个景点地图，如下图所示，

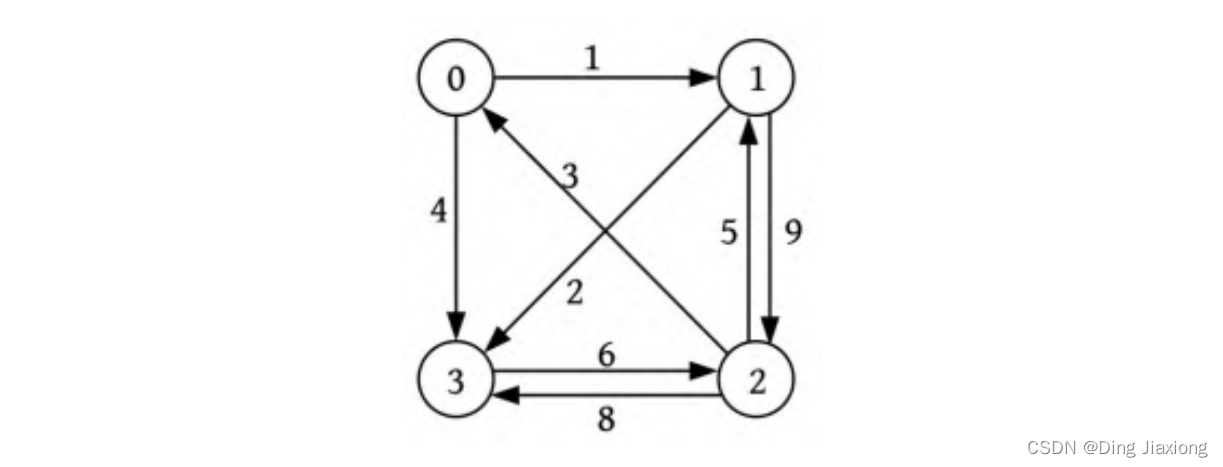
假设从节点0出发，求各个节点之间的最短路径。

1 数据结构。地图采用邻接矩阵存储，如果从节点i 到节点j有边，则G .Edge[i ][j ]=<i , j >的权值；当i =j 时，G .Edge[i ][i ]=0,否则G .Edge[i ][j ]=∞（无穷大）。

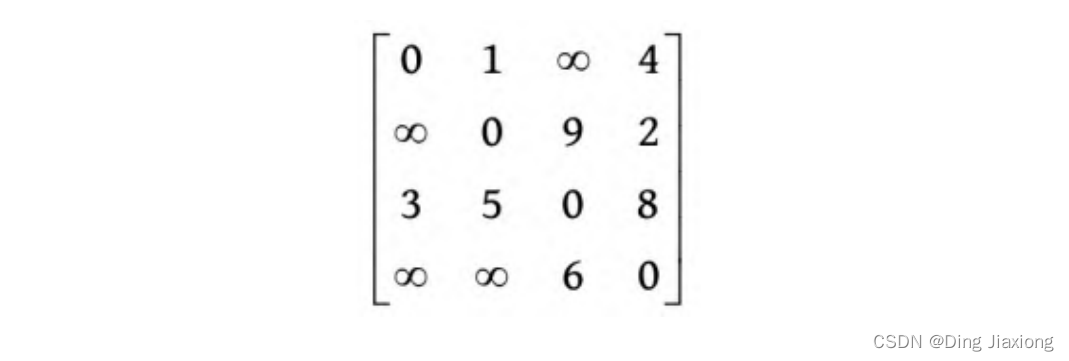
2 初始化。初始化最短距离数组dist[i ][j ]=G .Edge[i ][j]，如果从节点i 到节点j 有边相连，则初始化前驱数组p [i ][j ]=i，否则p [i ][j ]=-1。初始化后的dist[][]和p [][]如下图所示。

3 插点（k =0）。其实就是“借点、借东风”，考查所有节点是否可以借助节点0更新最短距离。如果dist[i ][j ]>dist[i ][0]+dist[0][j ]，则dist[i ][j ]=dist[i ][0]+dist[0][j ]，记录节点j 的前驱为p [i ][j ]=p [0][j ]。谁可以借节点0呢？看节点0的入边2-0，也就是说节点2可以借节点0，更新2到其他节点的最短距离（在程序中需要穷举所有节点是否可以借助节点0）。

• dist[2][1]：dist[2][1]=5>dist[2][0]+dist[0][1]=4，更新dist[2][1]=4，p [2][1]=0。在节点2、1之间插入节点0。
• dist[2][3]：dist[2][3]=8>dist[2][0]+dist[0][3]=7，更新dist[2][3]=7，p [2][3]=0。在节点2、3之间插入节点0。

以上两个最短距离的更新如下图所示。

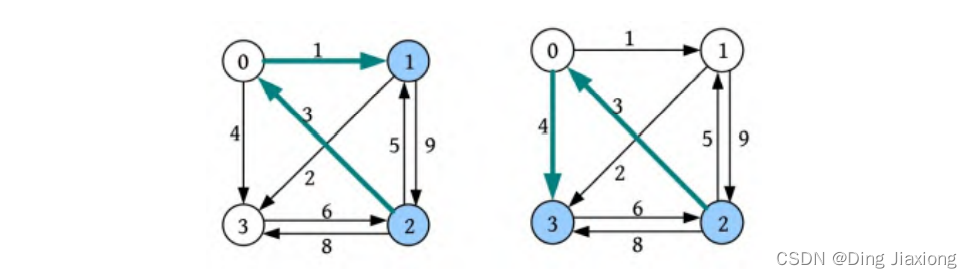
更新后的最短距离数组和前驱数组如下图所示。

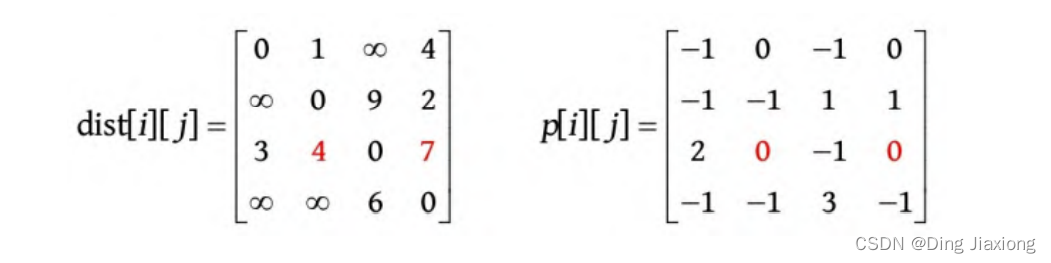
4 插点（k =1）。考查所有节点是否可以借助节点1更新最短距离。看节点1的入边，节点0、2都可以借助节点1更新其到其他节点的最短距离。

• dist[0][2]：dist[0][2]=∞>dist[0][1]+dist[1][2]=10，更新dist[0][2]=10，p [0][2]=1。在节点0、2之间插入节点1。
• dist[0][3]：dist[0][3]=4>dist[0][1]+dist[1][3]=3，更新dist[0][3]=3，p [0][3]=1。在节点0、3之间插入节点1。
• dist[2][0]：dist[2][0]=3<dist[2][1]+dist[1][0]=∞，不更新。
• dist[2][3]：dist[2][3]=8>dist[2][1]+dist[1][3]=6，更新dist[0][2]=6，p [2][3]=1。在节点2、3之间插入节点1。

以上3个最短距离的更新如下图所示。

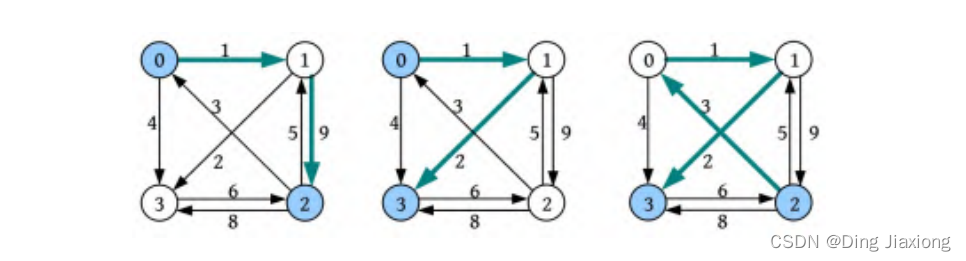
更新后的最短距离数组和前驱数组如下图所示。

5 插点（k =2）。考查所有节点是否可以借助节点2更新最短距离。看节点2的入边，节点1、3都可以借节点2更新其到其他节点的最短距离。

• dist[1][0]：dist[1][0]=∞>dist[1][2]+dist[2][0]=12，更新dist[1][0]=12，p [1][0]=2。在节点1、0之间插入节点2。
• dist[1][3]：dist[1][3]=2<dist[1][2]+dist[2][3]=15，不更新。
• dist[3][0]：dist[3][0]=∞>dist[3][2]+dist[2][1]=9，更新dist[3][0]=9，p [3][0]=2。在节点3、0之间插入节点2。
• dist[3][1]：dist[3][1]=∞>dist[3][2]+dist[2][1]=10，更新dist[3][1]=10，p [3][1]=p[2][1]=0。在节点3、1之间插入节点2。

以上3个最短距离的更新如下图所示。

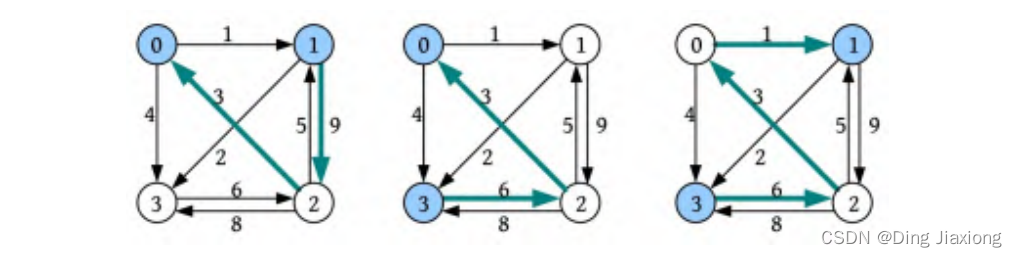
更新后的最短距离数组和前驱数组如下图所示。

6 插点（k =3）。考查所有节点是否可以借助节点3更新最短距离。看节点3的入边，节点0、1、2都可以借助节点3更新其到其他节点的最短距离。

• dist[0][1]：dist[0][1]=1<dist[0][3]+dist[3][1]=13，不更新。
• dist[0][2]：dist[0][2]=10>dist[0][3]+dist[3][2]=9，更新dist[0][2]=9，p [0][2]=3。在节点0、2之间插入节点3点。
• dist[1][0]：dist[1][0]=12>dist[1][3]+dist[3][0]=11，更新dist[1][0]=11，p [1][0]=p [3][0]= 2。在节点1、0之间插入节点3。
• dist[1][2]：dist[1][2]=9>dist[1][3]+dist[3][2]=8，则更新dist[1][2]=8，p [1][2]=3。在节点1、2之间插入节点3。
• dist[2][0]：dist[2][0]=3<dist[2][3]+dist[3][0]=15，不更新。
• dist[2][1]：dist[2][1]=4<dist[2][3]+dist[3][1]=16，不更新。

以上3个最短距离的更新如下图所示。

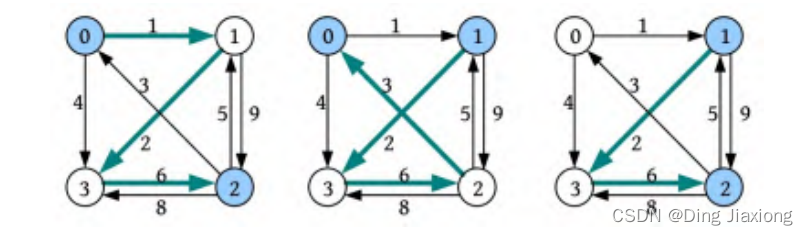
更新后的最短距离数组和前驱数组如下图所示。

7 插点结束。dist[][]数组包含了各节点之间的最短距离，如果想找从节点i 到节点j 的最短路径，则可以根据前驱数组p [][]找到。例如，求从节点1到节点2的最短路径，首先读取p [1][2]=3，说明节点2的前驱为节点3，继续向前找，读取p [1][3]=1，说明节点3的前驱为节点1，得到从节点1到节点2的最短路径为1-3-2。求从节点1到节点0的最短路径，首先读取p [1][0]=2，说明节点0的前驱为节点2，继续向前找，读取p [1][2]=3，说明节点2的前驱为节点3，继续向前找，读取p [1][3]=1，得到从节点1到节点0的最短路径为1-3-2-0。

【算法实现】

void Floyd(AMGragh G){ //用Flody算法求有向图G 中各对节点i 与 j 之间的最短路径
	int i , j , k;
	for(i = 0 ; i < G.vexnum ; i++){ //各对节点之间的初始距离及已知路径
		for(j = 0 ; j < G.vexnum ; j ++){
			dist[i][j] = G.Edge[i][j];
			if(dist[i][j] < INF && i != j){
				p[i][j] = i; //如果在节点i 和 节点j 之间有弧，则将节点j 的前驱置为i
			}
			else{
				p[i][j] =  -1; //如果在节点i 和 节点 j 之间无弧，则将节点j 的前驱置为-1
			}
		}
	}
	for(k = 0 ; k < G.vexnum ; k ++){
		for(i = 0 ; i < G.vexnum ; i++){
			for(j = 0 ; j < G.vexnum ; j ++){
				if(dist[i][k] + dist[k][j] < dist[i][j]){ //从节点i 经节点k 到节点j 的一条路径更短
					dist[i][j] = dist[i][k] + dist[k][j]; //更新dist[i][j]
					p[i][j] = p[k][j]; //更改j 的前驱为k	
				}
			}
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

【算法分析】

时间复杂度：三层for循环，时间复杂度为O (n^3 )。

空间复杂度：采用最短距离数组dist[][]和前驱数组p[][]，空间复杂度为O (n^2 )。

尽管Floyd算法的时间复杂度为O (n^3 )，但其代码简单，对于中等输入规模来说，仍然相当有效。如果用Dijkstra算法求解各个节点之间的最短路径，则需要以每个节点为源点都调用一次，共调用n 次，其总的时间复杂度也为O (n^3 )。

特别注意的是，Dijkstra算法无法处理带有负权边的图。如果有负权边，则可以采用Bellman-Ford算法或SPFA算法。