BTree与B+Tree图文详解_btree演示图

一、前言

磁盘I/O：是指磁盘的输入和输出(Input和Output的缩写)。 

二叉查找树：左子树的键值小于根的键值，右子树的键值大于根的键值。 

二叉查找树可以任意地构造，同样是2,3,5,6,7,8这六个数字，也可以按照下图的方式来构造： 

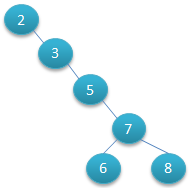
由图1和图2来查找数字8，深度很明显有差距，所以其查找的时间复杂度O(log2N)与树的深度相关，那么降低树的深度自然会提高查找效率。 因此若想二叉树的查询效率尽可能高，需要这棵二叉树是平衡的，从而引出新的定义——平衡二叉树，或称AVL树。

平衡二叉树 ：

平衡二叉树（AVL树）在符合二叉查找树的条件下，还满足任何节点的两个子树的高度最大差为1。下面的两张图片，左边是AVL树，它的任何节点的两个子树的高度差<=1；右边的不是AVL树，其根节点的左子树高度为3，而右子树高度为1；

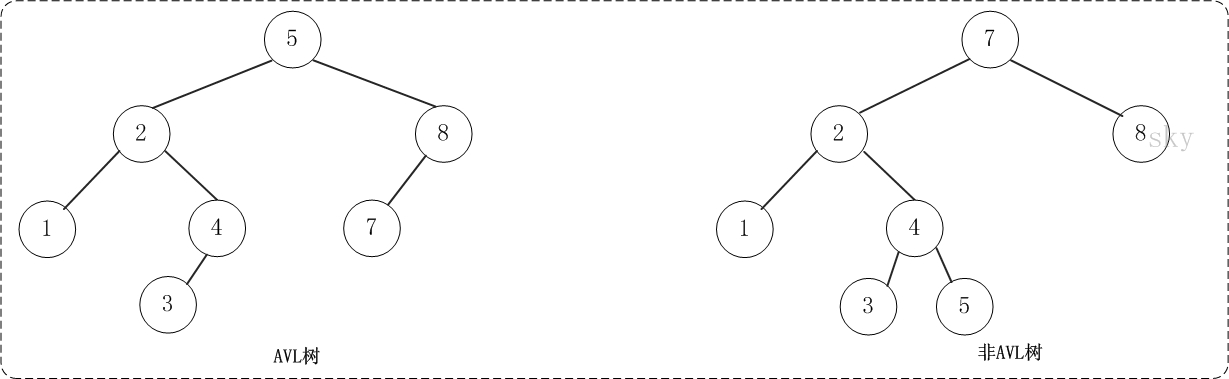
但是平衡二叉树在删除或者新增节点时可能会失去平衡

二叉查找树结构会因树的深度过大而造成磁盘I/O读写过于频繁，进而导致查询效率低下

二、平衡多路查找树（B-Tree）

B-Tree是为磁盘等外存储设备设计的一种平衡查找树,系统从磁盘读取数据到内存时是以磁盘块（block）为基本单位的，位于同一个磁盘块中的数据会被一次性读取出来，而不是需要什么取什么。

B-Tree结构的数据可以让系统高效的找到数据所在的磁盘块。为了描述B-Tree，首先定义一条记录为一个二元组[key, data] ，key为记录的键值，对应表中的主键值，data为一行记录中除主键外的数据。对于不同的记录，key值互不相同。

一棵m阶的B-Tree有如下特性： 

• 每个节点最多有m个孩子。 
• 除了根节点和叶子节点外，其它每个节点至少有Ceil(m/2)个孩子。 
• 若根节点不是叶子节点，则至少有2个孩子 
• 所有叶子节点都在同一层，且不包含其它关键字信息 
• 每个非终端节点包含n个关键字信息（P0,P1,…Pn, k1,…kn） 
• 关键字的个数n满足：ceil(m/2)-1 <= n <= m-1 
•  ki(i=1,…n)为关键字，且关键字升序排序。 
• Pi(i=1,…n)为指向子树根节点的指针。P(i-1)指向的子树的所有节点关键字均小于ki，但都大于k(i-1)

它的每一个节点最多包含m个孩子，m便称为B树的阶。m的大小取决于磁盘页的大小。

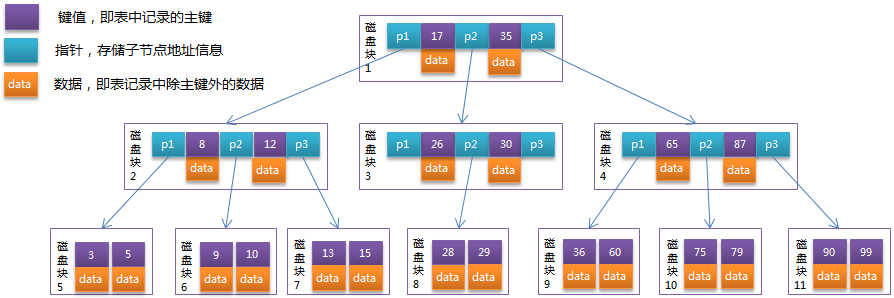
以根节点为例，关键字为17和35，P1指针指向的子树的数据范围为小于17，P2指针指向的子树的数据范围为17~35，P3指针指向的子树的数据范围为大于35。

三、B+Tree

B+Tree是在B-Tree基础上的一种优化，使其更适合实现外存储索引结构，InnoDB存储引擎就是用B+Tree实现其索引结构。

B+Tree相对于B-Tree有几点不同：

1. 非叶子节点只存储键值信息。
2. 所有叶子节点之间都有一个链指针。
3. 数据记录都存放在叶子节点中。

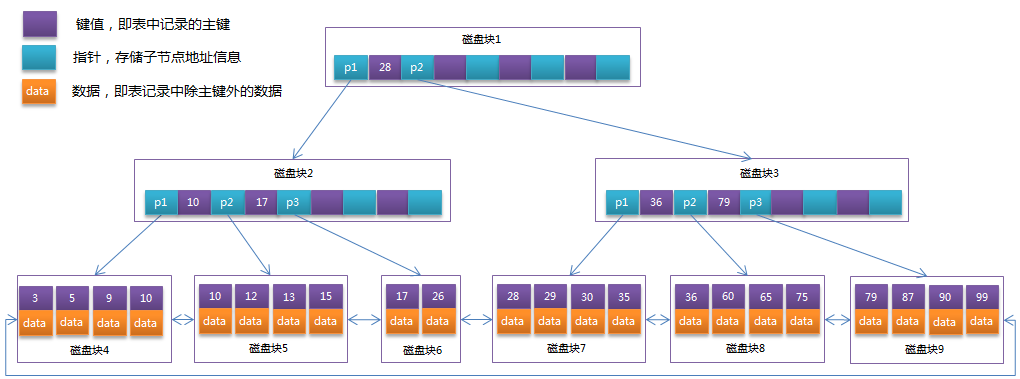
 通常在B+Tree上有两个头指针，一个指向根节点，另一个指向关键字最小的叶子节点，而且所有叶子节点（即数据节点）之间是一种链式环结构。因此可以对B+Tree进行两种查找运算：一种是对于主键的范围查找和分页查找，另一种是从根节点开始，进行随机查找。