最长回文子串（Java版本）_最长回文子串java

目录

1、题目

2、示例

3、解决方案

3.0 暴力破解

3.1 动态规划

3.2 中心扩展算法

3.3 Manacher 算法

4.参考

---

1、题目

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

2、示例

示例 1：
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
 
示例 2：
输入: "cbbd"
输出: "bb"

3、解决方案

3.0 暴力破解

这应该是在没有其他解法的时候，你应该想到的：暴力求解，列举所有的子串，判断是否为回文串，保存最长的回文串。

    public static String longestPalindrome(String s) {
        String ans = "";
        int max = 0;
        int len = s.length();
        for (int i = 0; i < len; i++) {
            for (int j = i + 1; j <= len; j++) {
                String tmp = s.substring(i, j);
                if (isPalindromic(tmp) && tmp.length() > max) {
                    ans = tmp;
                    max = j - i;
                }
            }
        }
        return ans;
    }
 
    private static boolean isPalindromic(String s) {
        int len = s.length();
        for (int i = 0; i < len / 2; i++) {
            if (s.charAt(i) != s.charAt(len - i - 1)) {
                return false;
            }
        }
        return true;
    }

时间复杂度：两层 for 循环 O(n²），for 循环里边判断是否为回文 O(n），所以时间复杂度为 O(n³）。

空间复杂度：O(1），常数个变量。

3.1 动态规划

暴力解法时间复杂度太高，我们可以考虑，去掉一些暴力解法中重复的判断。

首先定义：字符串 s 从下标 i 到下标 j 的字串为 P(i, j)，若 s 从下标 i 到下标 j 的字串为回文串，则 P(i, j) = true，否则 P(i, j) = false。如下图所示：

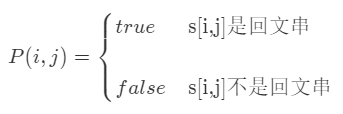
则 P(i, j) = (P(i + 1, j - 1) && s[i] == s[j])。

所以如果我们想知道 P（i,j）的情况，不需要调用判断回文串的函数了，只需要知道 P（i+1，j−1）的情况就可以了，这样时间复杂度就少了 O(n)。因此我们可以用动态规划的方法，空间换时间，把已经求出的 P（i，j）存储起来。

如果 s[i+1, j-1] 是回文串，那么只要 s[i] == s[j]，就可以确定 s[i, j] 也是回文串了。

注意：

求 长度为 1 和长度为 2 的 P(i, j) 时不能用上边的公式，因为我们代入公式后会遇到 P[i][j] 中 i > j 的情况，比如求P[1][2] 的话，我们需要知道 P[1+1][2-1]=P[2][1] ，而 P[2][1] 代表着 S[2, 1] 是不是回文串，这显然是不对的，所以我们需要单独判断。

所以我们先初始化长度是 1 的回文串的 P [i , j]，这样利用上边提出的公式 P(i,j)=(P(i+1,j-1) && S[i]==S[j])，然后两边向外各扩充一个字符，长度为 3 的，为 5 的，所有奇数长度的就都求出来了。同理，初始化长度是 2 的回文串 P[i,i+1]，利用公式，长度为 4 的，6 的所有偶数长度的就都求出来了。

    public static String longestPalindrome(String s) {
        int sLen = s.length();
        int maxLen = 0;
        String ans = "";
        boolean[][] P = new boolean[sLen][sLen];
        // 遍历所有长度
        for (int len = 1; len <= sLen; len++) {
            for (int start = 0; start < sLen; start++) {
                int end = start + len - 1;
                // 下标越界，结束循环
                if (end >=sLen) {
                    break;
                }
                P[start][end] = (len == 1 || len == 2 || P[start + 1][end - 1]) && s.charAt(start) == s.charAt(end);
                if (P[start][end] && len > maxLen) {
                    maxLen = len;
                    ans = s.substring(start, end + 1);
                }
            }
        }
        return ans;
    }

时间复杂度：两层循环 O(n²）。

空间复杂度：用二维数组 PP保存每个子串的情况 O(n²)。

下面分析空间使用情况：（以”babad“为例）

当我们求长度为 5  的子串的情况时，其实只用到了 4 长度的情况，而长度为 1 和 2  和 3 的子串情况其实已经不需要了。

但是由于我们并不是用 P 数组的下标进行的循环，暂时没有想到优化的方法。

那么我们换种思路，公式不变：

其实从递推公式中我们可以看到，我们首先知道了 i +1 才会知道 i ，所以我们只需要倒着遍历就行了。

    public static String longestPalindrome(String s) {
        int sLen = s.length();
        String ans = "";
        boolean[][] P = new boolean[sLen][sLen];
 
        for (int i = sLen - 1; i >= 0; i--) {
            for (int j = i; j < sLen; j++) {
                P[i][j] = (s.charAt(i) == s.charAt(j)) && (j - i < 2 || P[i + 1][j - 1]);
                if (P[i][j] && j - i + 1 > ans.length()) {
                    ans = s.substring(i, j + 1);
                }
            }
        }
        return ans;
    }

时间复杂度和空间复杂和之前都没有变化，我们来看看可不可以优化空间复杂度。

当求第 i 行的时候我们只需要第 i+1 行的信息，并且 j 的话需要 j−1 的信息，所以和之前一样 j 也需要倒序。

    public static String longestPalindrome(String s) {
        int sLen = s.length();
        String ans = "";
        boolean[] P = new boolean[sLen];
 
        for (int i = sLen - 1; i >= 0; i--) {
            for (int j = sLen - 1; j >= i; j--) {
                P[j] = s.charAt(i) == s.charAt(j) && (j - i < 2 || P[j - 1]);
                if (P[j] && j - i + 1 > ans.length()) {
                    ans = s.substring(i, j + 1);
                }
            }
        }
 
        return ans;
    }

时间复杂度：不变 O(n²）。

空间复杂度：降为 O(n )。

3.2 中心扩展算法

我们知道回文串一定是对称的，所以我们可以每次循环选择一个中心，进行左右扩展，判断左右字符是否相等即可。

由于存在奇数的字符串和偶数的字符串，所以我们需要从一个字符开始扩展，或者从两个字符之间开始扩展，所以总共有

n + （n-1）个中心。

    public static String longestPalindrome(String s) {
        if (s == null || s.length() < 1) {
            return "";
        }
        int start = 0, end = 0;
        for (int i = 0; i < s.length(); i++) {
            int len1 = expandAroundCenter(s, i, i);
            int len2 = expandAroundCenter(s, i, i+1);
 
            int len = Math.max(len1, len2);
            if (len > end - start) {
                start = i - (len-1) / 2;
                end = i + len / 2;
            }
        }
 
        return s.substring(start, end + 1);
    }
 
    public static  int expandAroundCenter(String s, int left, int right) {
        int L = left, R = right;
        while (L >= 0 && R < s.length() && s.charAt(L) == s.charAt(R)) {
            L--;
            R++;
        }
        return (R-1) - (L+1) + 1;
    }

3.3 Manacher 算法

https://www.cnblogs.com/bitzhuwei/p/Longest-Palindromic-Substring-Part-II.html

4.参考

https://leetcode-cn.com/problems/longest-palindromic-substring/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-bao-gu/

https://www.cnblogs.com/bitzhuwei/p/Longest-Palindromic-Substring-Part-II.html