- 1程序员入门培训班多少钱?可以学到哪些东西?_程序员培训班要多少钱
- 2jwt 介绍_怎么查看一个浏览器网页的jwt
- 32021年危险化学品生产单位安全生产管理人员考试题库及危险化学品生产单位安全生产管理人员考试内容_人体是导体,在静电场中可能接触起电
- 4Vivado工程经验与时序收敛技巧_vivado fix cell
- 5算法——动态规划_完全加括号是什么意思
- 6git代码库迁移保留commit历史_Git 如何迁移仓库并保留 commit 记录
- 7RK3328 Debian安装OpenMediaVault
- 8git 拉取代码时显示Filename too long的解决办法_git file name too long
- 9系统盘50G,数据盘100G(需求:将数据磁盘扩容至1T)_系统盘和数据盘配比
- 10WooCommerce入门指南:简介
动态规划_完全背包问题_动态规划求解完全背包问题
赞
踩
描述
设有 n 种物品,每种物品有一个重量及一个价值。但每种物品的数量是无限的,同时有一个背包,最大载重量为 M,今从 n 种物品中选取若干件(同一种物品可以多次选取),使其重量的和小于等于 M,而价值的和为最大。
输入描述
第一行:两个整数,M ( 背包容量,M≤200 )和 N ( 物品数量,N≤30 )。
第 2…N+1 行:每行二个整数 Wi,Ci,表示每个物品的重量和价值。
输出描述
仅一行,一个数,表示最大总价值。
样例输入
- 10 4
- 2 1
- 3 3
- 4 5
- 7 9
样例输出
max=12
数据范围与提示
M≤200,N≤30
完全背包与01背包的区别:
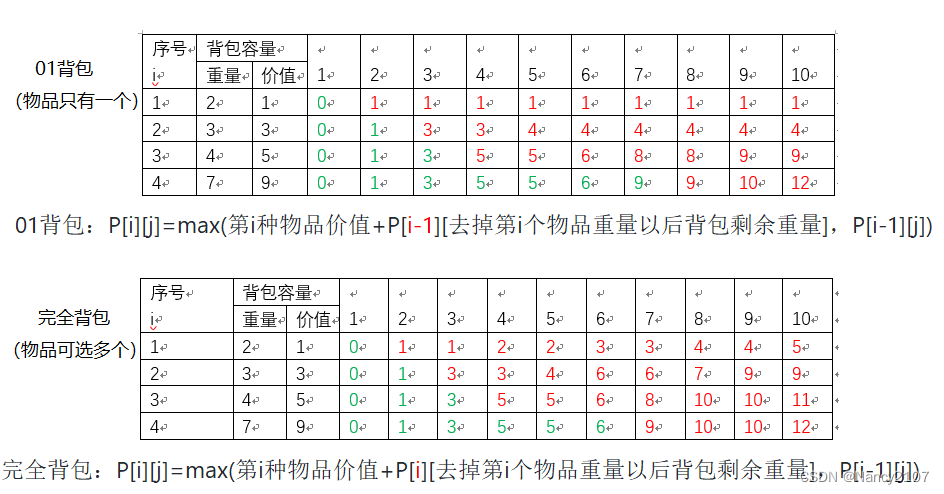
01背包文件解决:动态规划_01背包问题-CSDN博客
完全背包问题解决:
物品编号为i,,背包容量为j ,背包价值为p[i][j]
(1)第一行(i=1)尝试将序号为1的物品放入背包:
背包容量为1时,什么都装不进去背包价值为0,P[1][1]=0。
背包容量为2时,正好1号物品重量为2,背包价值为1,P[1][2]=1。
因为是完全背包问题,物品只有无数,所以第一行后面的背包价值会重新计算:P[i][j]=max(第i种物品价值+P[i][去掉第i个物品重量以后背包剩余重量],P[i-1][j]),如:p[1][4]=max(第1中物品价值为1+p[1][背包价值4-第1个物品重量2],P[0][4])= max(1+p[1][ 4- 2],0)=max(1+p[1][2],0)= max(2,0)
| 序号i | 背包容量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 重量 | 价值 | |||||||||||
| 1 | 2 | 1 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 2 | 3 | 3 | ||||||||||
| 3 | 4 | 5 | ||||||||||
| 4 | 7 | 9 | ||||||||||
(2)第二行(i=2)尝试将序号为1、2的物品放入背包:
背包容量为1时,什么都装不进去背包价值为0,P[2][1]=0。
背包容量为2时,正好1号物品重量为2,背包价值为1,P[2][2]=1。
背包容量为3时,对比第一行是背包价值为1,即 P[1][2]=1。现新增加了第2种物品,新增加的重量为3,正好为背包容量。因此 P[2][3]=3。。
背包容量为4时,也只能放重量为3的物品P[2][4]=3
背包容量为5时,对比第一行是背包价值为1,即 P[1][5]=1。现新增加了第2种物品,背包装上第2种物品后剩余容量为2,正好装第1种物品,因此 P[2][5]=4。P[i][j]=max(第i种物品价值+P[i][ 去掉第i个物品重量以后背包剩余重量],P[i-1][j])=max(p[2][2]+3,p[1][5])=max(1+3,1)=4
依次类推完成表格:
| 序号 i | 背包容量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 重量 | 价值 | |||||||||||
| 1 | 2 | 1 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 2 | 3 | 3 | 0 | 1 | 3 | 3 | 4 | 6 | 6 | 7 | 9 | 9 |
| 3 | 4 | 5 | 0 | 1 | 3 | 5 | 5 | 6 | 8 | 10 | 10 | 11 |
| 4 | 7 | 9 | 0 | 1 | 3 | 5 | 5 | 6 | 9 | 10 | 10 | 12 |
推理:
背包容量为j时,可装入背包的最大价值为:
如果j<第i 物品重量:直接取上方表格背包价值,即p[i][j]= p[i-1][j];
如果j>=第i 物品重量:
P[i][j]=max(P[i][去掉第i个物品重量以后背包剩余重量]+第i种物品价值,P[i-1][j]) 。
实现代码:
- #include <bits/stdc++.h>
- using namespace std;
- int main(){
- int p[201][201] = {},b[201][2] = {} ;//p[201][201]背包价值 b[201][2] 物品重量价值
- int M,N; //M 背包容量,N物品数量
- cin >> M >> N;
- for(int i = 1;i <= N;i++)
- {
- cin >> b[i][0] >> b[i][1];
- }
- for(int i = 1;i <=N;i++)
- {
- for(int j = 1;j <= M;j++)
- {
- if (j < b[i][0])
- {
- p[i][j]=p[i-1][j];
- }
- else
- {
- int val= j-b[i][0];//去掉第i个物品重量以后背包剩余重量
- p[i][j]=max( b[i][1] + p[i][val] , p[i-1][j]) ;
- }
- }
- }
- cout <<"max="<< p[N][M];
- return 0;
- }

代码执行过程:
选择1个产品背包价值:
(1,1)=0 (1,2)=1 (1,3)=1 (1,4)=2 (1,5)=2 (1,6)=3 (1,7)=3 (1,8)=4 (1,9)=4 (1,10)=5
选择1、2个产品背包价值:
(2,1)=0 (2,2)=1 (2,3)=3 (2,4)=3 (2,5)=4 (2,6)=6 (2,7)=6 (2,8)=7 (2,9)=9 (2,10)=9
选择1、2、3个产品背包价值:
(3,1)=0 (3,2)=1 (3,3)=3 (3,4)=5 (3,5)=5 (3,6)=6 (3,7)=8 (3,8)=10 (3,9)=10 (3,10)=11
选择1、2、3、4个产品背包价值:
(4,1)=0 (4,2)=1 (4,3)=3 (4,4)=5 (4,5)=5 (4,6)=6 (4,7)=9 (4,8)=10 (4,9)=10 (4,10)=12


