- 1Rocky Linux 9.4 部署Zabbix 7.0_zabbix7
- 2(三十四)大数据实战——scala运行环境安装配置及IDEA开发工具集成_scala项目实战
- 3在linux下配置与安装mysql-5.6.40_mysql5.6.40
- 4Oracle中的CASE WHEN语句使用详解与实例_oracle的case when语句
- 5对#多种编程语言 性能的研究和思考 go/c++/rust java js ruby python_golang 和 java 和c++ 性能对比
- 6ORB-SLAM3 导航图/编译/运行_orbslam3 快速加载 bin
- 7Fastjson的学习与使用_fastjson github
- 8开源:基于Vue3.3 + TS + Vant4 + Vite5 + Pinia + ViewPort适配..搭建的H5移动端开发模板
- 9香橙派AIpro初体验:搭建无线随身NAS_香橙派aipro连接wifi
- 10java开发工程师—如何让你的简历脱颖而出?(1)_java开发简历怎么写
机器人运动学(四):逆向运动学_机器人逆向运动学
赞
踩
系列文章目录
前言
一、引言
回顾之前学的手臂顺向运行学forward kinematics(FK)
给予
θ
i
\theta_i
θi,求得{H}或
W
P
^WP
WP
H
W
T
=
f
(
θ
1
.
.
.
,
θ
i
,
.
.
.
θ
n
.
.
.
)
W
P
=
H
W
T
H
P
^W_HT = f(\theta_1...,\theta_i,...\theta_n...)\\~\\~ ^WP= ~^W_HT^HP
HWT=f(θ1...,θi,...θn...) WP= HWTHP
今天要学的逆向运动学Inverse Kinematics(IK)
给予{H}或
W
P
^WP
WP,求得
θ
i
\theta_i
θi
[
θ
1
.
.
.
,
θ
i
,
.
.
.
θ
n
.
.
.
]
=
f
−
1
(
H
W
T
)
[\theta_1...,\theta_i,...\theta_n...]=f^{-1}(^W_HT)
[θ1...,θi,...θn...]=f−1(HWT)
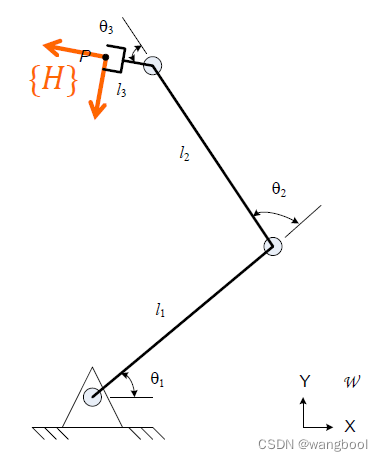
二、求解概念
2.1.分析
- 假设手臂有6DOFs
则有6个未知的joint angles( θ i \theta_i θi或者 d i d_i di,i=1,2,……6)
- 在
H
W
T
^W_HT
HWT中摘取出含未知数的
0
6
T
^6_0T
06T
含有16个数字,除去构成homogeneous transformation matrix的最后一行四个数字,其余十二表示了所有位姿参数。其中左上的九个即为world frame到hand frame的rotation matrix,我们知道旋转只有三个自由度,所有在rotation matrix中有六个限制条件,首先,我们知道rotation Matrix的三个columns即为frame{B}的basis: X B , Y B , Z B X_B,Y_B,Z_B XB,YB,ZB在{A}上的表示,所以前三个的条件为矩阵的每一个columns的范数为1, 由于都是basis,所以后三个限制条件为三个columns两两垂直。在rotation matrix右边的三个为{W}原点到{H}原点的向量,也就是移动的三个自由度。
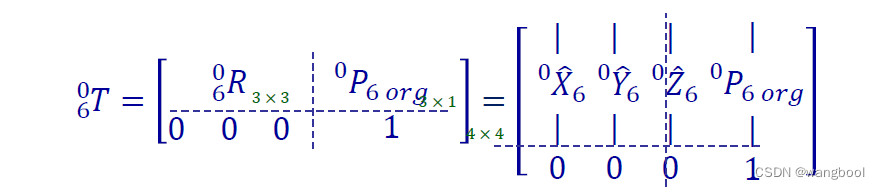
- 求解
十二个nonlinear transcendtal equations方程式
六个未知数,六个限制条件 - Reachable workspace
对空间中手臂可以用一种以上的姿态到达的点的集合。 - Dexterous workspace
对空间中手臂可以用任意姿态到达的点的集合。
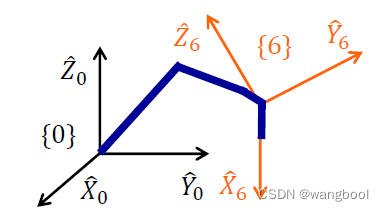
Ex:A RR manipulator

图中,只有 l 1 = l 2 l_1= l_2 l1=l2时的原点是Dexterous workspace
- Subspace
手臂在定义头尾的T所能达到的变动范围。T(可以理解为空间中的位姿)本身在空间中,可以包含的移动和转动可以包含的非常多,但是手臂不是每个都能到得了,可以到的那一些称为这个手臂的Subspace。
Ex:A PRmanipulator
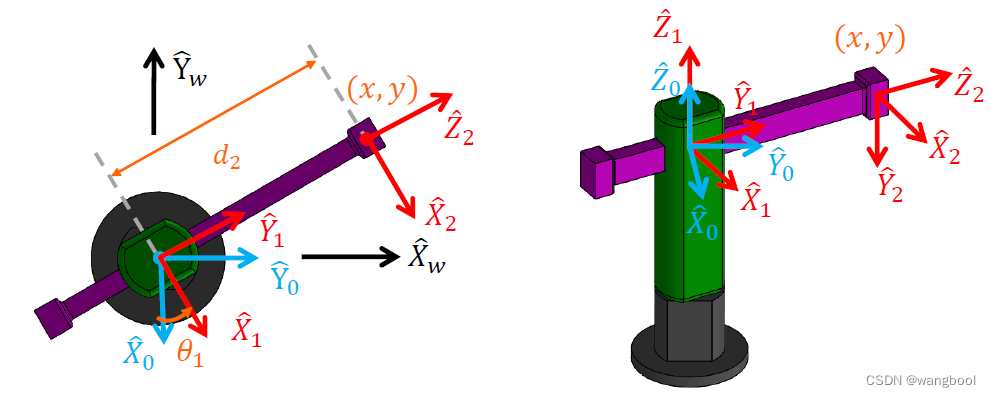
要达到空间中某个(第二个关节的平面上)
(
x
,
y
)
(x,y)
(x,y)坐标点上,当我们决定了x,y后,事实上我们也决定了到达这个点的姿态。
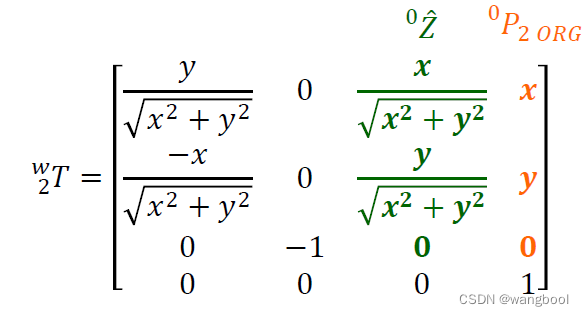
在式中
0
P
o
r
g
^0P_{org}
0Porg是{2}原点在{W}的向量坐标,可以看出,当机械臂到达坐标(x,y)后,{2}Z轴已经确定了,因为只有两个关节,没有多的参数可以调控姿态,所有没办法可以使手臂在(x,y)上有各种姿态到达。换句话说,如式中所示,随着x,y变化的只有第一个和第三个columns的前两个参数,rotation tmatrix剩下的五个参数已经固定,在这个手臂上,与这五个参数不一样的姿态手臂都到达不了。
所以,当手臂的自由度不够的时候,事实上手臂的subspace是非常有限的。所以,在我们对一个手臂的预想某一个位姿,这个手臂到不到得了,可以做一个初步的判断。
二、多重解
2.1.解的数目
以6DOFs为例,由于是nonlinear transcendtal equations,六个未知数六个方程,不一定有唯一解。
解的数目由joint数量和link参数所决定的
Ex:A RRRRRR manipulator
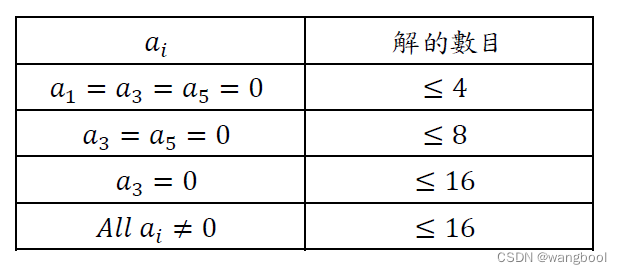
2.2.示例:PUMA(6 rotational joints)
- 针对特定工作点,有8组解
前三轴决定了四种姿态 ,每一种姿态中,具有2组手腕转动姿态,但是若手臂本身有限制,并非每一种解都可以运作。
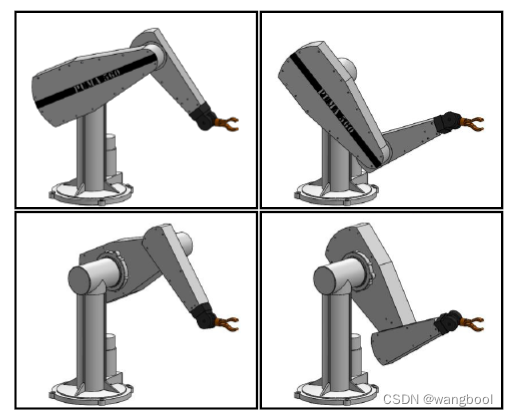
2.3 解的选择
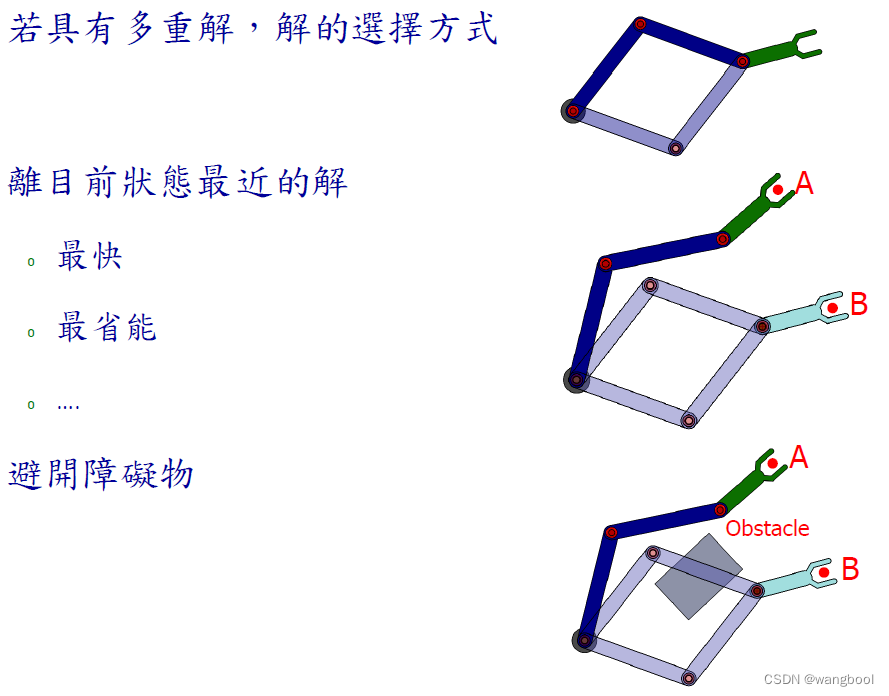
三、求解方法
- 解析法Closed-form solutions
用代数algebraic或几何geometric方法 - 数值法Numerical solutions
目前大多数机械手臂设计成具有解析解,求解的速度会快很多。如果将相邻的后三轴设计成相交于一点,那么就很可能有解析解,也就是我们说的Pieper‘s solution。
四、Example
4.1 A RRR Manipulator

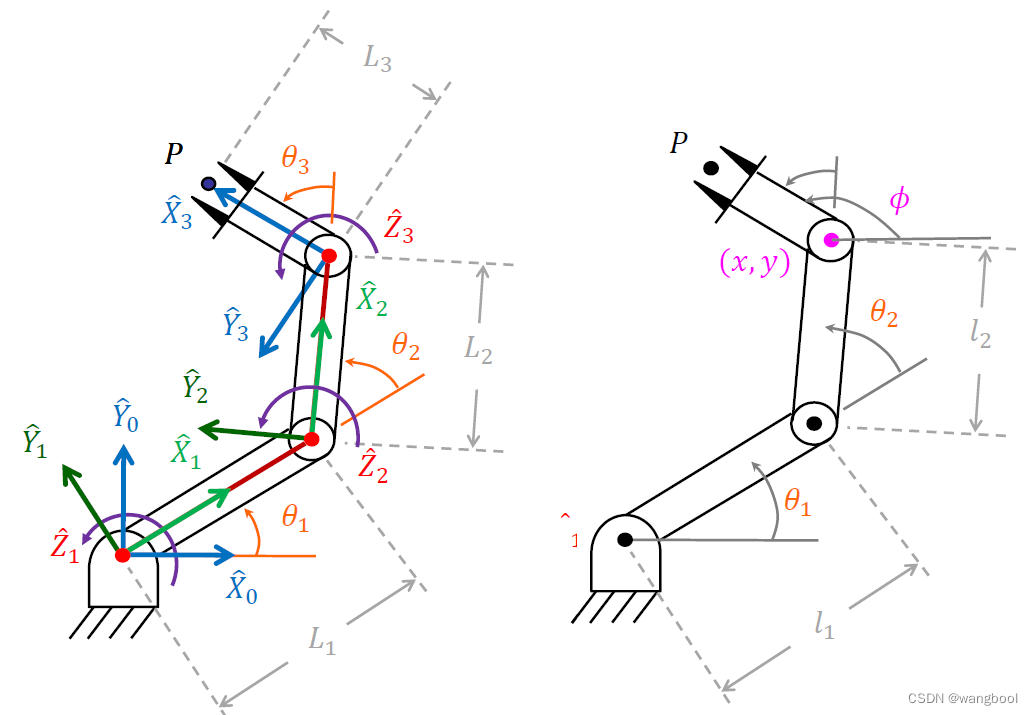
4.1.几何法:将空间几何切割成平面几何
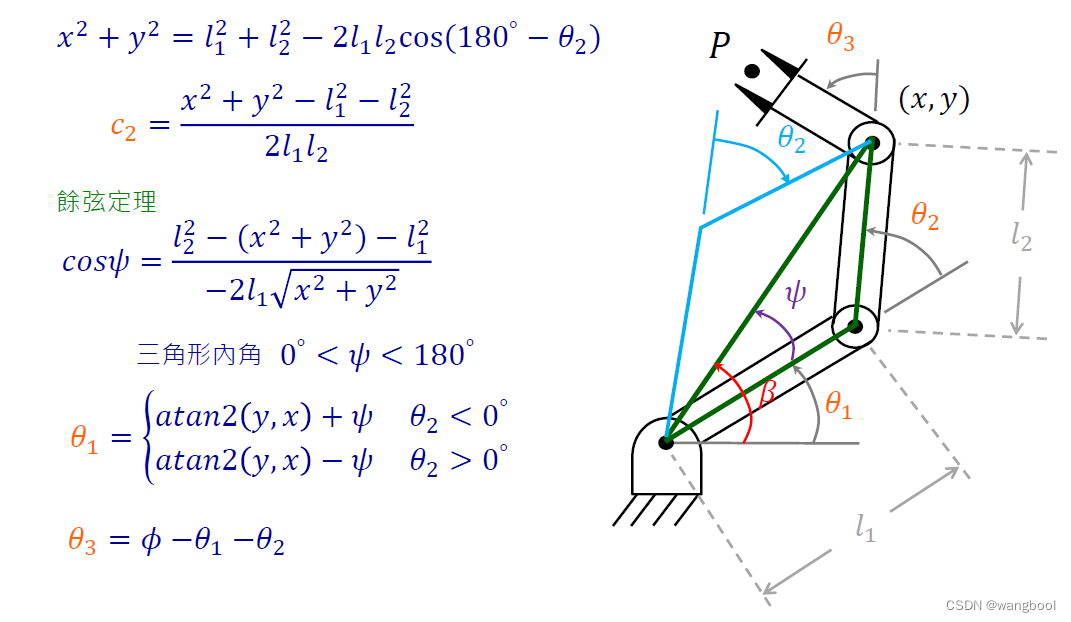
Ex:量化计算
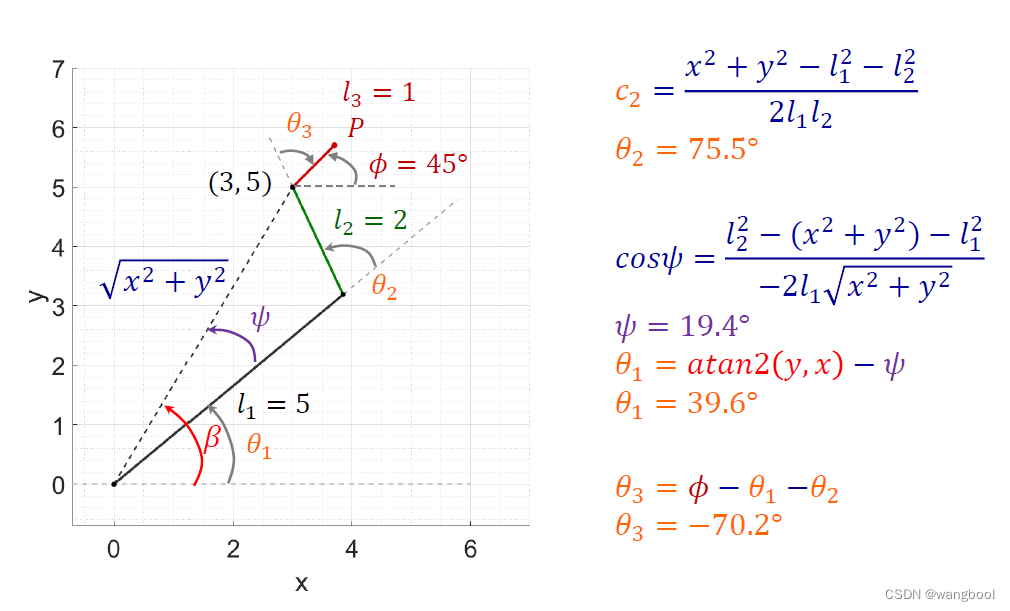
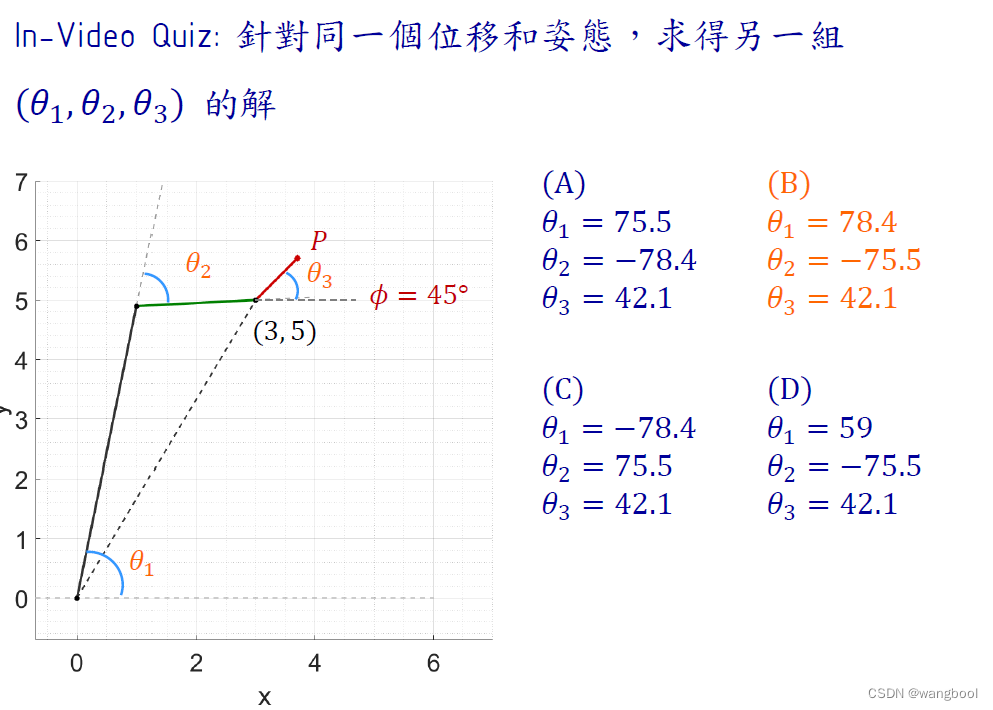
4.2.代数解


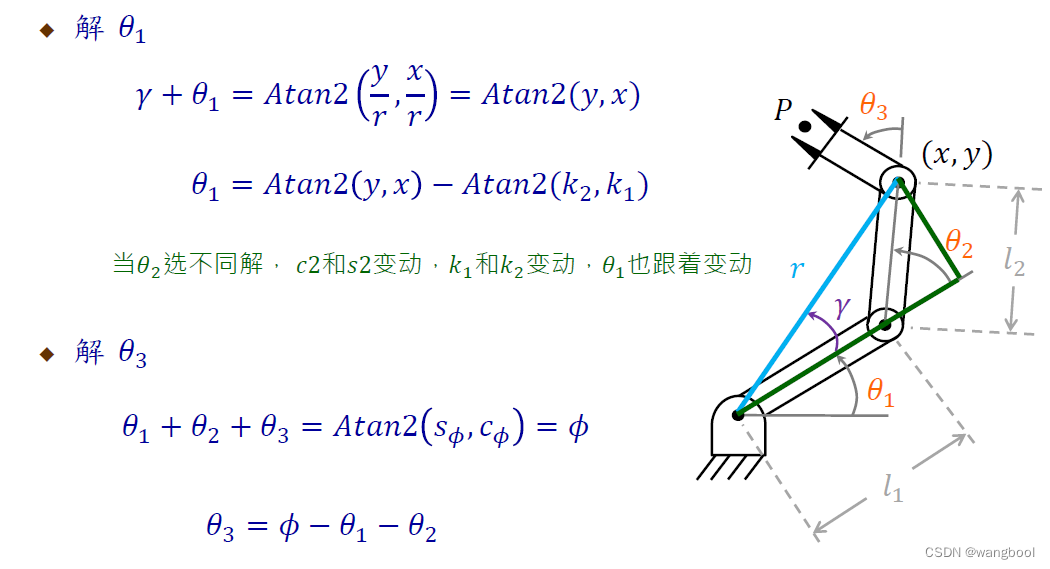
补充:三角函数方程式求解

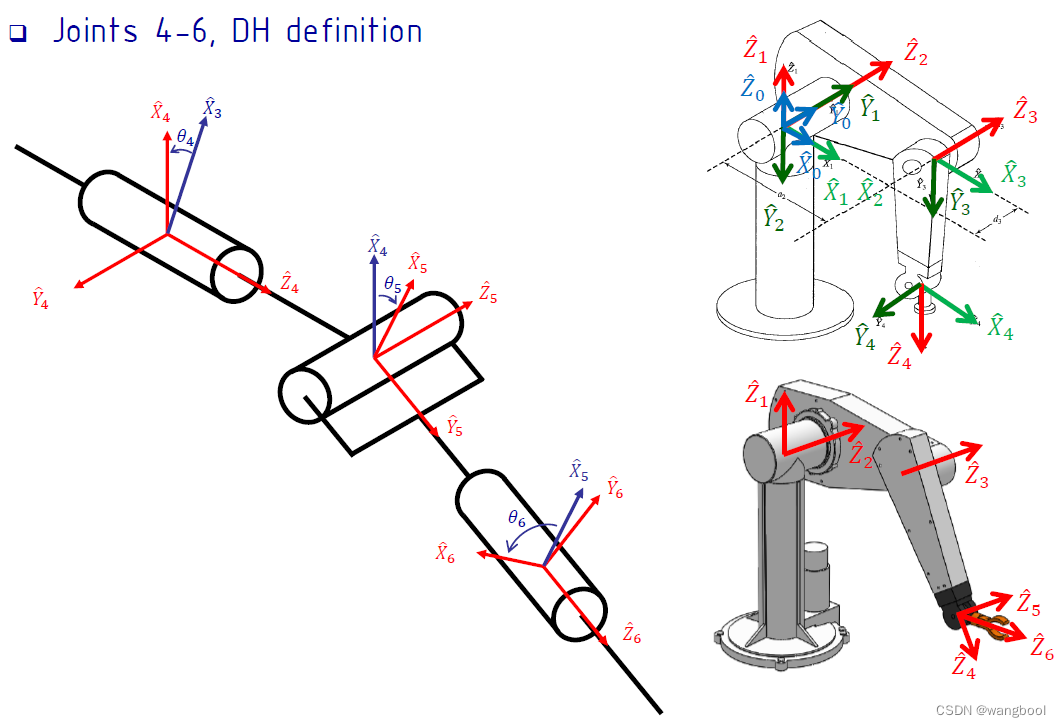
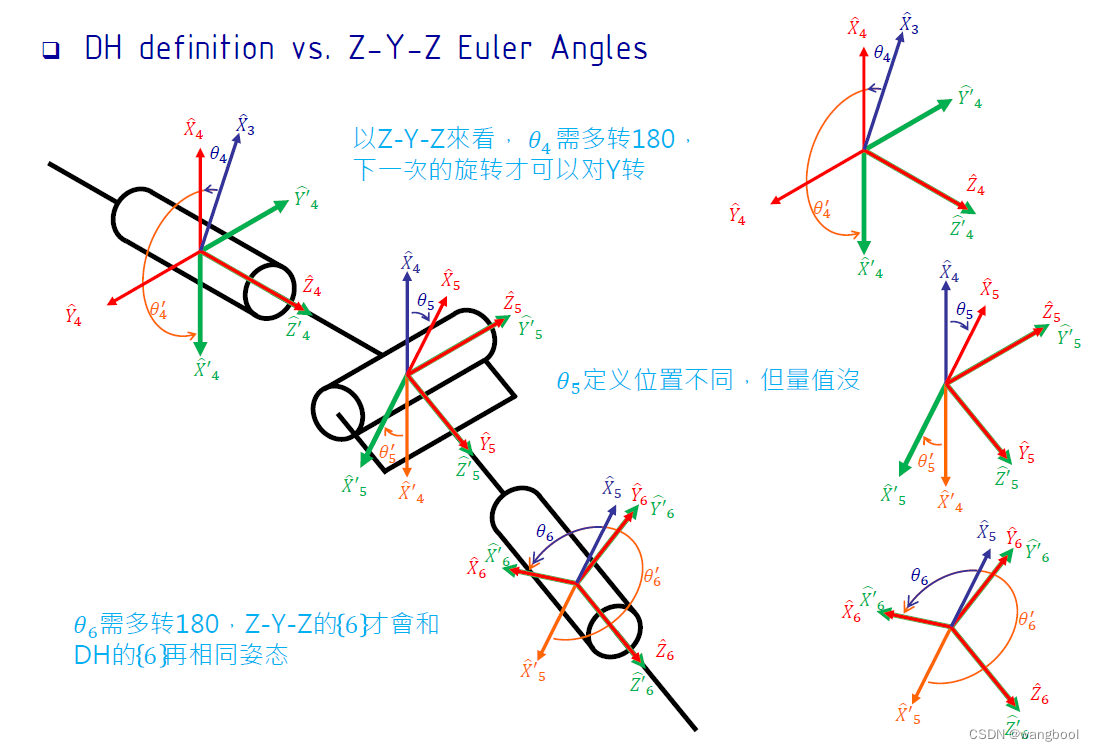
4.3. Pieper‘s solution
若6-DOF manipulator具有三个连续的轴交在同一点,则手臂有解析解。一般会把后三轴如此设计。
前三轴:产生移动
后三轴:产生转动
因为后三轴交在一点,即
0
P
6
O
R
G
=
0
P
4
O
R
G
^0P_{6~ORG} = ^0P_{4 ~ORG}
0P6 ORG=0P4 ORG
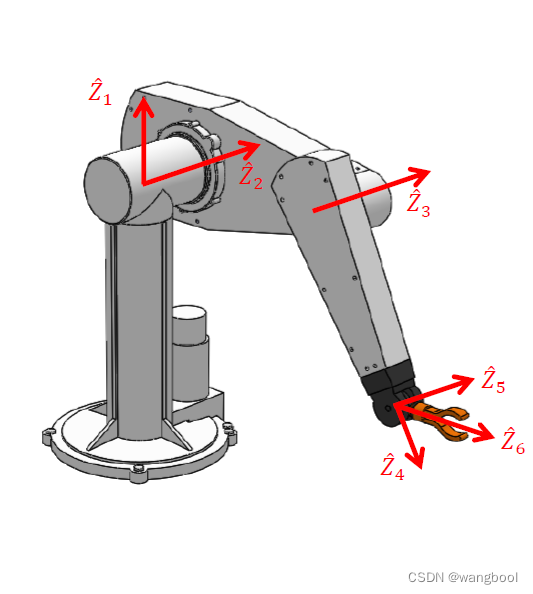
前三轴:移动


(
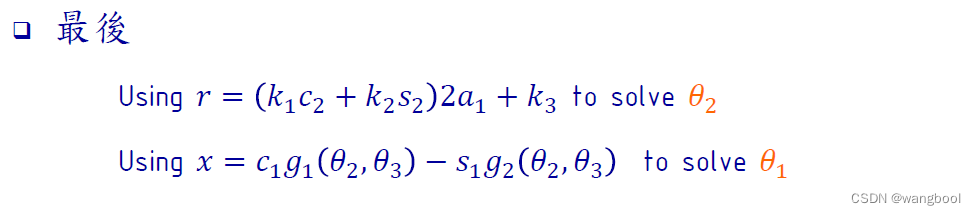
后三轴:转动

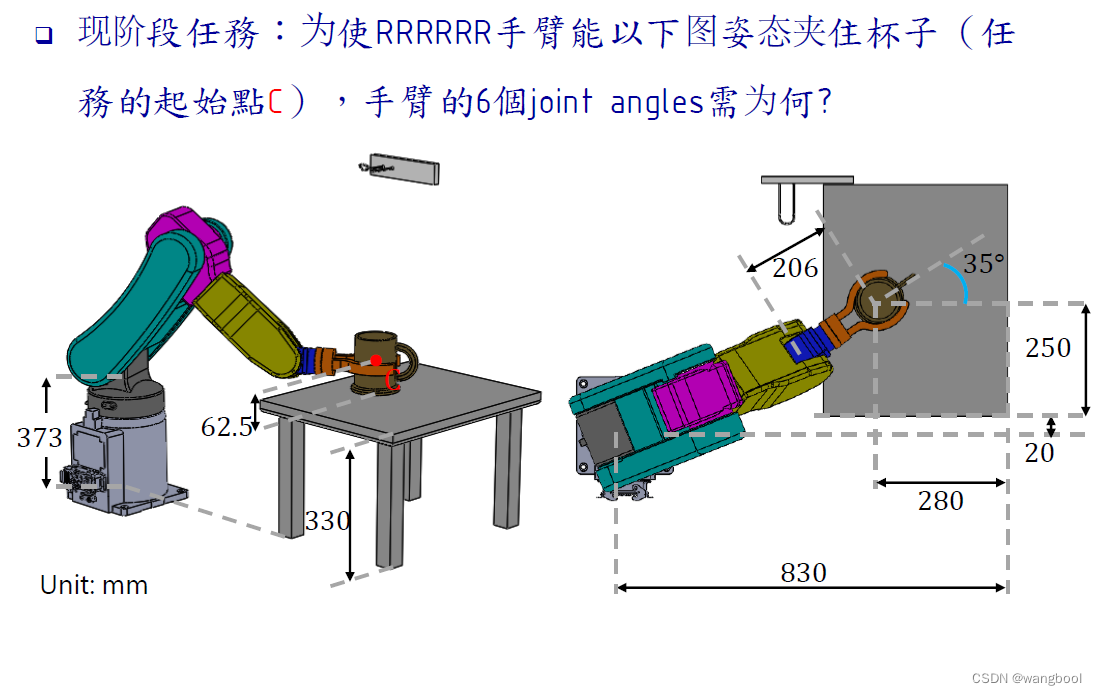
五、整个流程
情景:将一个杯子拿起来,然后将其挂在墙上,现在暂时只解决拿起来的问题