- 1推荐算法岗面试题收集_推荐算法面试题
- 2一年Java开发经验,阿里巴巴五面(已offer)面经,我自己都没有想到我会过_阿里巴巴java offer
- 3【PostgreSQL】导出数据库表(或序列)的结构和数据_pgsql导出表结构
- 4云监控(华为) | 实训学习day4(10)
- 5基于python-opencv学习系列——读取图像_python opencv读取图像
- 6Kafka知识总结(消费者+重平衡)
- 7Midjourney表情包制作及变现最全教程_mid journey制作表情包
- 8100页PPT云计算运营服务体系框架、应用体系、应用场景方案_云计算运营服务体系框架、应用体系、应用场景方案ppt
- 9我还是与他分手_xiao 77
- 10按照CIS-Tomcat7最新基线标准进行中间件层面基线检测_cis安全标准 tomcat
大数据分析与挖掘_大数据挖掘
赞
踩
第一章 绪论
大数据分析与挖掘简介
大数据的四个特点(4v):容量(Volume)、多样性(Variety)、速度(Velocity)和价值
概念:数据分析是用适当的统计分析方法,对收集来的大量数据进行分析,提取有用信息和形成结论并对数据加以详细研究和概括总结的过程。数据分析可以分为三个层次,即描述分析、预测分析和规范分析。
数据挖掘:是指从数据集合中提取人们感兴趣的知识,这些知识是隐含的、实现未知的、潜在有用的信息。提取出来的知识一般可表示为概念、规则、规律、模式等形式。
大数据分析与挖掘主要技术
大数据分析与挖掘的过程一般分为如下几个步骤:
- 任务目标的确定
这一步骤主要是进行应用的需求分析,特别是要明确分析的目标,了 解与应用有关的先验知识和应用的最终目标。 - 目标数据集的提取
这一步骤是要根据分析和挖掘的目标,从应用相关的所有数据中抽取数据集,并选择全部数据属性中与目标最相关的属性子集。 - 数据预处理
这一步聚用来提高数据挖掘过程中所需数据的质量,同时也能够提高挖掘的效率。数据预处理过程包括数据清洗、 数据转换、数据集成、数据约减等操作。 - 建立适当的数据分析与挖掘模型
这一步骤包含了大量的分析与挖掘功能,如统计分析、分类和回归、聚类分析、关联规则挖掘、异常检测等。 - 模型的解释与评估
这一步骤主要见对挖掘出的模型进行解释,可以用可视化的方式来展示它们以利于人们的理解。 对模型的评估可以采用自动或半自动方式来进行,目的是找出用户真正感兴趣或有用的模型。 - 知识的应用
将挖掘出的知识以及确立的模型部署在用户的应用中。但这并不代表数据挖掘过程的结束,还需要一个不断反馈和迭代的过程,使模型和挖掘出的知识更加完善。
数据挖掘主要包括如下的功能
- 对数据的统计分析与特征描述
- 关联规则挖掘和相关性性分析
- 分类和回归
例如决策树、贝叶斯分类器、KNN分类器、组合分类算法等,回归则是对数值型的函数进行建模,常用于数值预测。 - 聚类分析
聚类的主要目标是使聚类内数据的相似性最大,聚类间数据的相似性最小 - 异常检测
第二章 数据特征分析与预处理
数据类型
2.1.1数据集类型
- 结构化数据
即行数据,存储在数据库里,可以用二维表结构来逻辑表达实现的数据,所有的数据都具有相同的模式。 - 半结构化数据
半结构化数据也具有一定的结构,但是没有像关系数据库中那样严格的模式定义。
常见的半结构化数据主要有XML文档和JSON数据 - 非结构化数据
非结构化数据没有预定义的数据了模型,涵盖各种文档、文本、图片、报表、图像、音频、视频
数据属性的类型
- 标称属性
标称属性类似于标签,其中的数字或字符只是用来对物体进行识别和分类,不具有顺序关系,也不存在比较关系。
对标称属性不能做加减乘除运算,可以分析各个属性值出现的次数
当标称属性类别或状态数为两个的时候,称为二元属性,也被称为布尔属性,如果二元属性的两种状态具有相同的重要程度,则称为对称的。 - 序数属性
这种属性值之间可以有顺序关系,例如:学生成绩可以分为优秀、良好、中等、及格和不及格;产品质量可以分为优秀、合格和不合格。这样的属性称为序数属性,在统计学中也称为定序变量
标称、二元和序数属性的取值都是定性的,它们只描述对象的特征,如高、低等定性信息,并不给出实际的大小。可以用来比较大小,但还不能反应不同等级间的差异程度,不能进行加减乘除等数学运算 - 数值属性
数值属性是可以度量的,通常用实数来表示。
数值属性可以分为区间标度属性和比率标度属性。
(1)区间标度属性不能进行比率运算,例如20℃不能说是10℃的两倍,类似区间标度属性的还有日历日期、华氏温度、智商、用户满意度打分等。这些区间标度属性共同的特点是:用相等的单位尺度度量,属性的值有序,可以为正、负或零。相等的数字距离代表所测量相等的数量差值,在统计学上也称为定距变量。
(2)比率标度属性由于存在绝对零点,因此可以进行比率的计算,即它可进行加减乘除运算。这一类数值属性称为比率标度属性,在统计学中称为定比变量,是应用最广泛的一类数值属性
属性类型总结
| 标称属性 | 序数属性 | 区间标度属性 | 比率标度属性 | |
|---|---|---|---|---|
| 频数统计 | √ | √ | √ | √ |
| 众数 | √ | √ | √ | √ |
| 顺序关系 | √ | √ | √ | |
| 中位数 | √ | √ | √ | |
| 平均数 | √ | √ | ||
| 量化差异 | √ | √ | ||
| 加减运算 | √ | √ | ||
| 乘除运算 | √ | |||
| 定义"真正零值" | √ |
数据的描述性特征
描述数据几种趋势的度量
1. 算术平均数 一个包含n个数值型数据的集合,其算术平均数的定义是:x ˉ = 1 n ∑ i = 1 n x i \bar{x} = \frac{1}{n}\sum_{i=1}^{n}x_{i} xˉ=n1i=1∑nxi
(1)一个集合中的各个数据与算术平均数离差之和等于零,即:
∑
i
=
1
n
(
x
i
−
x
ˉ
)
=
0
\sum_{i=1}^{n}(x_{i}-\bar{x})=0
∑i=1n(xi−xˉ)=0 这个性质在数据的规范化中会被用到
(2)一个集合中的各个数据与算术平均数的离差平方之和是最小的。
算术平均数的缺点:容易受到集合中极端值或离群点的影响。
-
中位数
中位数是按照一定顺序排列后处于中间位置上的数据,中位数比算术平均数对于离群点的敏感度要低。当数据集合的分布呈现偏斜的时候,采用中位数作为集中趋势的度量更加有效 -
众数 (适合标称属性)
当数据的数量较大并且集中趋势比较明显的时候,众数更适合作为描述数据代表性水平的度量。 -
k百分位数
将一组数据从小到大排序,并计算相应的累计百分比,处于k%位置的值称为第k百分位数,用 X k % {X_{k\% }} Xk%表示。在一个集合里,有k%的数小于或等于 X k % {X_{k\% }} Xk%,有1-k%的数大于它。
例:设有一组数据:[-35,10,20,30,40,50,60,100],求它的25百分位数,即 X 25 % {X_{25\% }} X25%
一般有两种方法,分别是(n+1) * k%或者1+(n-1) * k%
X 25 % {X_{25\% }} X25%所在位置是1+(8-1)* 25%=2.75,处于第二个和第三个数之间,即10与20之间。如果采用线性插值的话 X 25 % {X_{25\% }} X25%=10+(20-10)* 0.75=17.5,中点:(10+20)/ 2=15 -
四分位数
四分位数是一种特殊的百分位数。
(1)第一四分位数Q1,又称“较小四分位数”,即25百分位数。
(2)第二四分位数Q2,就是中位数。
(3)第三四分位数Q3,又称“较大四分位数”,即75百分位数。
四分位数是比较常见的分析数据分布趋势的度量
描述数据离中趋势的度量
- 极差
极差是指一组数据中最大值与最小值之差,又称范围误差或全距,用R表示。 - 四位数极差(IQR)
四分位数极差也称内距,计算公式IQR=Q3-Q1,即第三四分位数减去第一四分位数的差,反应了数据集合中间50%数据的变动范围。
在探索性数据分析中,IQR可用于发现离群点,约翰·图基给了一个判定方法:超过Q3+1.5 * IQR或者低于Q1-1.5 * IQR的数据可能是离群点。
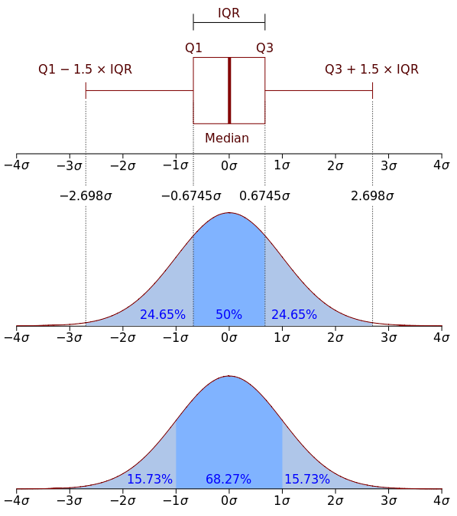
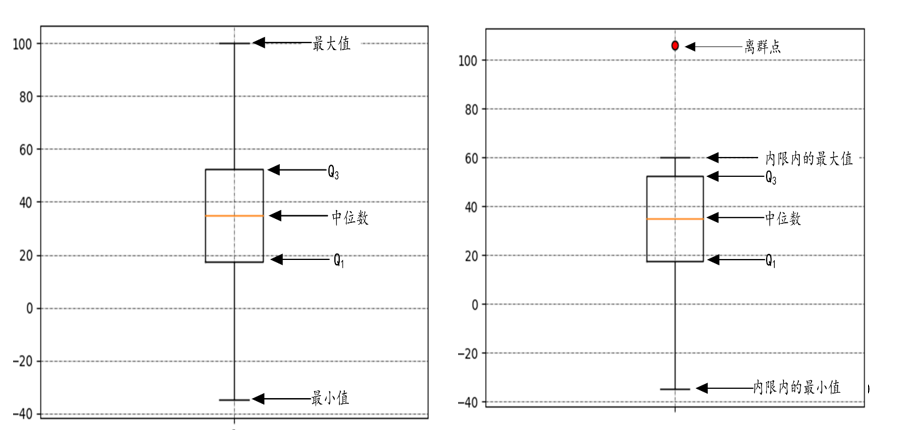
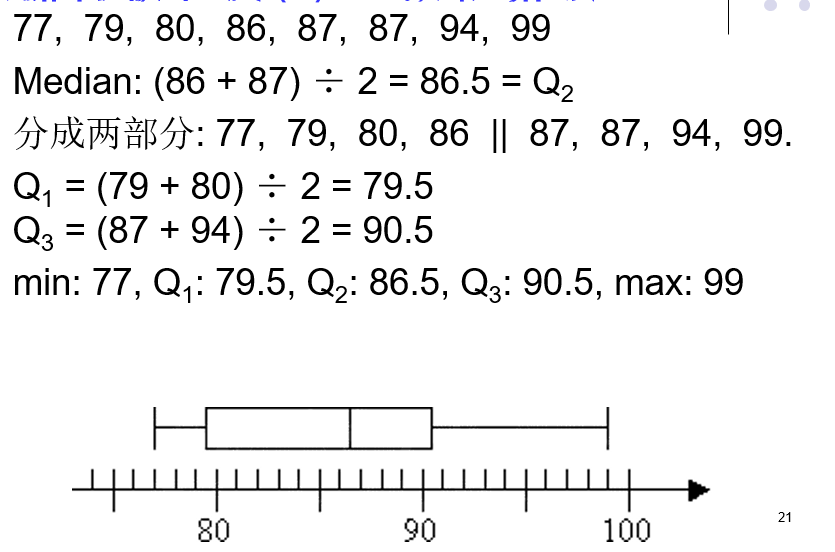
- 平均绝对离差
计算数据结合中各个数值与平均值的距离综合,然后取其平均数。
M A D = 1 n ∑ i = 1 n ∣ x i − x ˉ ∣ MAD=\frac{1}{n}\sum_{i=1}^{n}|x_{i}-\bar{x}| MAD=n1i=1∑n∣xi−xˉ∣
- 方差和标准差
♦样本方差的计算公式:
总体的方差:
σ 2 = ∑ ( X − μ ) 2 N {\sigma ^2}{\rm{ = }}\frac{{\sum {{{(X - \mu )}^2}} }}{N} σ2=N∑(X−μ)2
样本方差:
s 2 = 1 n − 1 ∑ i = 1 n ( x i − x ‾ ) 2 {s^2}{\rm{ = }}\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{({x_i} - \overline x )}^2}} s2=n−11i=1∑n(xi−x)2
♦标准差
标准差=方差的算数平方根
5. 离散系数
离散系数又称变异系数,样本变异系数是样本标准差与样本平均数之比:
C
v
=
s
x
−
{{\rm{C}}_{\rm{v}}} = \frac{s}{{\mathop x\limits^ - }}
Cv=x−s
数据分布形态的度量
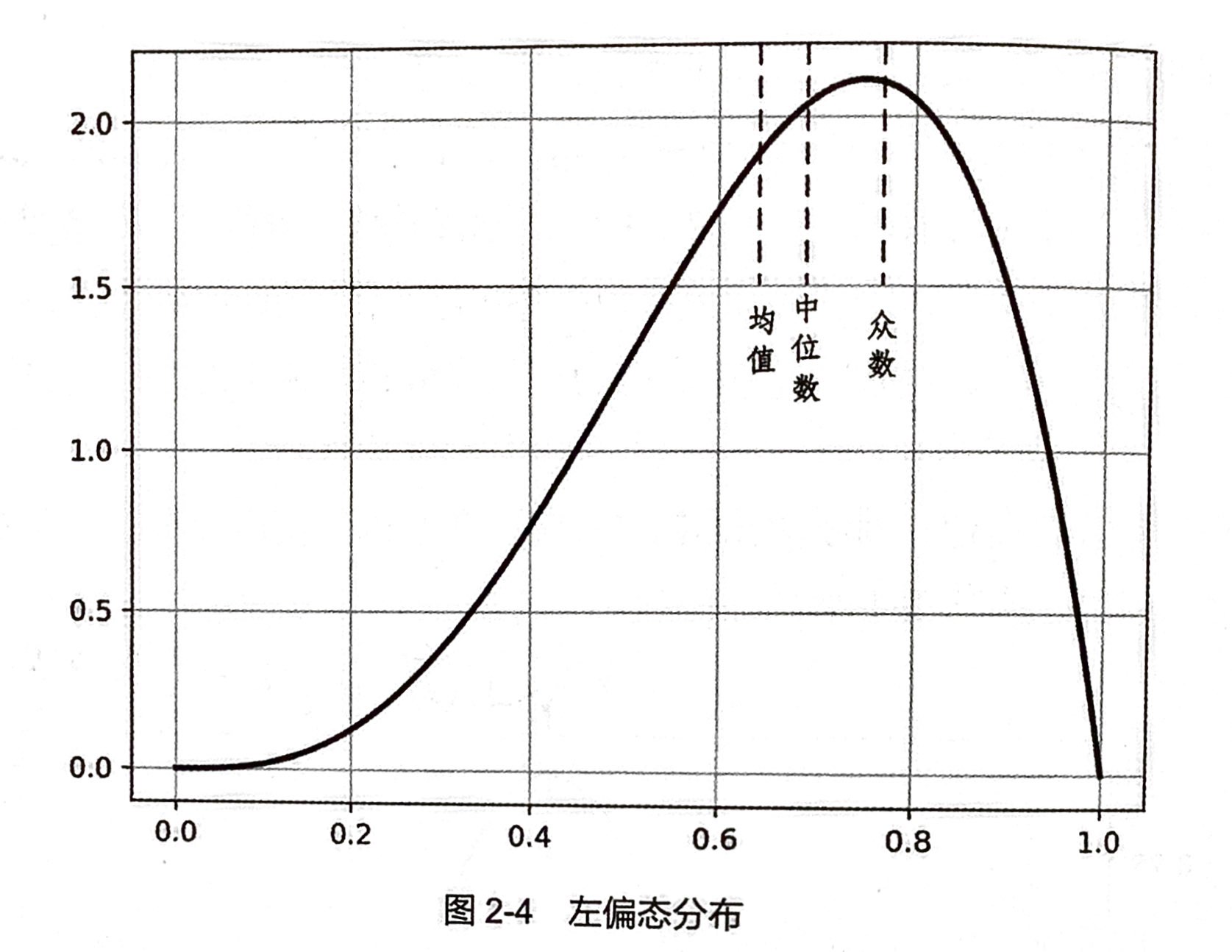
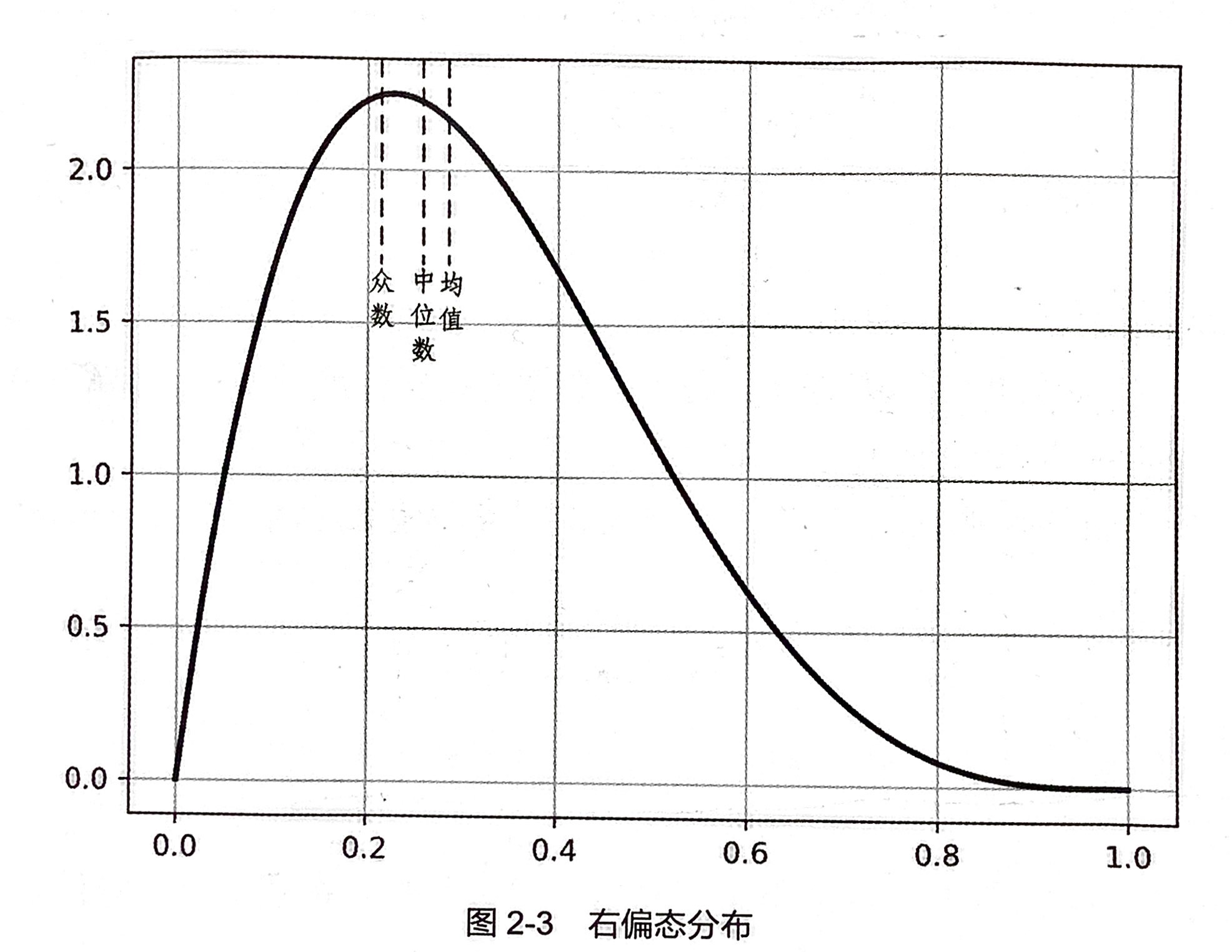
皮尔逊偏态系数
s
k
1
=
x
−
−
M
0
s
s{k_1} = \frac{{\mathop x\limits^ - - {M_0}}}{s}
sk1=sx−−M0 或者
s
k
2
=
3
(
x
−
−
M
d
)
s
s{k_2} = \frac{{3(\mathop x\limits^ - - {M_d})}}{s}
sk2=s3(x−−Md)
其中,$\mathop x\limits^ - \$ 是平均数,$\{M_0}\
是重数,
是重数,
是重数,\{M_d}\$是中位数,s是样本标准差
数据的峰度及度量
峰度用于衡量数据分布的平坦度,它以标准正态分布作为比较的基准。峰度的度量使用峰度系数:
k = 1 n ∑ i = 1 n ( x i − x ˉ ) 4 ( 1 n ∑ i = 1 n ( x i − x ˉ ) ) 2 − 3 k = \frac{\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x})^{4}}{(\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x}))^{2}}-3 k=(n1∑i=1n(xi−xˉ))2n1∑i=1n(xi−xˉ)4−3
k≈0,称为常峰态,接近于正态分布。
k<0,称为低峰态。
k>0,称为尖峰态。
数据偏度和峰度的作用
给定一个数据集合,通过计算它的偏度和峰度,可以符集数据分布与正态分布的差异,结合前面介绍的数据集中和离中趋势度量,就能够大致判断数据分布的形状等概要性信息,增加对数据的理解程度。
箱型图
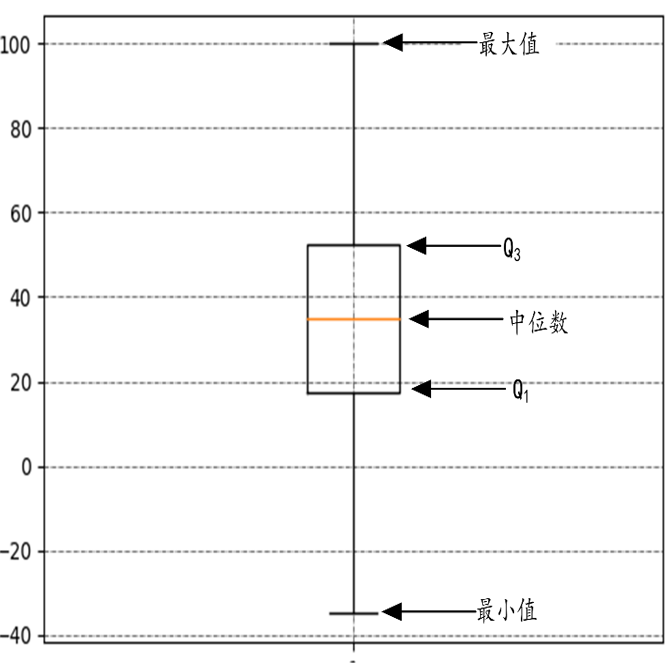
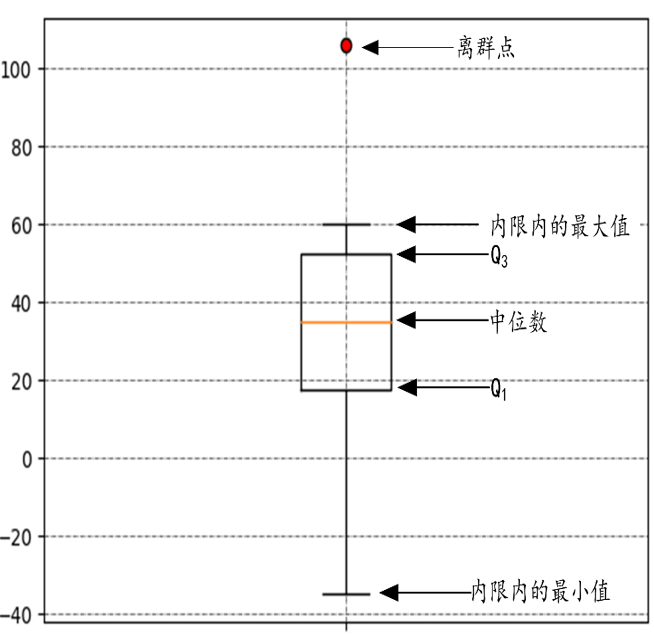
数据的相关分析
相关分析
-
散点图
判断两个属性之间是否有相关性,可以首先通过散点图进行直观判断。
散点图是将两个属性的成对数据,绘制在直角坐标系中得到的一系列点,可以直观地描述属性间是否相关、相关的表现形式以及相关的密切程度。
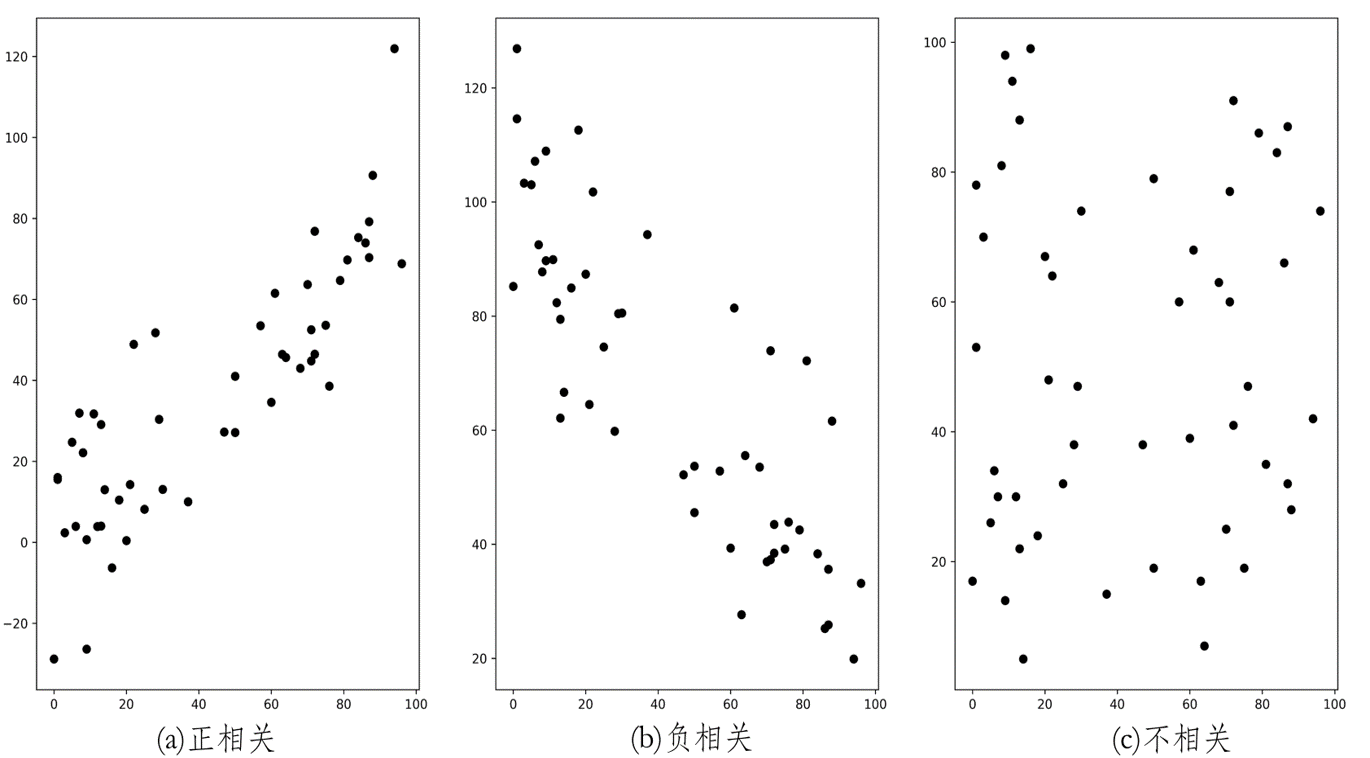
-
相关系数
数据的各个属性之间关系密切程度的度量,主要是通过相关系数的计算与检验来完成的。
属性X和Y之间的样本协方差的计算公式:
c o v ( X , Y ) = ∑ i = 1 n ( X i − X − ) ( Y i − Y − ) n − 1 {\mathop{\rm cov}} (X,Y) = \frac{{\sum\limits_{i = 1}^n {({X_i} - \mathop X\limits^ - )({Y_i} - \mathop Y\limits^ - )} }}{{n - 1}} cov(X,Y)=n−1i=1∑n(Xi−X−)(Yi−Y−)
协方差的正负代表两个属性相关性的方向,而协方差的绝对值代表它们之间关系的强弱。 -
样本相关系数,协方差的大小与属性的取值范围、量纲都有关系,构成不同的属性对之间的协方差难以进行横向比较。为了解决这个问题,把协方差归一化,就得到样本相关系数的计算公式:
$$\r(X,Y) = \frac{{{\mathop{\rm cov}} (X,Y)}}{{{s_X}{s_Y}}}\$$
$\{s_X}{s_Y}\$标准差
相关系数消除了两个属性量纲的影响,它是无量纲的。相关系数的取值范围:-1<=r<=1;若0<r<=1,表示X和Y之间存在正线性相关关系;若-1<=r<0,表明X和Y之间存在负线性相关关系。若r=0,说明两者之间不存在线性相关关系,但并不排除两者之间存在非线性关系。
卡方检验
可以用相关系数来分析两个数值型属性之间的相关性。对于两个标称属性(分类属性),他们之间的独立性检验可以使用卡方检验来推断。
χ
2
=
∑
(
O
b
s
e
r
v
e
d
−
E
x
p
e
c
t
e
d
)
2
E
x
p
e
c
t
e
d
{\chi ^2} = \sum {\frac{{{{(Observed - Expected)}^2}}}{{Expected}}}
χ2=∑Expected(Observed−Expected)2
| 男 | 女 | 合计 | |
|---|---|---|---|
| 小说 | 250(90) | 200(360) | 450 |
| 非小说 | 50(210) | 1000(840) | 1050 |
| 合计 | 300 | 1200 | 1500 |
| χ 2 {\chi ^2} χ2=507.93 | |||
| 自由度 dof=(r-1)(c-1) r和c分别是两个属性各个分类值的个数 | |||
| 自由度=(2-1)(2-1) | |||
| χ 2 {\chi ^2} χ2就是统计样本的实际观测值与理论推算值之间的偏离程度。Observed(观测),Expected(理论) |
数据预处理
定义:对原始数据进行必要的清洗、集成、转换和归约等一系列处理,使数据达到进行只是获取所要求的规范和标准零均值化
将每一个属性的数据都减去这个属性的均值后,形成一个新数据集合,变换后各属性的数据之和与均值都为零。各属性的方差不发生变化,各属性间的协方差也不发生变化。
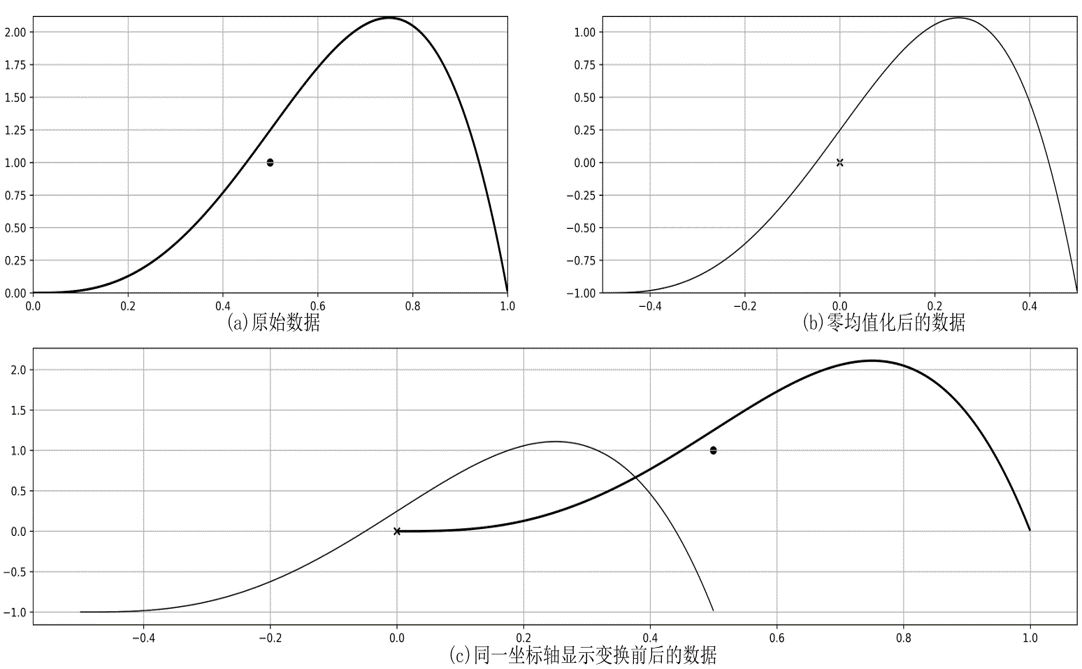
z分数变换
标准分数也叫z分数,用公式表示为:
z
=
x
−
x
−
s
z = \frac{{x - \mathop x\limits^ - }}{s}
z=sx−x−
其中x为原始数据, $\mathop x\limits^ - \$为样本均值,s为样本标准差。变换后数据的均值为0,方差为1。无量纲,数据尽量满足高斯分布。
z值表示袁术数据和样本均值之间的距离,是以标准差为单位计算的。原始数据低于标准值时,z为负数,反之为正数。
**缺点:**假如原始数据并没有呈高斯分布,标准化的数据分布效果不好
最小-最大规范化
最小-最大规范化又称离差标准化,是对原始数据的线性转换,将数据按照比例缩放至一个特定区间。假设原来数据分布在区间[min,max],要变换到区间[min’,max’],公式如下:
v ′ = m i n ′ + v − m i n m a x − m i n ( m a x ′ − m i n ′ ) v^{'}=min^{'}+\frac{v-min}{max-min}(max^{'}-min^{'}) v′=min′+max−minv−min(max′−min′)
独热编码
独热编码又称一位有效编码,用来对标称属性(分类属性)进行编码。
例,产品的颜色有{黑、白、蓝、黄}四种取值,分别用1、2、3、4来编码,假设有5个产品如下所示:
| ID | 颜色 |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
问题:各个不同颜色值之间没有顺序关系,但从上述编码来看,颜色黑和黄之间的差异为3,而蓝和黄差异为1,似乎黄色和蓝色更相似一些。因此,按照这种简单的编码方式计算对象之间的差异时,就会得到错误的结果。
在上面的例子中,可以将一个颜色标称属性扩充为4个二元属性,分别对应黑、白、蓝、黄四种取值。对于每一个产品,它在这四个属性上只能有一个取1,其余三个都为0,所以称为独热编码
| ID | 黑色 | 白色 | 蓝色 | 黄色 |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 1 |
| 任意两个不同颜色的产品之间的欧氏距离都是: | ||||
| ( 1 − 0 ) 2 + ( 0 − 1 ) 2 + ( 0 − 0 ) 2 + ( 0 − 0 ) 2 = 2 \sqrt{(1-0)^{2}+(0-1)^{2}+(0-0)^{2}+(0-0)^{2}}=\sqrt{2} (1−0)2+(0−1)2+(0−0)2+(0−0)2 =2 | ||||
| 可以看出,每一个标称属性扩充为独热编码后,在每一组新属性中,只有一个为1,其余同组的扩充属性值都为0,这就造成独热编码构成的向量较稀疏。 | ||||
| 独热编码能够处理非连续性数值属性,并在一定程度上扩充了数值的特征(属性)。如在上例中颜色本身只是一个特征,经过独热编码以后,扩充成了四个特征。 | ||||
| 使用独热编码,将离散属性的取值扩展到欧氏空间,回归、分类、聚类等很多数据挖掘算法对距离或相似度的计算是非常普遍的,而独热编码会让距离的计算更加合理。 | ||||
| 在实际应用独热编码时,要注意它的引入有时会带来数据属性(维数)极大扩张的负面影响。 |
数据抽样技术
不放回简单随机抽样
例:设有一组数据: [11,13,16, 19,27, 36,43, 54, 62, 75], 现在想要从中不放回随机抽样5个数据,每个数据被抽中的概率分别为[0.1, 0.05, 0.05, 0.05, 0.05, 0.1, 0.1,0.1,0.1, 0.3]。
抽样过程如下。
(1 )根据待抽样数据的概率,计算以数组形式表示的累计分布概率edf,并规范化。
计算: cdf=[0.1,0.15,0.2,0.25,0.3, 0.4, 0.5, 0.6,0.7, 1]
规范化: cdf/=cdf[-1], 得到:[0.1,0.15,0.2,0.25, 0.3, 0.4, 0.5,0.6,0.7,1]
(2)根据还需抽样的个数,生成[0,1]的随机数数组x。
[0.04504848, 0.5299489, 0.0734825, 0.52341745, 0.17316974]
(3)将x中的随机数按照cdf值升序找到插入位置,形成索弓数组new。
[0,7,0,7,2]
(4)找出数组new中不重复的索引位置,作为本次抽样的位置索引。
[0 7 2]
(5)在概率数组p中,将已经抽样的索引位置置0。
P=[0, 0.05, 0., 0.05, 0.05, 0.1, 0.1, 0., 0.1, 0.3]
(6)重复上述步骤,知道输出指定数目的样本
水库抽样
输入:一组数据,其大小未知
输出:这组数据的K个均匀抽样
要求:
- 仅扫描数据一次
- 空间复杂性为O(K)【和抽样大小有关,和整个数据量无关,不可把所有数据都放在内存里进行抽样】
- 扫描到数据的前n个数字时(n>K),保存当前已扫描数据的K个均匀抽样
针对此种需求,水库抽样法应运而生
算法步骤:
- 申请一个长度为K的数组A保存抽样
- 保存首先接收到的K个元素
- 当接收到第 i 个新元素 t 时,以 K / i 的概率随机替换A中的元素(即生成 [ 1, i ]间随机数j,若 j ≤ K,则以 t 替换 A[ j ])
算法性质:
- 该采样是均匀的。
即在任何时候,接收到的大于K的n个数据,选出来的数都保证是均匀采样。
证明:
- 假设(n-1)次采样后, 缓冲区中k个样本的采样概率为声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/正经夜光杯/article/detail/855161
Copyright © 2003-2013 www.wpsshop.cn 版权所有,并保留所有权利。


