社交网络分析——信息传播模型（附带三个模型的python实现）

摘要：主要讲解一些基本的信息传播模型，以及IC模型、SI模型和SIR模型的python实现及可视化。

• 2021.10.06更新
• 有需要的可以点击传送门

• 2020.09.26更新
• 更新了SIR模型的实现，请点击传送门，就不放在这篇博客里了

• 2020.09.03更新
• 更新了SI模型和IC模型用不同颜色表示每次激活的节点，在本文最后

author：xiao黄
缓慢而坚定的生长

信息传播模型

影响力模型

• IC模型
• LT模型

传染模型

• SI模型
• SIR模型
• SIS模型
• SIRS模型

Influence Models

• 影响模型可模拟用户如何影响网络中的每个人
• 节点有两个状态
  未激活：节点未收到信息
  激活：节点收到信息并且能够传播给他们的邻居

Independent Cascade (IC) Model

• 在 t 时刻被激活的节点在 t+1 时刻仅有一次机会去激活其邻居
• 假设节点 v 在 t 时刻被激活，对于 v 的任何邻居 w ，w 在 t+1 时刻被激活的概率是$Pvw$
• 如果是无权重的话，可以都设置为0.5，那么这样传播与不传播的概率就是一半一半了
  

例子

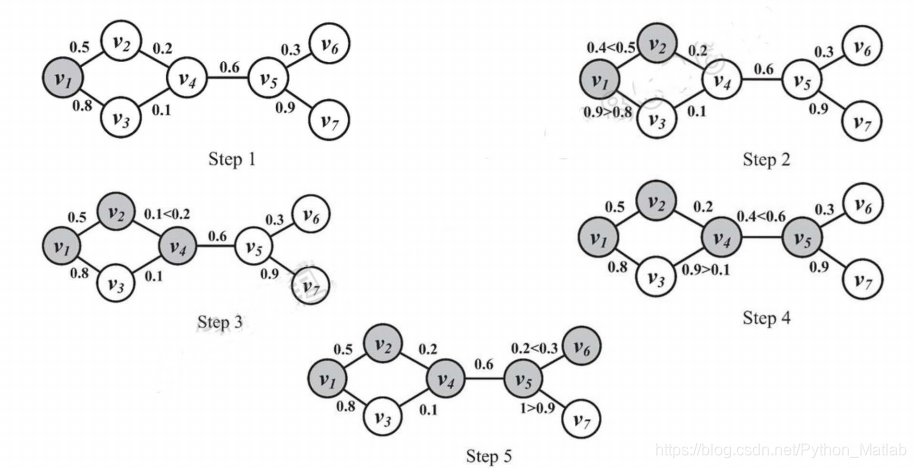
Liner Threshold (LT) Model

• 在任意时刻，激活的点都可以影响未被激活的点
• 每个节点都有激活阈值
• 如果影响程度超过该节点的阈值，则这节点被激活

Infection Models

• 传染模型也叫流行病模型，用于描述个人传播传染病的方式
• 节点有两种状态
  易感人群：易感节点可能会感染疾病
  感染人群：感染节点有机会去感染易感人群
  免疫人群：感染节点被治愈后不会再得疾病的人群

Susceptible Infected (SI) Model

• 节点有两个状态
  易感节点（S）
  感染节点（I）
• 如何传染
  一个节点被感染，它将持续传染周围的节点
  在每个离散时间中，每个被感染的节点尝试以概率p去感染它的易感（未感染）邻居
  

Susceptible Infected Recovered (SIR) Model

• Intuition:一些被感染的节点以一定的概率成为免疫节点，免疫节点不能被感染疾病或者传播疾病
• 节点有三种状态：
  易感节点；感染节点；免疫节点
• 节点的变化
  
  β：易感节点被成功感染的概率
  γ：感染节点被治愈的概率

Susceptible Infected Susceptible (SIS) Model

• Intuition：感染节点以一定的概率变成易感节点，又有一定的概率被感染成感染节点
• 节点有两种状态
  易感节点；感染节点
• 节点的变化
  
  β：易感节点被成功感染的概率
  γ：感染节点被治愈成易感节点的概率

Susceptible Infected Recovered Susceptible (SIRS) Model

• Intuition：免疫节点有一定的概率变成易感节点
• 节点的变化
  
  β：易感节点被成功感染的概率
  γ：感染节点被治愈成免疫节点的概率
  λ：免疫节点有一定的概率转化成易感节点

IC模型的python实现

先上代码，这里我就不解释了，代码里面的注释我觉得很详细了，不懂可以评论或者私信。

import random

import matplotlib.pyplot as plt
import networkx as nx
import numpy as np

max_iter_num = 10 # 模拟的次数
G = nx.karate_club_graph() # 空手道俱乐部

for edge in G.edges:
    G.add_edge(edge[0], edge[1], weight=random.uniform(0,1)) # 可不可以作为权值
for node in G:
    G.add_node(node, state = 0) # 用state标识状态 state=0 未激活，state=1 激活

seed = 33 # 选定33作为初始激活节点
G.node[seed]['state'] = 1 # 表示33被激活

activated_graph = nx.Graph() # 被激活的图
activated_graph.add_node(seed)

all_active_nodes = [] # 所有被激活的节点放在这里
all_active_nodes.append(seed)

start_influence_nodes = [] # 刚被激活的节点 即有影响力去影响别人的节点
start_influence_nodes.append(seed)

for i in range(max_iter_num):
    new_active = list()
    t1 = '%s time' % i + ' %s nodes' % len(all_active_nodes)
    print(t1) # 当前有多少个节点激活

    # 画图
    plt.title(t1)
    nx.draw(activated_graph, with_labels=True)
    plt.show()

    for v in start_influence_nodes:
        for nbr in G.neighbors(v): 
            if G.node[nbr]['state'] == 0: # 如果这个邻居没被激活
                edge_data = G.get_edge_data(v, nbr)
                if random.uniform(0, 1) < edge_data['weight']:
                    G.node[nbr]['state'] = 1
                    new_active.append(nbr)
                    activated_graph.add_edge(v, nbr) # 画图 添加边
    
    start_influence_nodes.clear() # 将原先的有个影响力的清空
    start_influence_nodes.extend(new_active) # 将新被激活的节点添加到有影响力
    all_active_nodes.extend(new_active) # 将新被激活的节点添加到激活的列表中
    print('all_active_nodes',all_active_nodes) # 打印
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

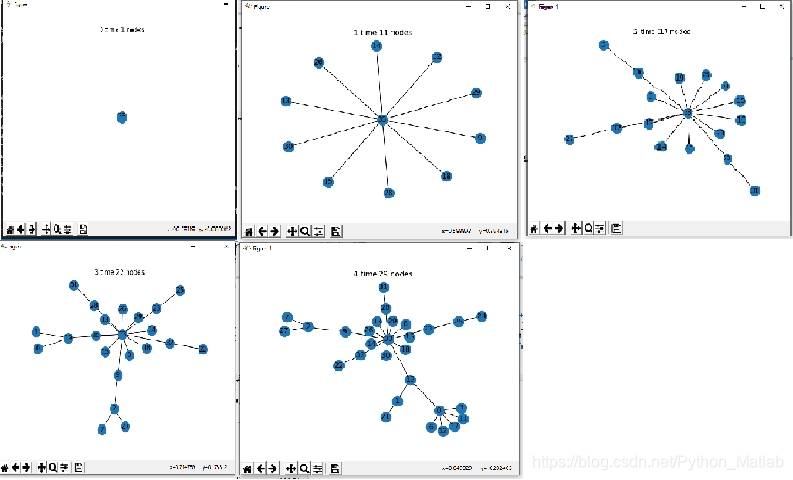
程序运行结果图：

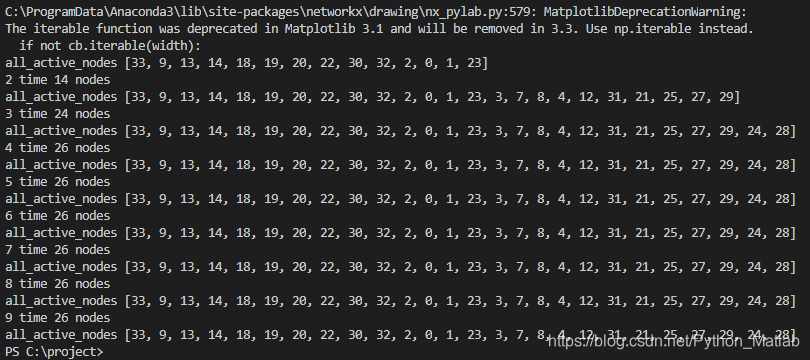
节点图，这里我就放了9张，第十张不放了，你们运行的时候会看到的

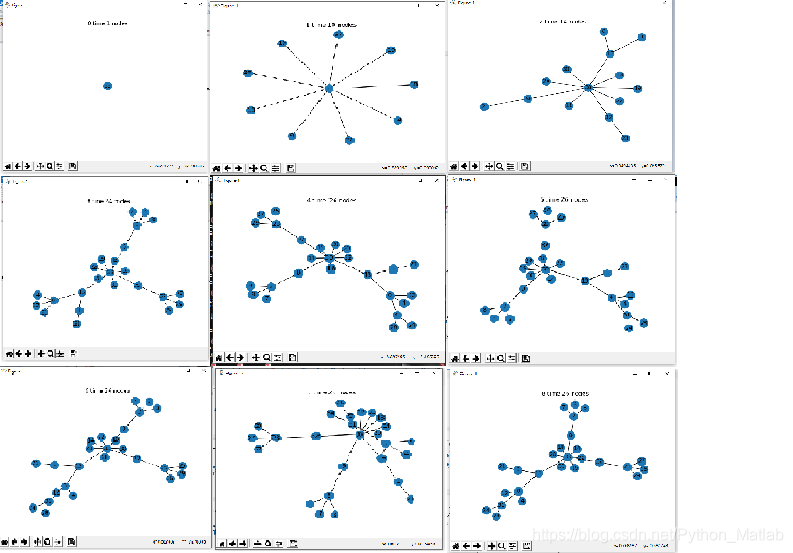
SI模型的python实现

先上代码，这里我就不解释了，代码里面的注释我觉得很详细了，不懂可以评论或者私信。

import random

import matplotlib.pyplot as plt
import networkx as nx
import numpy as np

max_iter_num = 5 # 模拟的次数
G = nx.karate_club_graph() # 空手道俱乐部

for edge in G.edges:
    G.add_edge(edge[0], edge[1], weight=random.uniform(0,1)) # 可不可以作为权值 病毒的感染能力
for node in G:
    G.add_node(node, state = 0) # 用state标识状态 state=0 未激活，state=1 激活

seed = 33 # 选定33作为传染源
G.node[seed]['state'] = 1 # 表示33是感染的

all_infect_nodes = [] # 所有被感染的节点放在这里
all_infect_nodes.append(seed)

infected_graph = nx.Graph() # 被激活的图
infected_graph.add_node(seed)

for i in range(max_iter_num):
    new_infect = list() # 新被感染的
    t1 = '%s time' % i + ' %s nodes' % len(all_infect_nodes)
    print(t1) # 当前有多少个节点被感染
    
    # 画图
    plt.title(t1)
    nx.draw(infected_graph, with_labels=True)
    plt.show()

    # 感染的机会不止一次
    for v in all_infect_nodes:
        for nbr in G.neighbors(v):
            if G.node[nbr]['state'] == 0: # 如果这个邻居节点没被感染
                edge_data = G.get_edge_data(v, nbr)
                if random.uniform(0, 1) < edge_data['weight']:
                    G.node[nbr]['state'] = 1
                    new_infect.append(nbr)
                    infected_graph.add_edge(v, nbr) # 画图 添加边
    
    all_infect_nodes.extend(new_infect) # 将新感染的添加到
    print('all_active_nodes:', all_infect_nodes)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

运行结果：

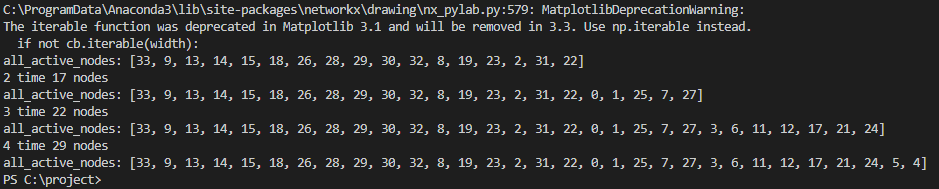
节点效果图：

IC模型的python实现更新版（2020.09.03）

import random

import matplotlib.pyplot as plt
import networkx as nx
import numpy as np

max_iter_num = 10 # 模拟的次数
G = nx.karate_club_graph() # 空手道俱乐部

for edge in G.edges:
    G.add_edge(edge[0], edge[1], weight=random.uniform(0,1)) # 可不可以作为权值
for node in G:
    G.add_node(node, state = 0) # 用state标识状态 state=0 未激活，state=1 激活

seed = 33 # 选定33作为初始激活节点
G.node[seed]['state'] = 1 # 表示33被激活

# activated_graph = nx.Graph() # 被激活的图
# activated_graph.add_node(seed)

all_active_nodes = [] # 所有被激活的节点放在这里
all_active_nodes.append(seed)

start_influence_nodes = [] # 刚被激活的节点 即有影响力去影响别人的节点
start_influence_nodes.append(seed)

color_list = ['brown','orange','r','g','b','y','m','gray','black','c','pink','brown','orange','r','g','b','y','m','gray','black','c','pink']
res = [[seed]]
for i in range(max_iter_num):
    new_active = list()
    t1 = '%s time' % i + ' %s nodes' % len(all_active_nodes)
    print(t1) # 当前有多少个节点激活

    # 画图
    # plt.title(t1)
    # nx.draw(activated_graph, with_labels=True,node_color=color_list[i])
    # plt.show()

    for v in start_influence_nodes:
        for nbr in G.neighbors(v): 
            if G.node[nbr]['state'] == 0: # 如果这个邻居没被激活
                edge_data = G.get_edge_data(v, nbr)
                if random.uniform(0, 1) < edge_data['weight']:
                    G.node[nbr]['state'] = 1
                    new_active.append(nbr)
                    # activated_graph.add_edge(v, nbr) # 画图 添加边
    
    print('激活',new_active)
    start_influence_nodes.clear() # 将原先的有个影响力的清空
    start_influence_nodes.extend(new_active) # 将新被激活的节点添加到有影响力
    all_active_nodes.extend(new_active) # 将新被激活的节点添加到激活的列表中
    res.append(new_active)

    print('all_active_nodes',all_active_nodes) # 打印
# print(res)

res = [c for c in res if c]
pos = nx.spring_layout(G) # 节点的布局为spring型
nx.draw(G,pos, with_labels=True, node_color='w', node_shape = '.')
color_list = ['brown','orange','r','g','b','y','m','gray','black','c','pink','brown','orange','r','g','b','y','m','gray','black','c','pink']
for i in range(len(res)):
    nx.draw_networkx_nodes(G, pos, with_labels=True, node_color=color_list[i], nodelist=res[i])
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

结果图：

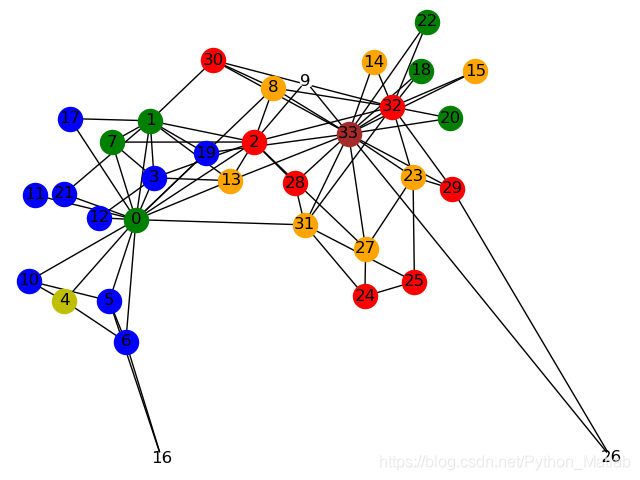
SI模型的python实现更新版（2020.09.03）

import random

import matplotlib.pyplot as plt
import networkx as nx
import numpy as np

max_iter_num = 5 # 模拟的次数
G = nx.karate_club_graph() # 空手道俱乐部

for edge in G.edges:
    G.add_edge(edge[0], edge[1], weight=random.uniform(0,1)) # 可不可以作为权值 病毒的感染能力
for node in G:
    G.add_node(node, state = 0) # 用state标识状态 state=0 未感染，state=1 激活

seed = 33 # 选定33作为传染源
G.node[seed]['state'] = 1 # 表示33是感染的

all_infect_nodes = [] # 所有被感染的节点放在这里
all_infect_nodes.append(seed)
res = [[seed]]

# infected_graph = nx.Graph() # 被激活的图
# infected_graph.add_node(seed)

for i in range(max_iter_num):
    new_infect = list() # 新被感染的
    t1 = '%s time' % i + ' %s nodes' % len(all_infect_nodes)
    print(t1) # 当前有多少个节点被感染
    
    # 画图
    # plt.title(t1)
    # nx.draw(infected_graph, with_labels=True)
    # plt.show()

    # 感染的机会不止一次
    for v in all_infect_nodes:
        for nbr in G.neighbors(v):
            if G.node[nbr]['state'] == 0: # 如果这个邻居节点没被感染
                edge_data = G.get_edge_data(v, nbr)
                if random.uniform(0, 1) < edge_data['weight']:
                    G.node[nbr]['state'] = 1
                    new_infect.append(nbr)
                    # infected_graph.add_edge(v, nbr) # 画图 添加边
    res.append(new_infect)
    all_infect_nodes.extend(new_infect) # 将新感染的添加到
    print('all_active_nodes:', all_infect_nodes)

res = [c for c in res if c]
pos = nx.spring_layout(G) # 节点的布局为spring型
nx.draw(G,pos, with_labels=True, node_color='w', node_shape = '.')
color_list = ['brown','orange','r','g','b','y','m','gray','black','c','pink','brown','orange','r','g','b','y','m','gray','black','c','pink']
for i in range(len(res)):
    nx.draw_networkx_nodes(G, pos, with_labels=True, node_color=color_list[i], nodelist=res[i])
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

结果：

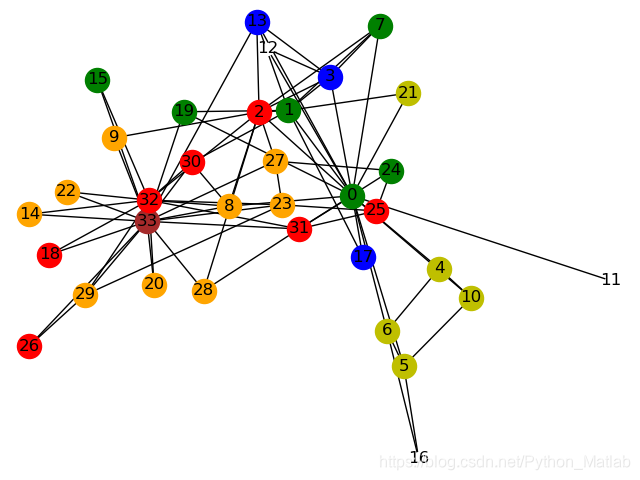
• 说在最后，因为是随机的，所以每次运行的结果可能是不一样的