- 1入门生成式语言模型(Generative Language Models)_用llama pro+moe架构
- 2Python标准库之Tkinter库详细教程_python tkinter
- 3人工智能会话代理在医疗保健中的有效性:系统综述_智能代理在医学的应用文献综述
- 425. 在QWidget窗口中嵌入QML界面_将qwidgets嵌入qml
- 5流量检测领域-数据集_网络流量异常检测数据集
- 6注册中心eureka的介绍及源码探索
- 7Ansible 1.5.8:unarchive 模块_ansible unarchive
- 8maven 常见问题处理_400 repository does not allow updating assets: mav
- 9领导之路_领导之路版权
- 10聊聊如何设计千万级吞吐量的.Net Core网络通信!
论文阅读--Q-Transformer: Scalable Offline Reinforcement Learning via Autoregressive Q-Functions
赞
踩
Abstract:
我们的方法通过使用Transformer通过离线时间差备份训练的为Q函数提供可扩展的表示。我们称我们的方法为Q-Transformer。通过离散每个动作维度并将每个动作维度的Q值表示为单独的token,我们可以将有效的高容量序列建模技术应用于Q学习。
Introduction
挑战:当前在机器人学习领域主要通过自监督的方式实现对算法的训练,这样训练出来的策略将受限于人类演示者的演示数据质量。首先,我们希望开发一种算法能够充分利用硬件的潜力、快速、流畅、可靠地执行任务。第二,我们希望机器人系统能够通过自主收集的经验变得更好,而不是完全依赖于高质量的演示。挑战:事实证明,使用RL算法训练诸如Transformer之类的高容量模型更难大规模有效地实例化。
在本文中,我们的目标是将来自不同真实世界数据集的大规模机器人学习与现代高容量基于Transformer的策略架构相结合。设计一种有效利用此类体系结构的方法要困难的多。只有当我们在大型和多样化的数据集上训练时,高容量模型才有意义——小型、狭窄的数据集根本不需要那么多容量,也不会从中受益。虽然之前的许多工作使用模拟来创建这样的数据集,但最具代表性的数据来自现实世界。因此,我们专注于强化学习方法,这些方法可以使用Transformer,并通过离线RL合并以前收集的大型数据集。离线RL旨在通过给定的数据集尽可能学习出最佳的策略。
当然,这些数据集可以通过额外的数据扩增但是训练与数据收集是分离开的,为大规模机器人应用提供了一个吸引力的工作流程。
由于Transformer对离散token序列进行建模,我们将Q函数估计问题转化为离散token序列建模问题,并为序列中的每个token设计合适的损失函数。对动作空间进行离散化会导致动作基数的指数膨胀,因此我们采用每维离散化方案,其中动作空间的每个维度都被视为RL的单独时间步长。离散化中不同的bin对应于不同的动作。每维离散化方案允许我们使用具有保守正则化项的简单离散动作的Q学习方法来处理分布偏移。
我们提出了一种特定的正则化项,该正则化项使数据集中未采取的每一个动作的值最小化,并表明我们的方法可以从狭窄的演示数据中和具有探索噪声的更广泛的数据中学习。我们使用了一种混合更新,它将蒙特卡洛和n-step returns与时间差backup相结合,并表明这样做可以提高我们基于Transformer的离线RL方法在大规模机器人学习问题上的性能。

从离线数据中学习策略需要求解分布漂移的问题,因为一般来说能够最大化Q值的动作可能位于数据分布之外。解决这种问题的一种方法就是通过低估分布外的动作的Q值,从而确保最大值动作是分布内的。
在我们的工作中,我们考虑稀疏奖励的任务,奖励只有0,1,并且仅在episode的最后一步才有奖励。我们的方法是不是仅仅针对这一种任务,但是这种奖励结构在机器人操纵任务中很常见,这些任务在每一集中要么成功,要么失败,也就是只有0,1。同样在Antmaze这样的迷宫游戏也是属于奖励稀疏问题。并且由于缺乏reward shaping,对于RL来说可能是特别具有挑战性的。
Q-Transformer
算法主体部分,分为三个部分介绍:
- 第一,介绍如何应用离散化和自回归使得TD-learning可以与Transformer框架结合;
- 第二,介绍一种保守Q函数正则化,能够从离线数据中学习;
- 第三,展示蒙特卡洛和n-step returns如何用于提升学习的效率。
Autoregressive Discrete Q-Learning 自回归离散Q学习
将Transformer与Q学习结合带来了两个挑战:
- 我们必须将输入token化以有效的应用注意力机制,这需要离散化动作空间
- 我们必须在离散化动作上实现Q值的最大化,同时避免维度的诅咒curse
在标准化Q学习框架内解决这些问题需要新的建模决策。我们的自回归Q学习更新背后的直觉是将每个动作的维度本质上视为一个单独的时间步长。这样,我们可以离散单个维度,而不是整个动作空间,避免维度的诅咒。
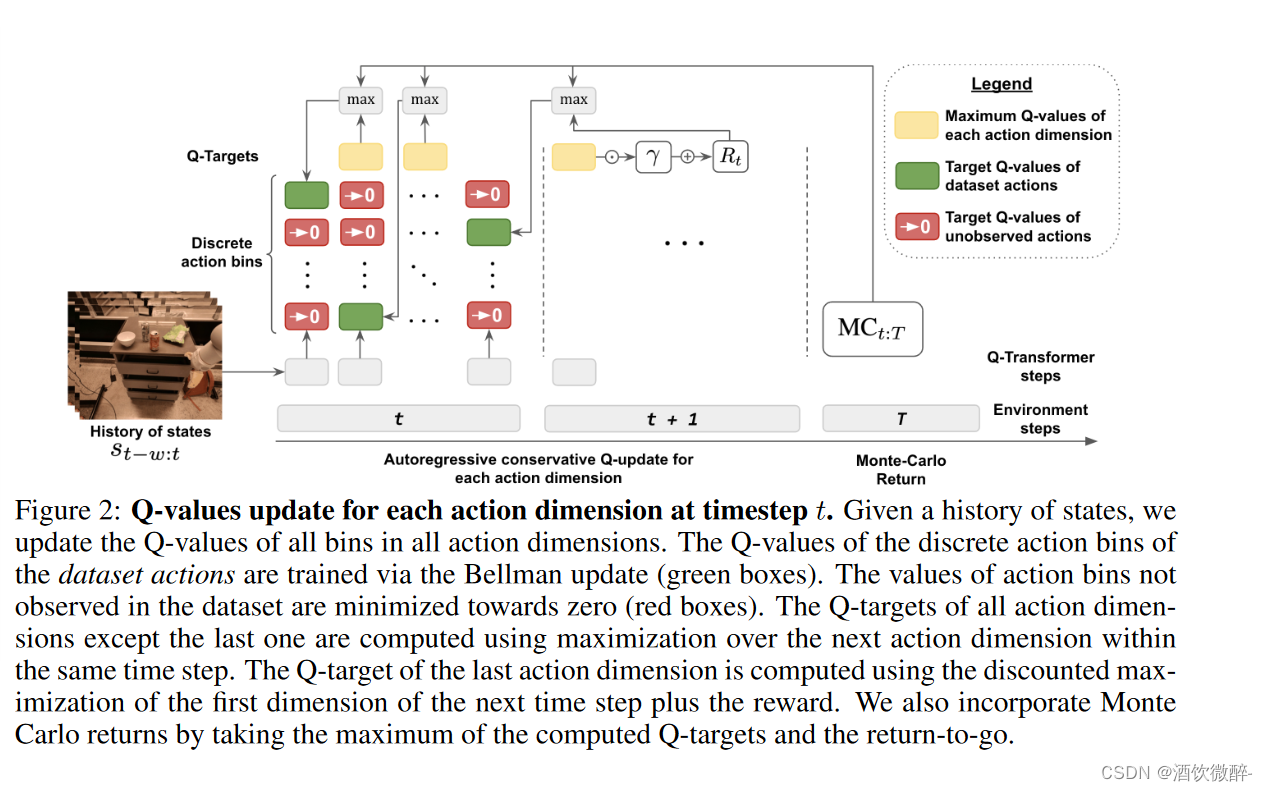
在呈现最终目标时省略了动作维度索引
当数据集包含一些好的轨迹和一些次优轨迹时,利用蒙特卡洛回归估计来加速Q学习可以显著提高性能,因为沿着更好轨迹的蒙特卡洛估计会导致更快的值传播。
Experiment
实验部分主要通过实验验证回答了以下四个问题:
(1) Can Q-Transformer learn from a combination of demonstrations and sub-optimal data?
(2) How does Q-Transformer compare to other methods?
(3) How important are the specific design choices in Q-Transformer?
(4) Can Q-Transformer be applied to large-scale real world robotic manipulation problems?
Limitations and Discussion
首先,我们专注于稀疏的二进制奖励任务,对应于每次试验的成功或失败。虽然这种设置对于广泛的偶发机器人操纵问题是合理的,但它并不具有普遍性,我们希望 Q-Transformer 在未来也能扩展到更广泛的环境中。
其次,我们采用的按维度动作离散化方案在更高维度(如控制仿人机器人)时可能会变得更加繁琐,因为我们模型的序列长度和推理时间会随着动作维度的增加而增加。
统一的动作离散化也会给需要大范围动作粒度(如粗动作和细动作)的操纵任务带来问题。在这种情况下,可以使用基于动作分布的自适应离散化来表示这两种类型的动作。
参考且转:


