【哈夫曼树】创建哈夫曼树_哈夫曼树的创建

基础概念：

什么是路径？

在一棵树中，从一个结点到另外一个结点所经过得所有的结点，我们成为两个结点之间得路径。

从A到叶子结点E的路径就是：A->B->D->E;

什么是路径长度？

在一棵树中，从一个几点到另外一个结点所经过的边的数量，就是路径长度。

从根结点A到叶子结点E，共经过了3条边，因此路径长度是3。

什么是【结点】的带权路径长度？

树的每一个结点，都可以拥有自己的“权重”（weight），权重在不同的算法中起到不同的作用。
结点的带权路径长度 = 树的根节点到该结点的路径长度 * 该结点权重。

假设结点E的权重是2，从根结点到结点E的路径长度是3，因此E结点的带权路径长度为：2*3 = 6

什么是【树】的带权路径长度？

在一棵树中，所有的叶子结点的带权路径长度之和，被称为树的带权路径长度，简称WPL

• 下面讲一下：什么是哈夫曼树？

我们知道了树的带权路径的计算方式，哈夫曼就是在树的叶子结点和权重确定的情况下，带权路径最小的二叉树即为 最优二叉树（也就是哈夫曼树）

给定权重 1 ，2 ，3 ，4

明显右边小于左边。 因此右边就是哈夫曼树。

但是哈夫曼树不止一种。
如下：

如何构建一棵哈夫曼树？

共有6个叶子结点，权重分别是：1，4，7，11，22，32

1.构建森林：

把每一个结点都当做一棵独立的树。因此便形成一片森林

• 左侧为辅助队列，右侧为叶子结点的森林。根据两个结点生成一个新的父结点，父节点的权值是两个结点的权值之和。
  
• 选择当前队列中最小的两个结点，生成新的父节点。移除队列中的两个最小结点。并将信的父节点加入到队列。
  
  

当队列中仅有一个结点，说明整个森林已经合并成一棵树，这棵树就是哈夫曼树。

• 权值越小，离根越远。
  
  

如果出现相加和与待选择权重队列中的重复，则可以选择新加入的或者原队列中的均可。
最终：

设计哈夫曼树

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<queue>
using namespace std;

const int n = 8;//leaf 
const int m = n * 2;//node
typedef unsigned int WeightType;
typedef unsigned int NodeType;
typedef struct {
	WeightType weight;
	NodeType parent, leftchild, rightchild;
}HTNode;

typedef HTNode HuffManTree[m];//静态存储 数组类型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

优先级队列：（priority_queue）

基本概念： 不满足先进先出的条件，更像是数据类型中的堆，优先级队列每次出队的元素不是队首元素，而是优先级最高的元素，这个优先级可以通过元素的大小进行定义。
比如定义元素越大优先级越高，那么每次出队，都是将当前队列中最大的那个元素出队。
现在看优先级队列是不是就是“堆”了，如果最大的元素优先级最高，那么每次出队的就是当前队列中最大的元素，那么队列实际就相当于一个大顶堆，每次将堆根节点元素弹出，重新维护大顶堆，就可以实现一个优先级队列。

priority_queue<typename, container, functional>
1

typename是数据的类型；
container 是容器类型，可以是vector,queue等用数组实现的容器，不能是list，默认可以用vector；
functional是比较的方式，默认是大顶堆（就是元素值越大，优先级越高）；

• less重载小于“<”运算符，构造大顶堆；
• greater重载大于“>”运算符，构造小顶堆
• 举个栗子：
  构造一个大顶堆，堆中小于当前节点的元素需要下沉，因此使用less

priority_queue<int, vector<int>, less<int>> p;
1

构造一个小顶堆，堆中大于当前节点的元素需要下沉，因此使用greater

priority_queue<string, vector<string>, greater<string>> p;
1

打印哈夫曼树

void Print_HuffManTree(HuffManTree hft)
{
	for (int i = 1; i < m; ++i)
	{
		printf("index :%3d weight: %3d parent :%3d left:%3d right: %3d\n",
			i, hft[i].weight,hft[i].parent,hft[i].leftchild,hft[i].rightchild);
	}
}
1
2
3
4
5
6
7
8

初始化哈夫曼树

void Init_HuffManTree(HuffManTree hft, WeightType weight[])
{
	memset(hft, 0, sizeof(HuffManTree));
	for (int i = 0; i < n; ++i)
	{
		hft[i+1].weight = weight[i];  //初始化权重
	}
	//printf("HuffmanTree = %d\n", sizeof(HuffmanTree));
	//printf("hft:    size %d\n", sizeof(hft));
	//printf("w:    size%d \n", sizeof(weight));
}
1
2
3
4
5
6
7
8
9
10
11

创建哈夫曼树

struct IndexWeight
{
	int index; //下标
	WeightType weight;//权值参与比较
	operator WeightType() const { return weight; }
	  //把weight强转为WeightType类型
 };



void CreateHuffManTree(HuffManTree hft)
{
	priority_queue<IndexWeight, vector<IndexWeight>, std::greater<IndexWeight>> qu;
	for (int i = 1; i <= n; ++i)
	{
		qu.push(IndexWeight{ i,hft[i].weight });
	}
	int k = n + 1;
	while (!qu.empty())
	{
		if (qu.empty()) break;  //将最小的两个值出队列
		IndexWeight left = qu.top(); qu.pop();
		if (qu.empty()) break;
		IndexWeight right = qu.top(); qu.pop();
		hft[k].weight = left.weight + right.weight;
		hft[k].leftchild = left.index;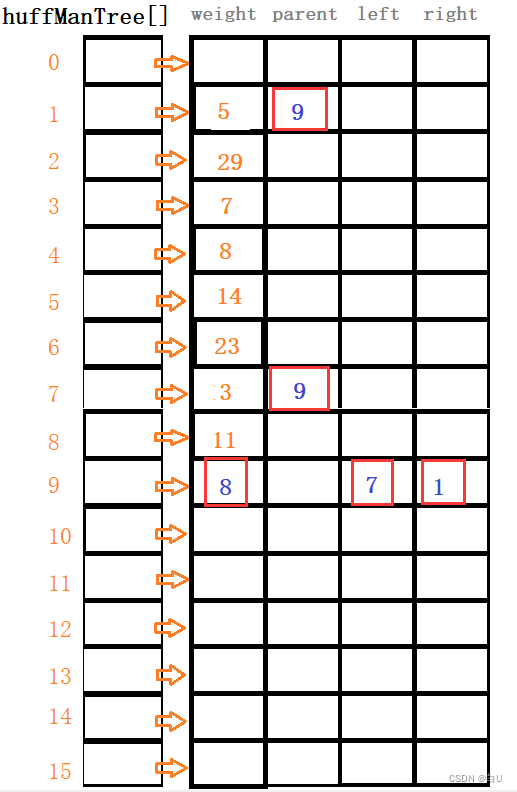![请添加图片描述](https://img-blog.csdnimg.cn/9e05122ea843401d88ad5b77ec6dece7.png)

		hft[k].rightchild = right.index;
		hft[left.index].parent = k;
		hft[right.index].parent = k;
		qu.push(IndexWeight{ k,hft[k].weight });
		k++;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34