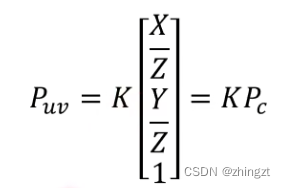三维重建知识准备_mvs

1 sfm与mvs基本流程

            MVS三维重建概述与OpenMVS开源框架配置

        openMVS——基础开源mvs方法中做的还不错的（自己尝试过在ubuntu和windows系统上进行配置，均未成功）

2 三维重建的基础（几何等）

        这些概念主要来源于《视觉SLAM十四讲》，视觉SLAM和MVS是很像的概念。所以可以借以参考。可以对一些视差、基线、cost volume的概念有基本的认识，方便后续持续推进。

        参考如下视频与链接：

         立体视觉的几何基础总结

        视觉SLAM十四讲_1 2初识SLAM_哔哩哔哩_bilibili

        【SLAM】高翔-视觉SLAM十四讲 配套视频_哔哩哔哩_bilibili

        2.1 第一第二讲 初识slam

        两大问题：

        

        相机的分类

              

        what is 基线（baseline）。应该就是视差中提到的基线。两个视角光心之间的距离？         

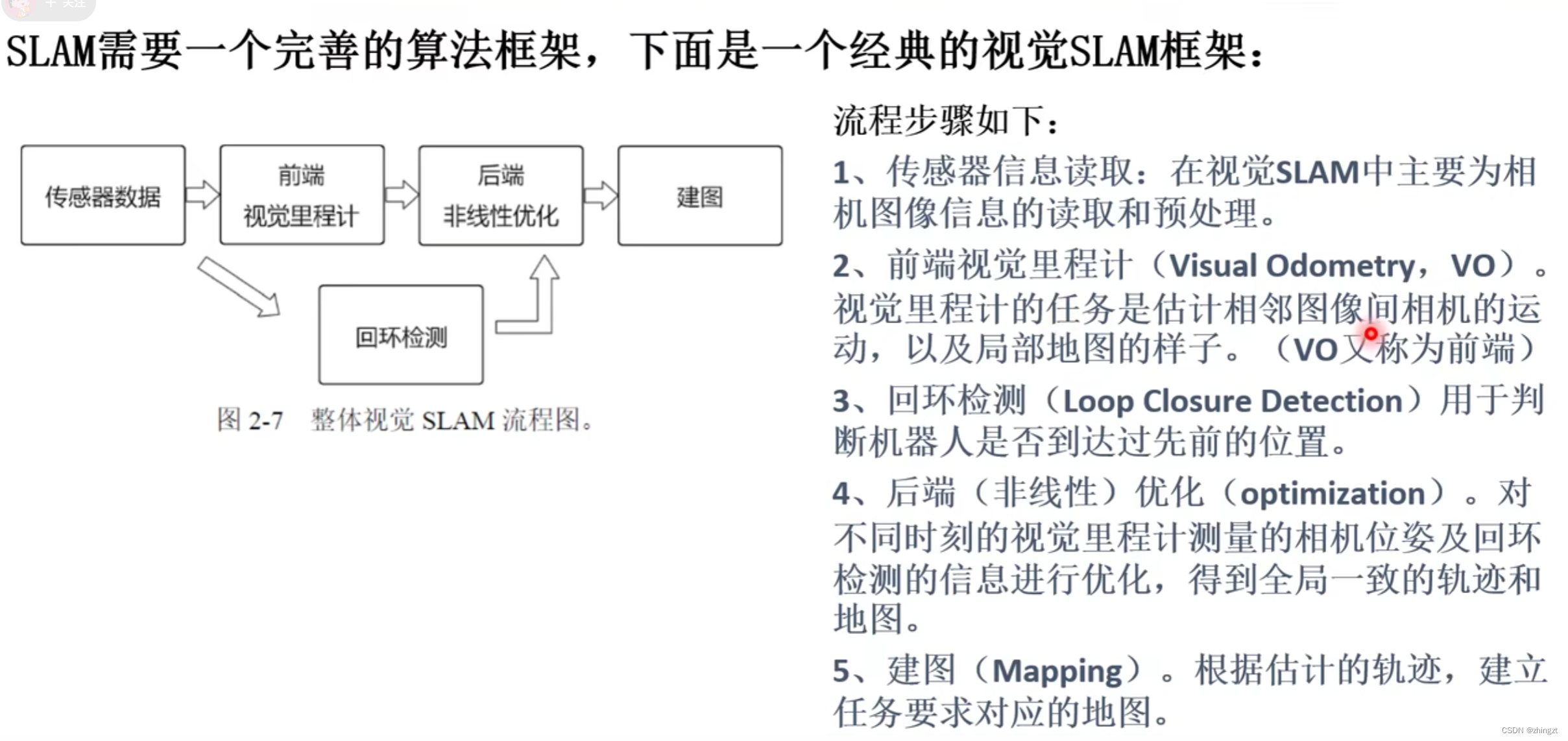
        经典视觉slam框架        

        2.2 第三讲 三维空间的刚体运动

        2.2.1 点、向量和坐标系、旋转矩阵

         对相机的描述可以用    位置和姿态  进行描述。位置就是(x,y,z)，姿态就是相机的朝向。怎么用数学语言进行描述呢？

        对于坐标而言，只有定义坐标系，才可能在这个坐标系下谈论它的坐标。

        向量可以用坐标系下的坐标进行表述。

        向量的运算就可以由坐标运算进行表达，主要对外积做一个补充说明

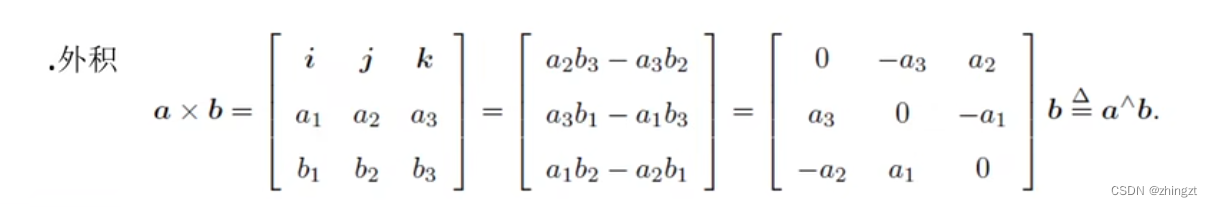
        不同的坐标系下是怎么变化的？

                分为   1）三个轴的旋转  2）原点的平移（就是一个向量）。

        怎么去描述这个旋转。

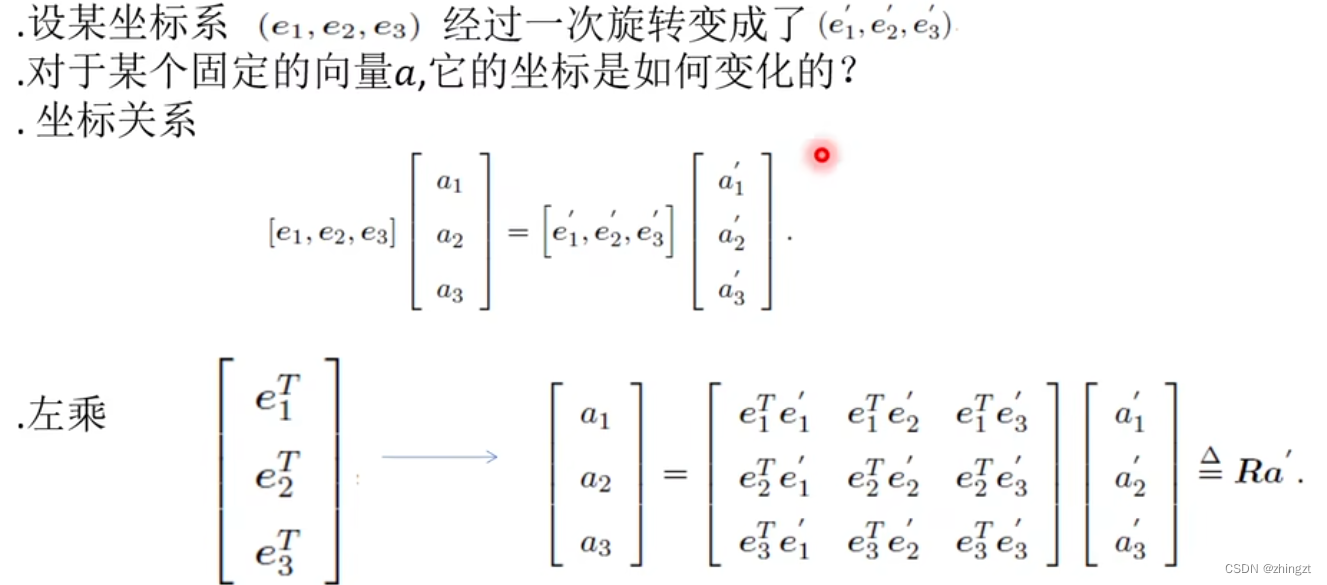
         关键点：正交矩阵（矩阵的逆和矩阵的转置相同——说明不同坐标系下的互相转化只需要将旋转矩阵R转置即可了）—— 行列式为1。

 

        2.2.2 齐次坐标和变换矩阵

        （1）why 提出齐次坐标

        为了使向量在多个坐标系下的连续变换的格式简单。

        

        （2）怎么提出齐次坐标

        齐次坐标就是最后一位为1.

        因为发现，我们同时拥有旋转矩阵和平移向量，那么如果能够把平移向量写到矩阵里面，那么就可以直接乘以这个矩阵，而不用额外再加向量。

        

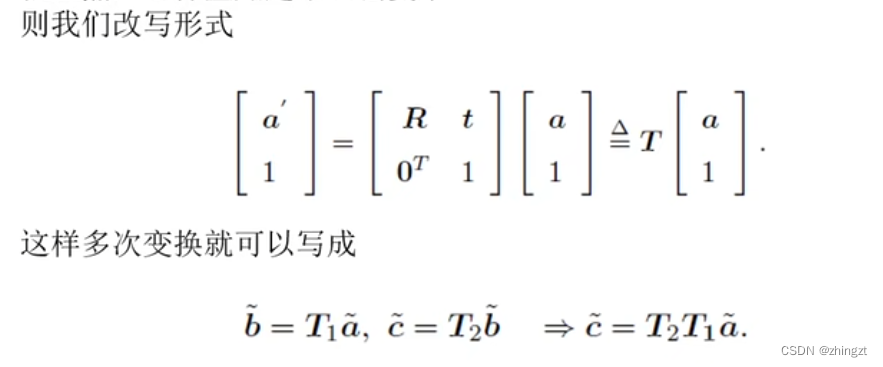
        这个时候我们就用四个数来表达三维向量（也就是在最后一维加个1），称之为齐次坐标

         旋转和平移就放在了同一个矩阵中，称为变换矩阵T。

        

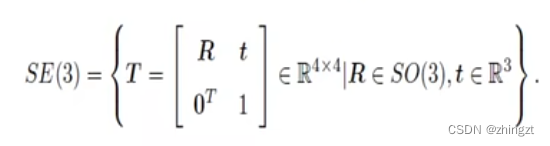
        这样的SE(3)称为特殊欧式群。

        

        注意这里的平移向量就变成了-RTt

        实际上旋转矩阵只有三个自由度，平移向量也是三个自由度，所以总共只有六个自由度。希望找到一个更紧凑的表达，不要隐含太多约束。

         2.2.3 旋转向量

         关键点：旋转向量w的方向为旋转轴，长度为转过的角度。（感觉上没有一个很直观的几何意义在）

        

        旋转向量和旋转矩阵之间的转换

       

        （换句话说，转轴是矩阵R特征值1对应的特征向量）（旋转轴上的向量在旋转后不发生改变）

        （tr表示矩阵的迹，就是对角线元素之和）

        2.2.4 欧拉角（yaw、pitch、roll)

        事实上我们会发现，坐标系间的转动并没有很直观，所以希望找到一个更让人能够理解的方式去表达。

        其中就可以借助所谓的欧拉角。

     

        

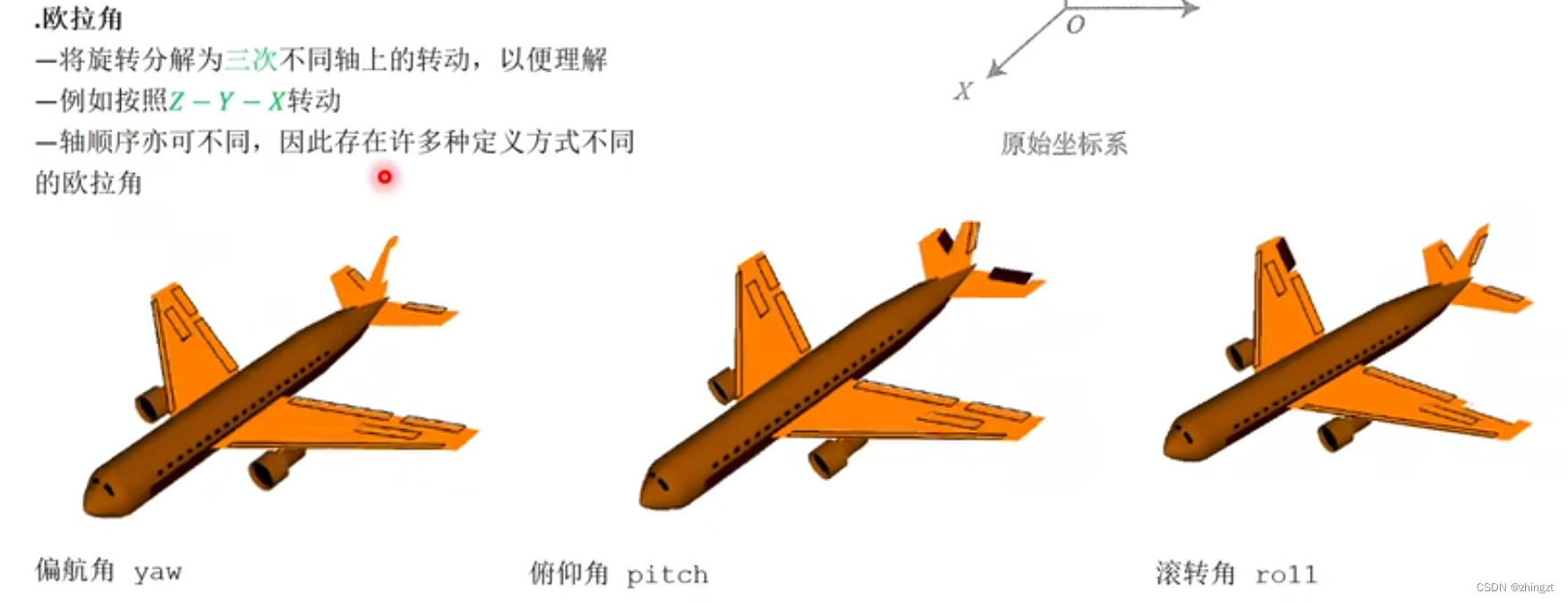
        注意，此时x轴、y轴都是随时改变的。

        欧拉角遇到的万向锁问题（自由度丢失的问题）。此时会导致矩阵奇异，发生问题。

        

        欧拉角和旋转向量是紧凑的，但具有奇异性。事实上，找不到不带奇异性的三维向量描述方式。

        2.2.5 四元数

        紧凑且不奇异的去描述三维空间中的旋转。单位四元数本身还有一个约束（就是模长为1）

         四元数的性质：

        1）单位四元数的逆就是共轭（虚部取为相反数）

        2）

        

         2.2.6 四元数和旋转向量、旋转矩阵的关系

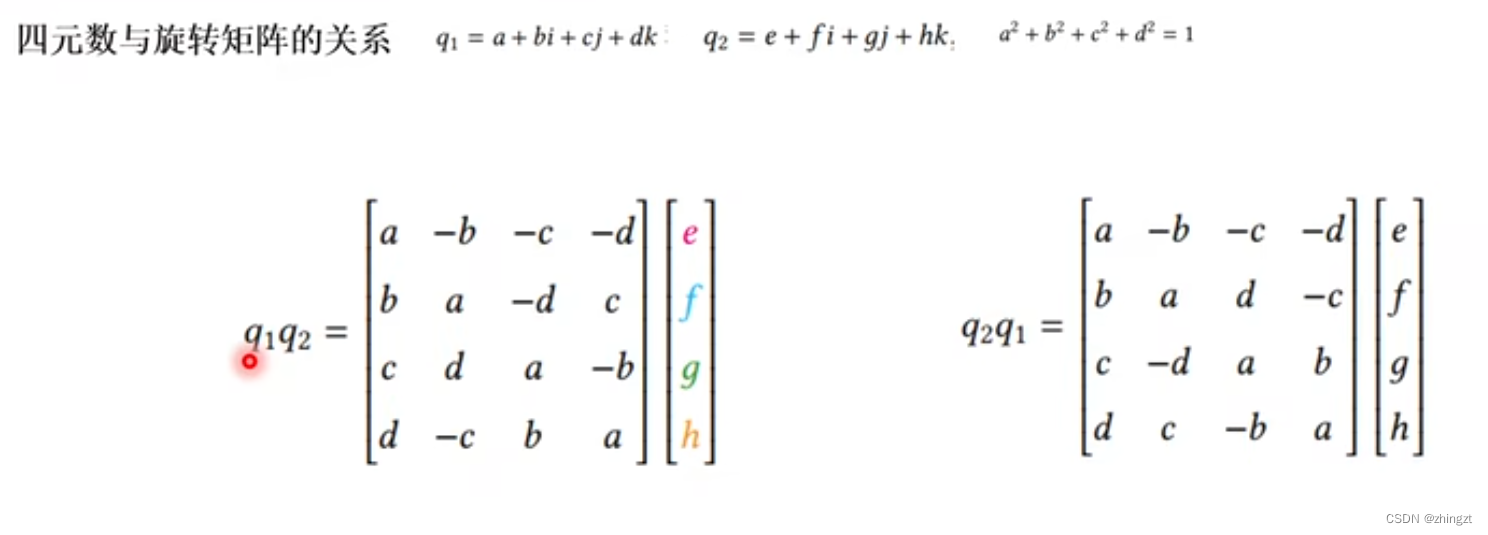
        2.3 第四讲 李群与李代数（SLAM优化中用的比较多,MVS不涉及，暂且跳过）

        SLAM的过程就是估计机器人的位姿，也就是不断估计变换矩阵。

        为了进一步的估计和优化，需要对变换矩阵进行插值、求导、迭代等操作。

        1）我们希望让这个损失函数J对T求导，但是怎么求导？

        2）T对乘法封闭，但是对加法不封闭。封闭是什么意思？

        所以我们要引出李代数和李群

 

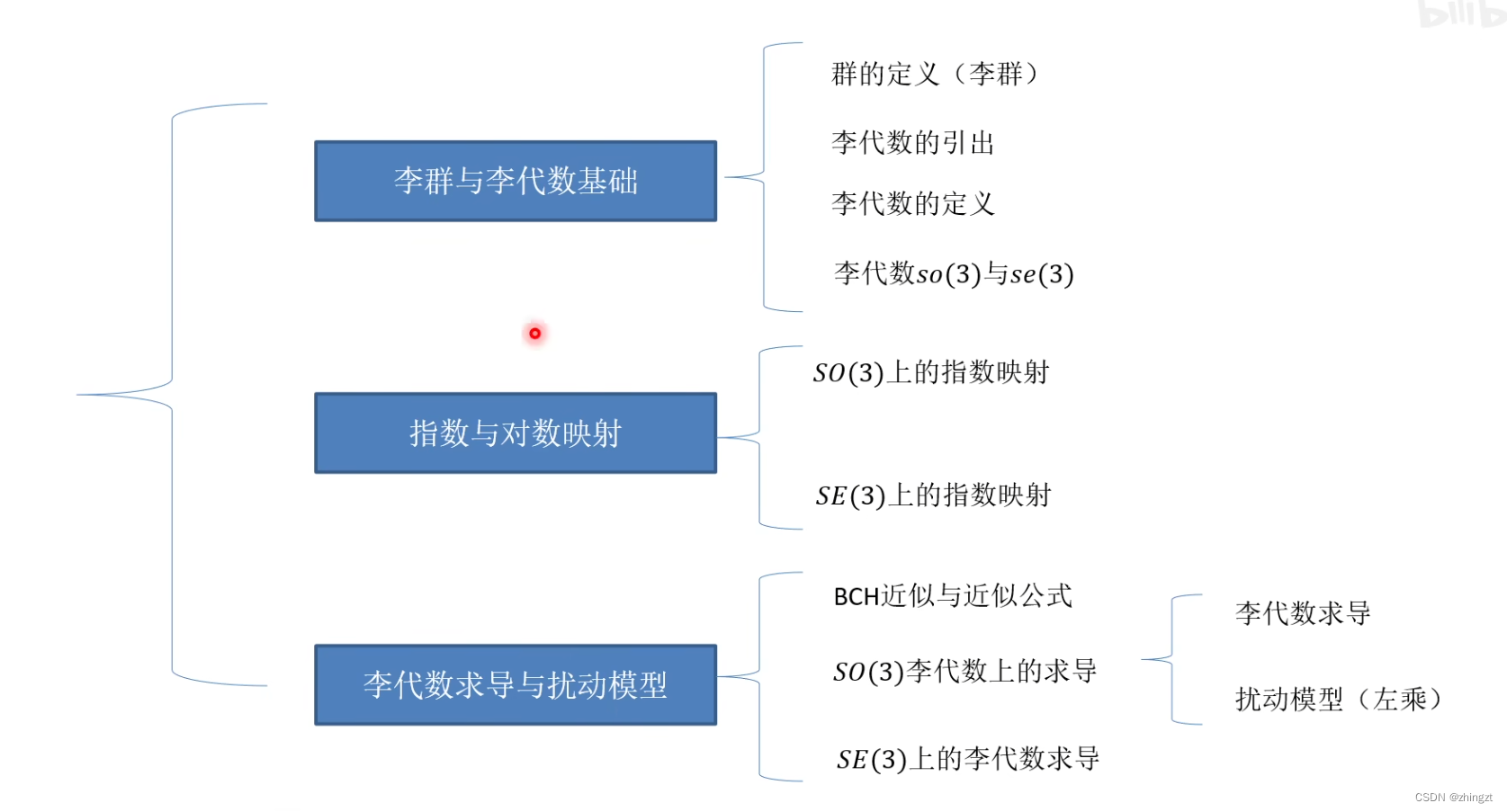
         2.3.1 李群和李代数基础

        2.4 第五讲 相机与图像

        相机模型是将三维世界中的坐标点（单位为m）映射到二维图像平面（单位为像素）的过程。丢弃了距离维度的信息（因为直接投影）。

        但在投影过程中，由于透镜的存在，光线投影到成像平面会产生畸变。描述整个投影过程：针孔和畸变模型（构成相机的内参数）。

        2.4.1 单相机模型

        （1）相机坐标系和成像平面的关系

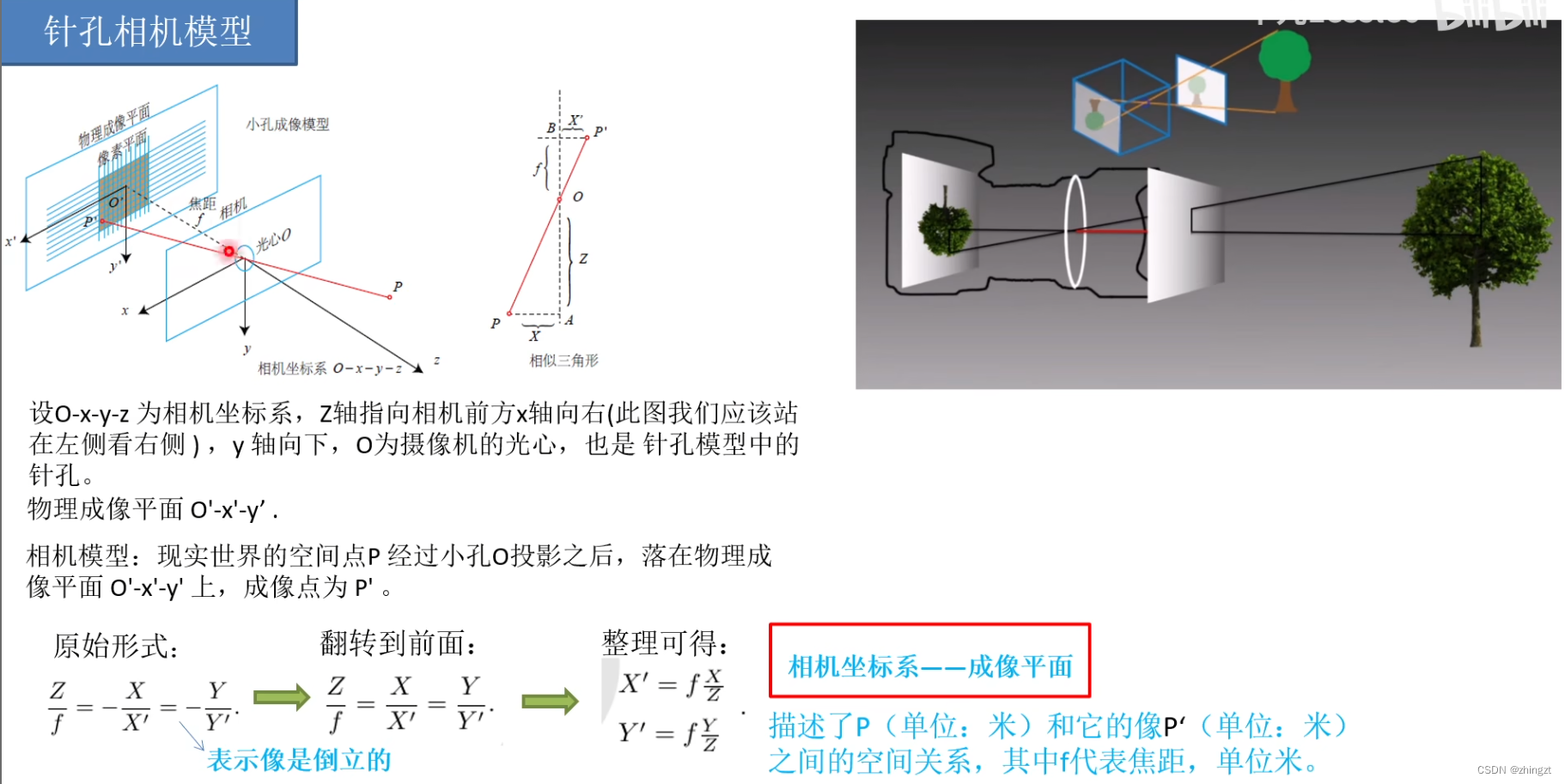
         右图向我们展现了相机简单的外部构造和简单内部结构）

        相机光心平面、成像平面  可构成一相似三角形。

        经过小孔、会使得图像上下颠倒、左右颠倒。（这也是为什么原始相似三角形等式中还存在负号的原因）。

        相机内部往往会做一个内处理。把倒立的像正过来。

        这个时候的相似三角形就描述了原始世界点P、像P‘和相机内部本身特征f、Z之间的关系。

        （2) 成像平面到像素坐标的关系

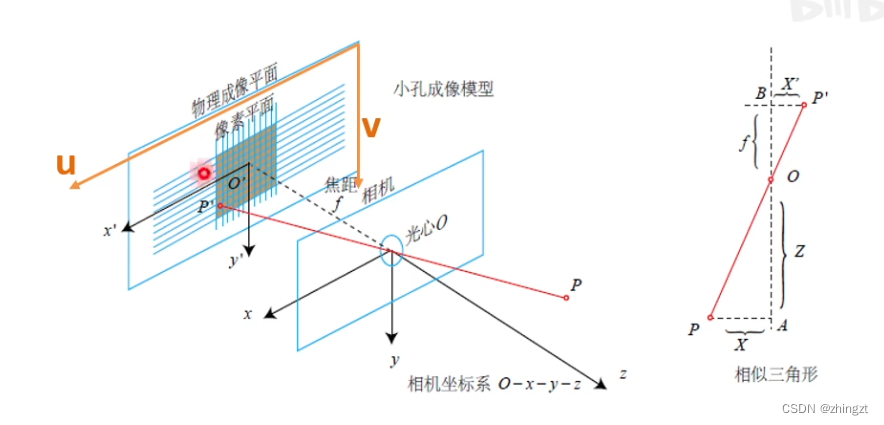
         像素坐标也就是平面图像上的每一个像素点的坐标（也就是我们能够对图像处理得到的一个坐标）。是一个二维坐标系。

        像素坐标系通常的定义关系：原点位于图像的左上角，u，v分别表示width和height方向。

        也就是说像素坐标系和成像平面之间，相差了一个缩放和一个原点的平移。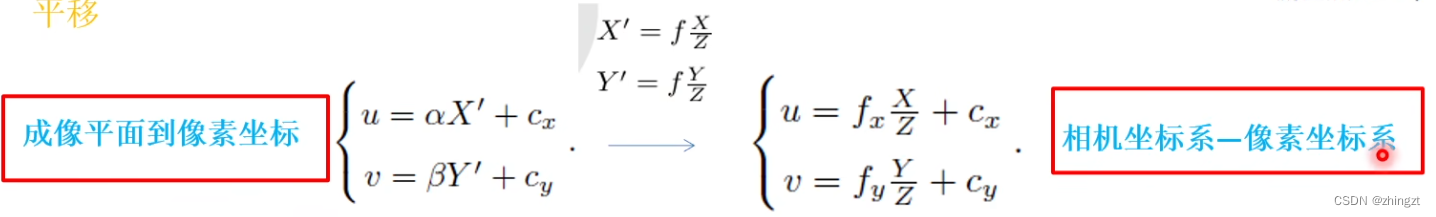        

         根据上述（1）（2）的公式，也就可以得到相机坐标系到像素坐标系的关系。

         *** 有个问题 fx，fy是指什么？

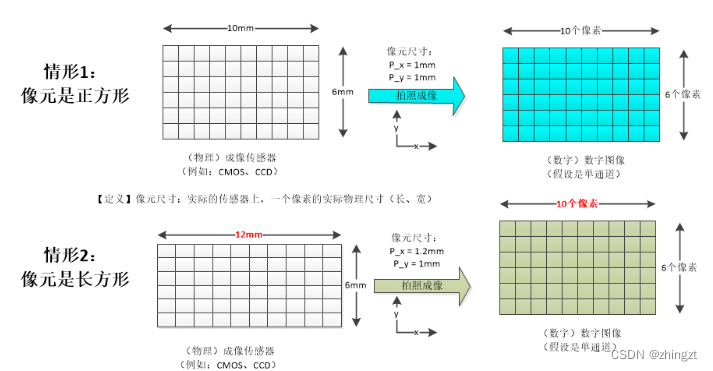
        一个相机的焦距f是确定的，但是在内参矩阵中需要用像素值去描述f，但是对于传感器而言，像元可能为非正方形。这就导致在传感器中，x方向和y方向的像素代表的实际长度不同。所以会出现不同的fx和fy。

        为了更好的写成矩阵形式，同样的再次提出齐次坐标（这样能让二维坐标和三维坐标保持同样的length，从而能够用矩阵形式相等）        

         内参矩阵的单位为像素。

        其实可以把上述的关系绘制在如下的图中：

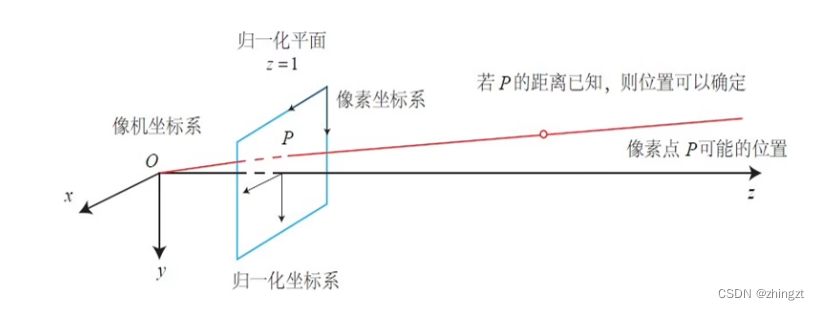
         所以实际上在这条延长线上的所有点的投影其实都是p，所以丢失了深度信息。

        z = 1的时候为归一化平面。

         像素坐标和相机坐标是差了内参矩阵的。

        （3）世界坐标系到像素坐标系的关系

        世界坐标系和相机坐标系之间还差一个变换，这个变换就称之为外参。

        

         这个T也就是上面第三讲中提到的刚体运动变换矩阵。        

       

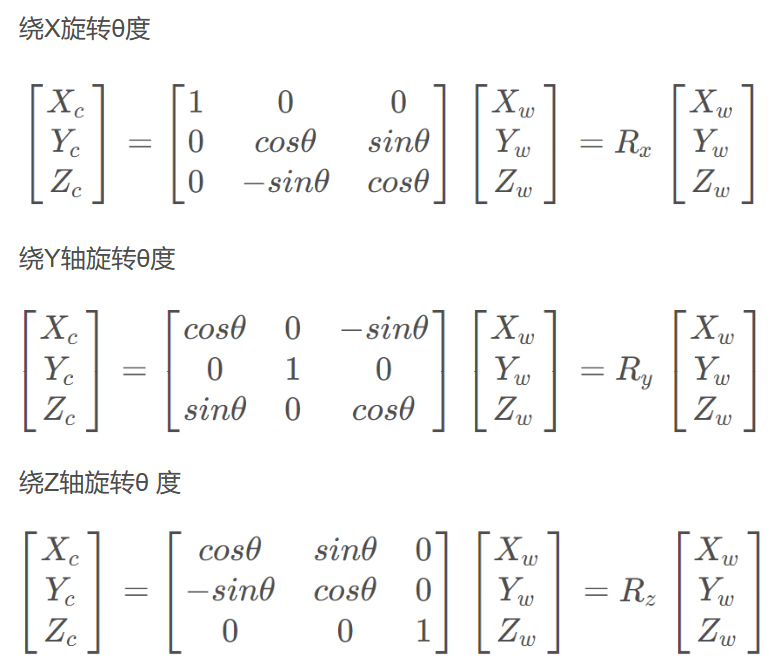
         2.4.2 畸变模型

        注意区分原点和光心，原点是指图像左上角，光心是指透镜中心同轴的那个点（基本就认为是图像的正中心）

        （1）径向畸变

        由于透镜的存在，光线的传播并非是一条直线。

        可以认为是在x、y方向上有个平移？

        因此，实际拍摄中，摄像机的透镜往往使得真实环境中的一条直线在图片中变成了曲线，越靠近图像边缘，这种现象越明显。

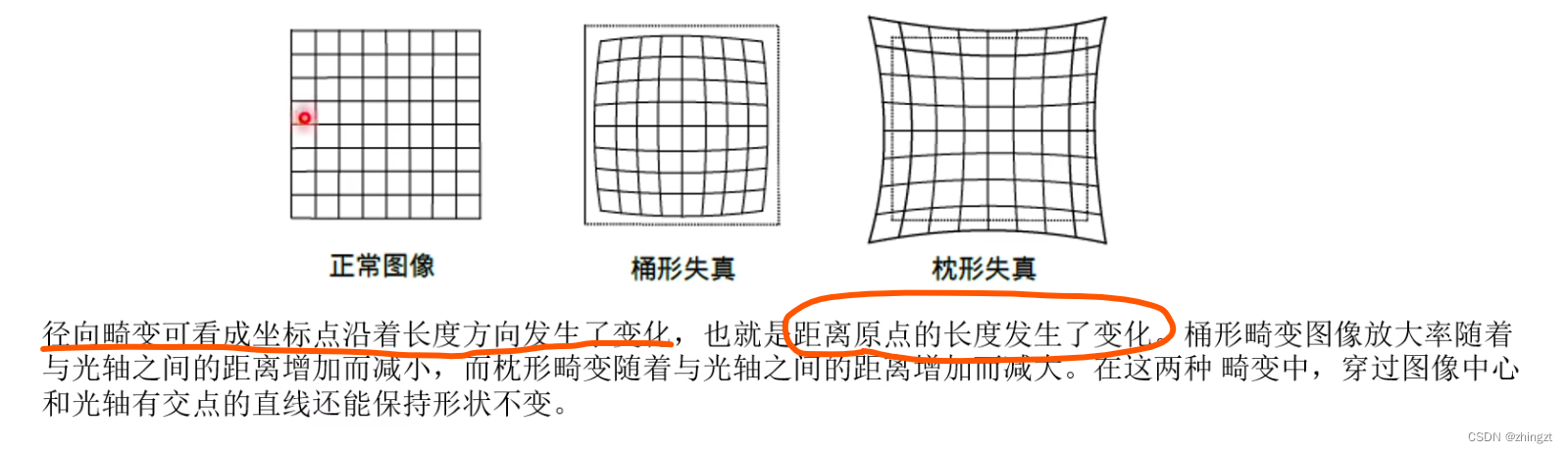
          （2）切向畸变

        相机组装过程中，不能使得透镜和成像平面严格平行会引起切向畸变。

         可以认为是水平夹角发生了变化。（在极坐标平面中）

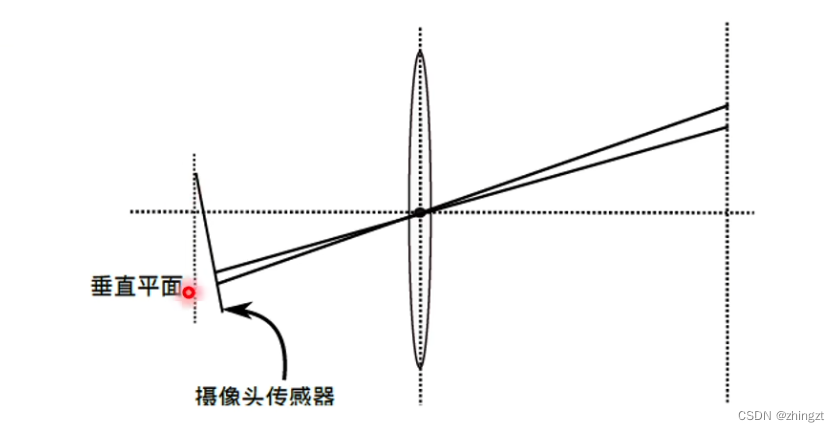
        （3) 数学模型描述        

         实际中，也可以把6阶项的系数省去，只保留其余项。（事实上也不是保留的越多精度越高，why？）

        这里的x(distorted)是指畸变后的坐标，x是指去畸变后的坐标。

        （4）具体代码

         对代码做简单理解，首先uv的坐标系是像素坐标（图像左上角为原点，向右向下）。xy的坐标系是归一化坐标（原点在光心，并且除以焦距）。distorted是指畸变后的坐标。

        也就是先遍历每个像素，根据每个像素去找到畸变后的像素坐标，再把那个畸变坐标位置上的值（亮度值、灰度值等等）赋给遍历时的像素。这样就得到了去畸变后的图像。

         2.4.2 双目相机模型

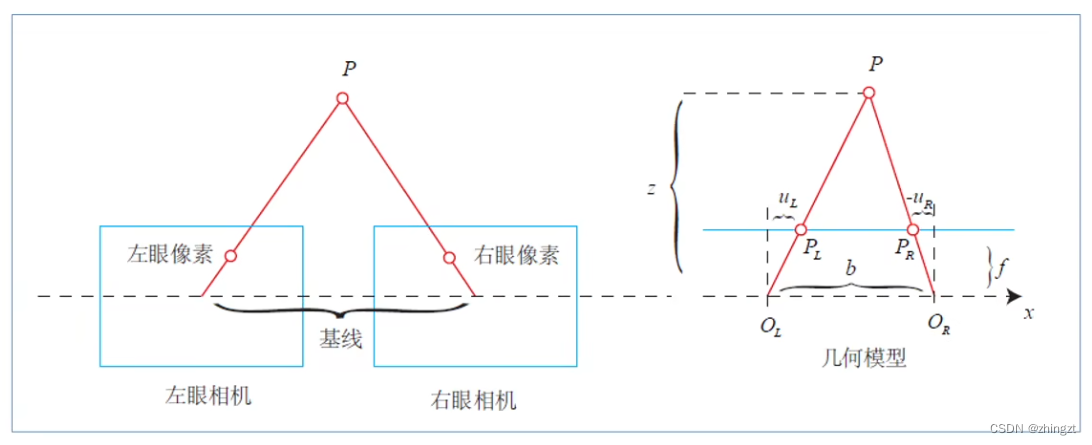
         左右相机（均视为单目相机）光心的距离就是基线

        根据几何模型（相似模型）可以推导得出：

        

         其中 d 是 P 在两个单目相机下像素坐标的距离（横坐标之差）也就是视差

        视差与距离成反比。

        2.4.3 RGB-D相机模型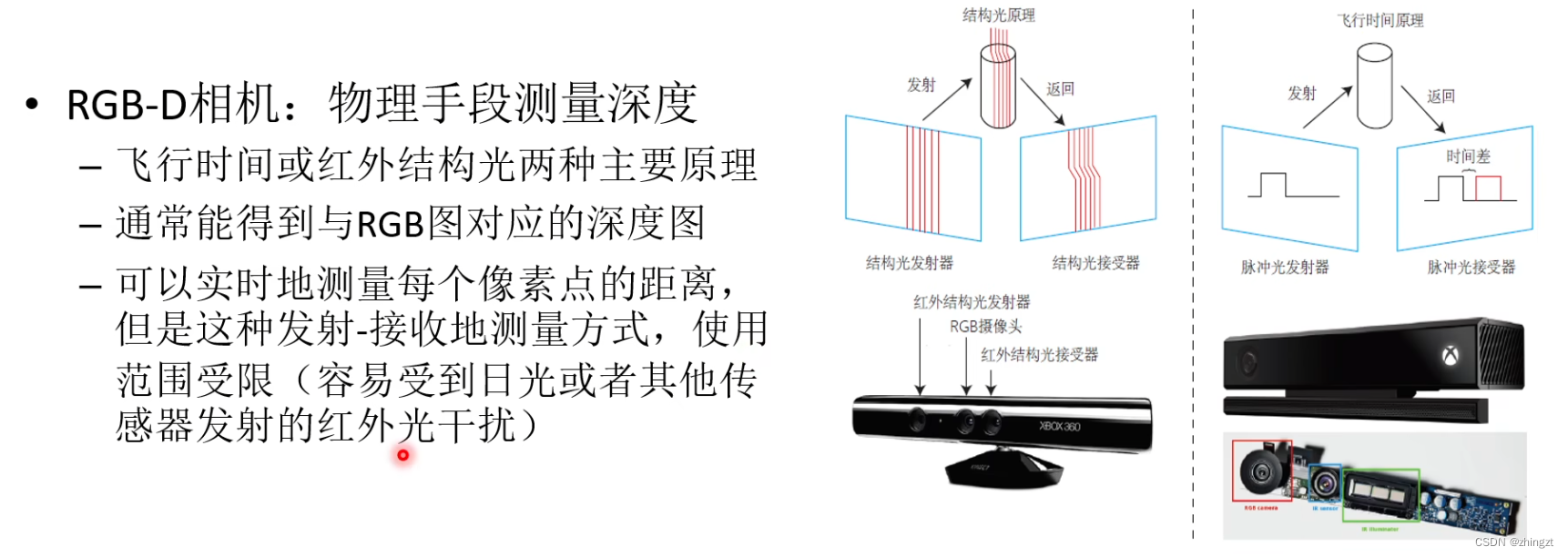        

         2.4.4 图像

         注意图像矩阵是行数、列数！（换句话说也就是访问第几行、第几列的元素，此时分别对应图像的高度y和图像的宽度x。)

        opencv里面图像颜色顺序为B\G\R。

        2.5 第六讲 非线性优化

        2.5.0 出发点与做了件什么事

        2.6 第七讲 特征提取与匹配

        2.6.1 特征点提取

        （1）特征点性质        

         对其中的几个性质做个简单解答：

        高效率：控制特征点数量不能过多

        （2）特征点的信息（包含的内容）

        

        （3）ORB特征

        3.1）关键点(oriented FAST) 一种改进的FAST角点

        怎么找FAST角点？

         FAST角点改进

        a) 非极大值抑制

        why we need nms？

        因为可能在某些区域会出现FAST角点扎堆的情况，所以某个区域里会只保留响应是极大值的角点，避免这种扎堆和集中的情况。

        b) 尺度问题

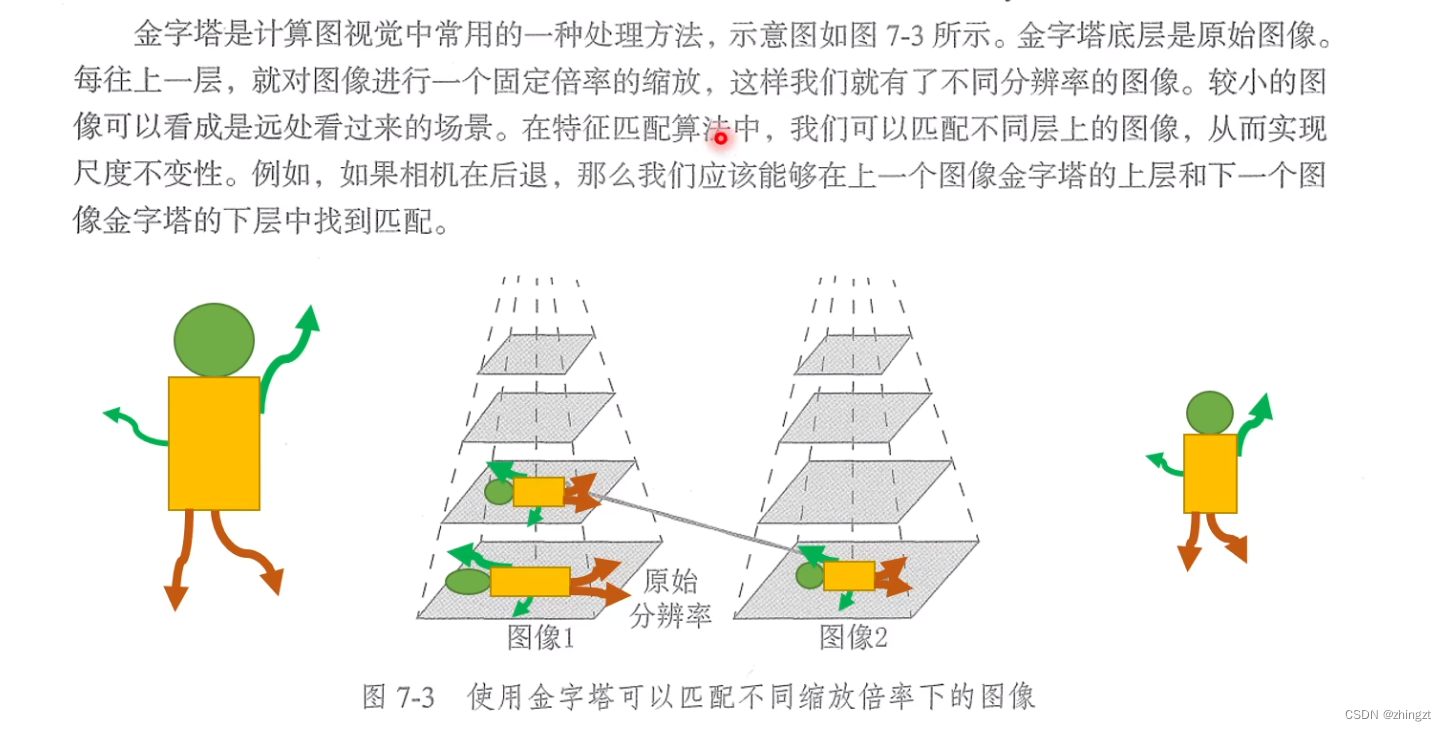
          c）方向问题

        

        3.2）描述子

         

         3.3）基本过程

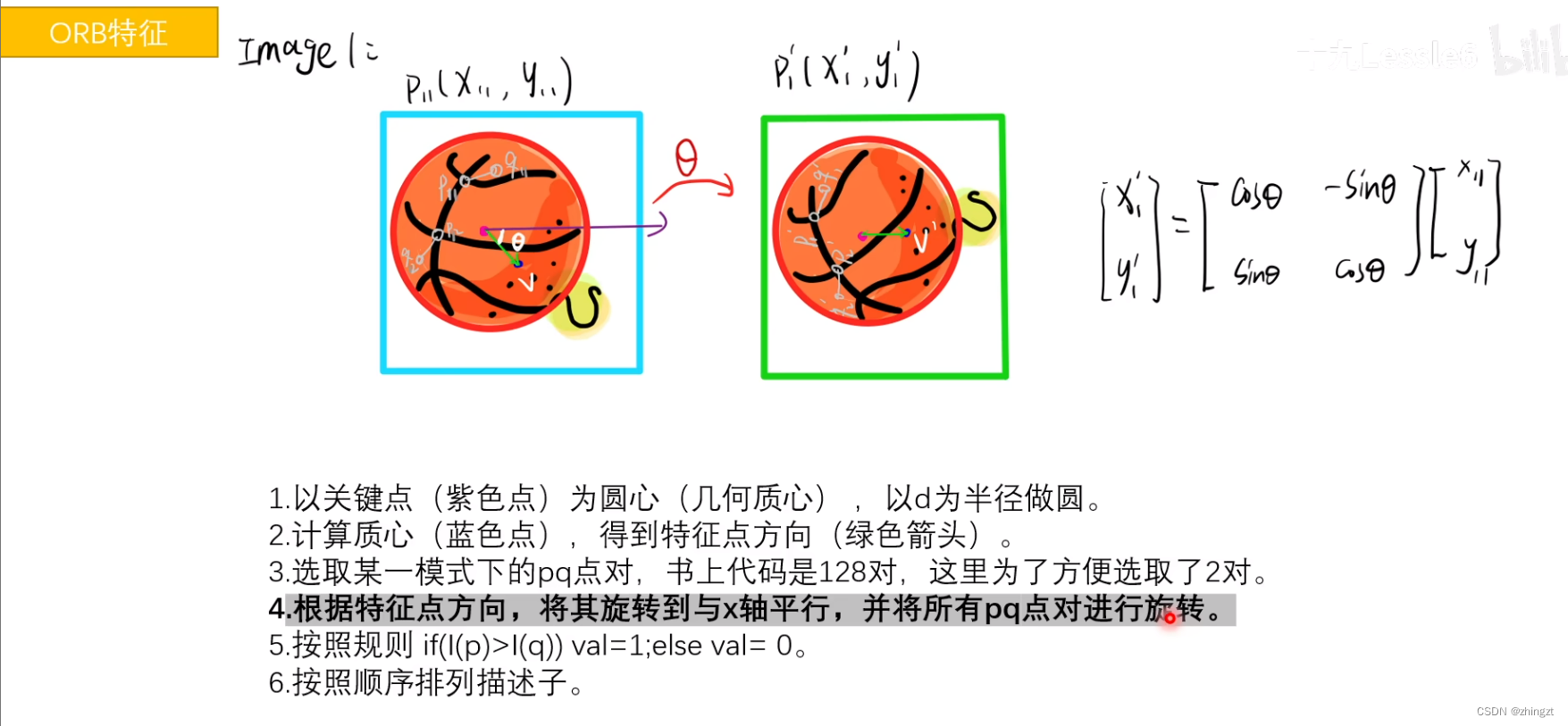
         正因为有了这样的一个方向向量，所以可以达成旋转不变性（因为最后都能调整回来）

        2.6.2 特征点匹配

        

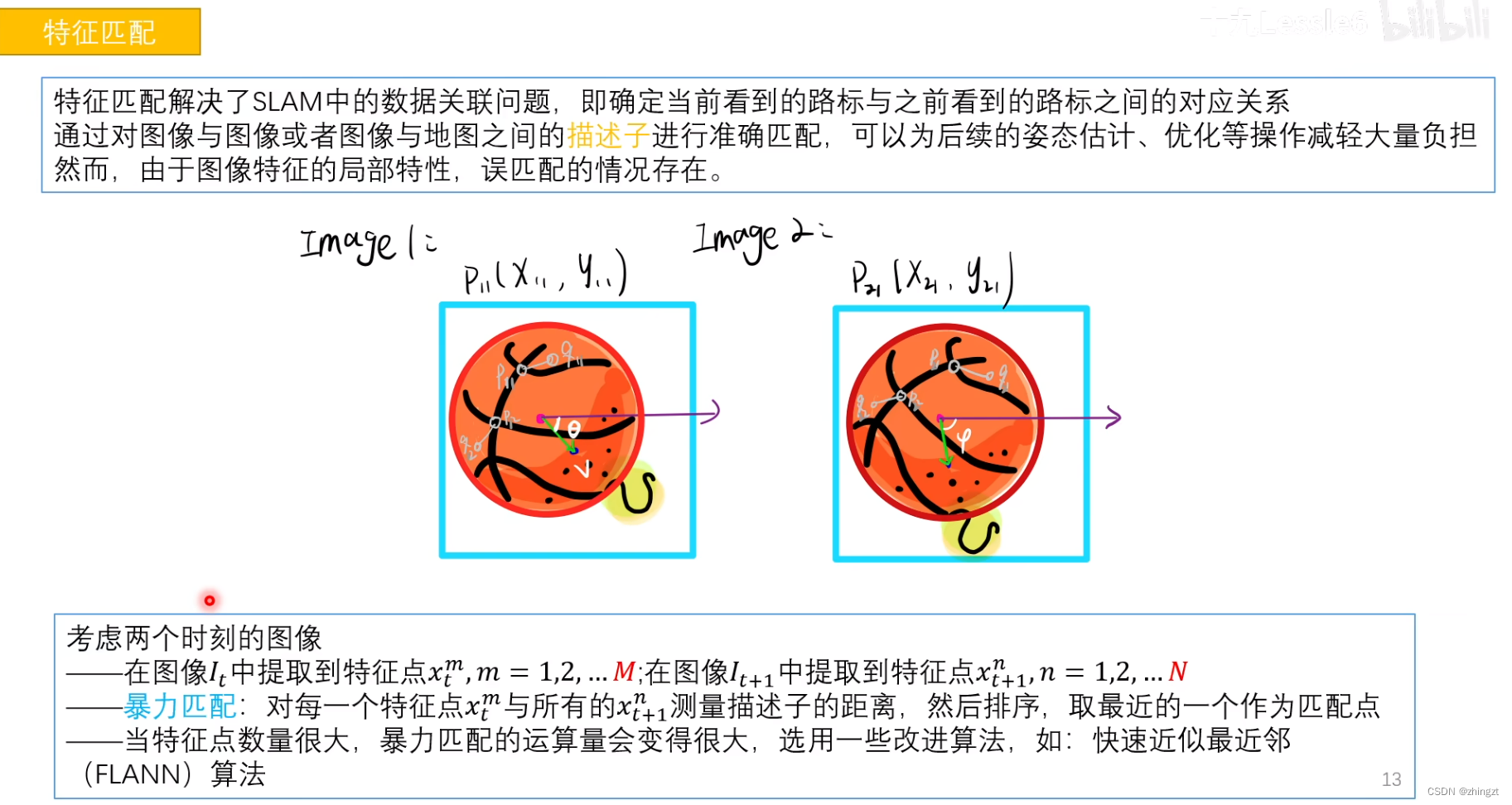
        2.7 第八讲 计算相机运动

        包括（1）两个单目图像得到2d-2d的关系 对极几何   （2) 得到3d和2维图像投影的关系 3d-2d关系（PNP)  (3) 当相机能够自主得到距离信息（比如RGB-D），就可以得到3d-3d的关系（ICP）

        2.7.1 2D-2D  对极几何问题

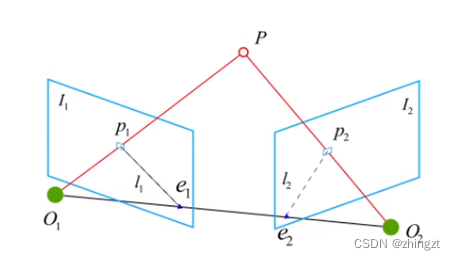
        注意这里的O1O2分别为两个相机坐标系的原点。

        已知：1）P在两个像素坐标平面的投影点p1,p2。2）p1和p2确定匹配正确。3）相机内参

        想求：相机的运动R,t（外参）

        （1）补充知识

        1）相机坐标系-像素坐标系

         2）关于基线、极线等内容

        （2) 求解与分析过程  

•   这里的s1和s2就是深度（也就是相机坐标系下的Z），和前面像素坐标与相机坐标的变换关系是一摸一样的。
•   为什么会有RP+t，因为需要把P从第一个相机的坐标系变换到第二个相机的坐标系。

         对极约束刻画了O1，O2，P共面的关系，给出了两个匹配点（p1,p2)的空间位置关系

         我们发现E和F是相近的（因此用一个就可以），E刻画了外参矩阵，F同时刻画了外参+内参矩阵。因此E和F是求解相机运动的一个跳板，借助它们来求解R和t。

        注意，这时候E和F是3*3的矩阵！！。       

         对极几何的本质矩阵满足如下性质，这里的性质2是很重要的！

         如何进一步去理解本质矩阵只有5个自由度？

        

        因此最少可以用5对点来求解E

         （3）求E

        

        

        

         

        

        

        

        

        

        

        

        

        

        

        

        

        

        

        

         

        

        

        

        

        

               

        

        

3 立体匹配（MVS）的过程概述

        参考立体匹配概述_右边的口袋的博客-CSDN博客_mvs立体匹配

        3.1 相机标定

        大概是相当于sfm那一步，目的是获得两个相机的内参（焦距、图像中心、畸变参数等）以及外参（世界坐标系与相机坐标系之间的变换矩阵R和T），之后对图像进行校准，处理并获取图像的立体点对；

        

4 MVSNet用到的一些名词概述

        4.1 cost volume

        这个东西的目的是去匹配视差。就是视图间的点以最小的误差进行匹配。

        Cost Volume - 知乎 (zhihu.com)

        

        这个词主要是在双目视觉中，用于计算左右两幅图像的相同像素点的视差的。

        换句话说就是，我有一个点A，他在左边的摄像头的视野中在x点，在右边的摄像头的视野中在y点，那么x和y这两个像素点间的差距d就是disparity（视差）

        那么可以用如下的方法来建立disparity搜索空间。

        因为相机之间的距离是确定的，所以d一定是有个最大值D的，就可以建立起0-D的一个搜索空间（因为是像素间距离，所以可以是整数化的）。

        建立起搜索空间之后，就可以用点积的方式来得到每个d下的cost了（就是求一下相似度，结果会在0-1之间。1就表示这个视差下，就是这个像素点。这样就可以估计每个点的深度）

     

        4.2 sweep plane

        平面扫描法

三维重建之平面扫描算法（Plane-sweeping）

        用垂直于深度方向的一个个平面去确定物体上的某个点M，和不在物体上的点M’。

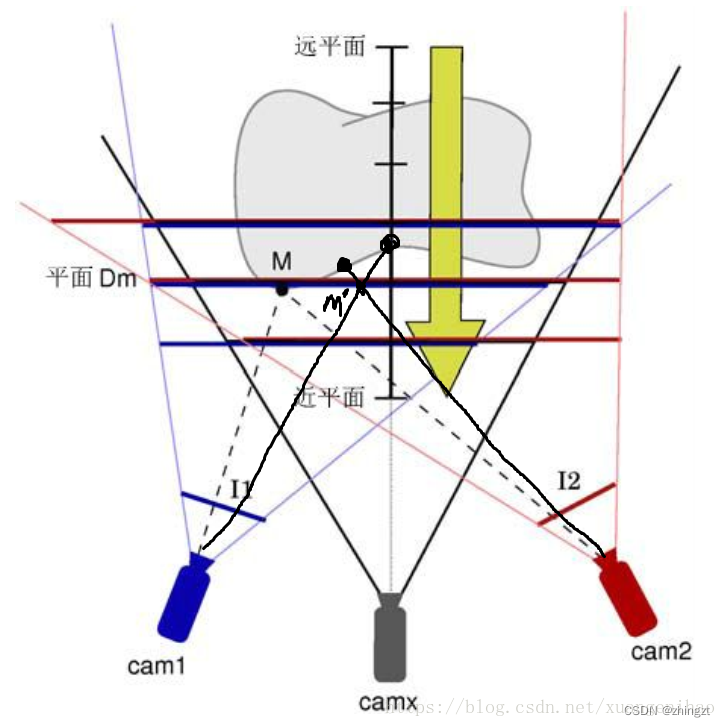
        4.3 相机标定与内参外参

        可参照此文档：相机校正与相机内参、外参

        从世界坐标系到图像（也就是一个投影关系），将按照如下关系：

             在extract feature的时候，我们将图片尺寸变为了原来的1/4，那么就认为图像缩小了1/4，所以相应的相机内参也应该缩小为1/4，变成K/4。

        也就是说内参等比例改变会影响图片尺寸。反过来说，图片等比例的改变大小，必须要同时调整内参，这样才能够保证相对应关系。

        什么是reference camera，source camera ，一张reference对应N张source camera。（1+N具体是多少是提前规定好的，一般也就3张or5张）

        4.4 单应性变换（homograph）

        所谓单应性变换就是让图像在不同的坐标系（比如世界坐标系和相机坐标系或者就是不同的相机坐标系）之间进行变换。（也有用到wrap这个词）

        前提是相机的内参和外参等等信息。

        从而让图像统一到一个坐标系下？source image和reference image的关系

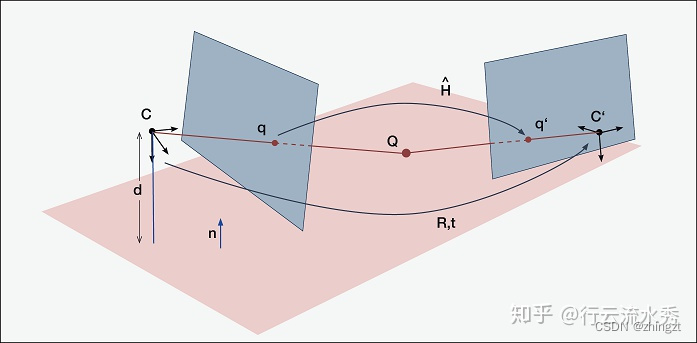
        会有这样的一个单应性变换矩阵来描述实际同一点在不同图像上的像素坐标之间的关系，也可以去描述不同的相机坐标之间的关系。

5 摄影测量的知识

        主要来源于如下内容的学习：

摄影测量概述 - 知乎 (zhihu.com)

        摄影测量：从摄影完成测量 // 由二维的像片点坐标得到对应目标的实际三维坐标，后续的应用有制图、三维重建等多种应用。

        更属于计算机图形学的内容，和计算机视觉有些不一样，但也有共性的部分。

        5.1 基本坐标系和内外方位元素

        像平面坐标系 vs 像素坐标系(图像坐标系）

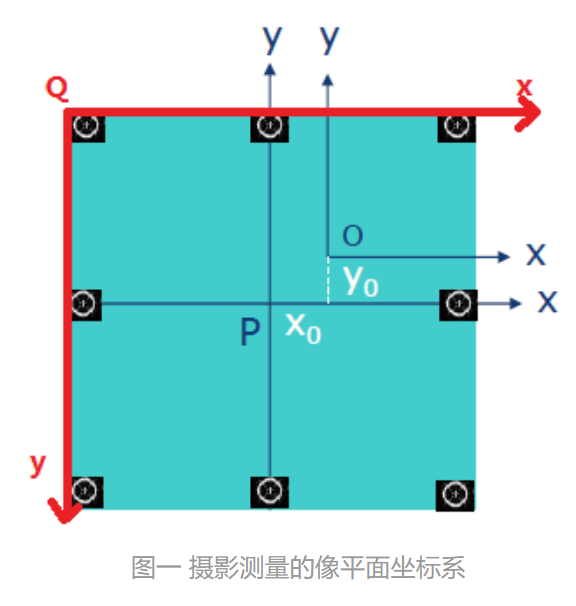
        1）世界坐标系（D-XYZ 摄影测量物方坐标系，和实际大地测量坐标系可以相互转化）旋转+平移，六个外方位元素 - 2）相机坐标系 - fx,fy 3）像平面坐标系 - x0,y04）像素 (图像) 坐标系

        

         下面这个图非常重要！！！！中间的S-uvw由于是摄影测量的辅助坐标系，可以先撇开不管，像框标坐标系也可以不管。其余必须记住！！！

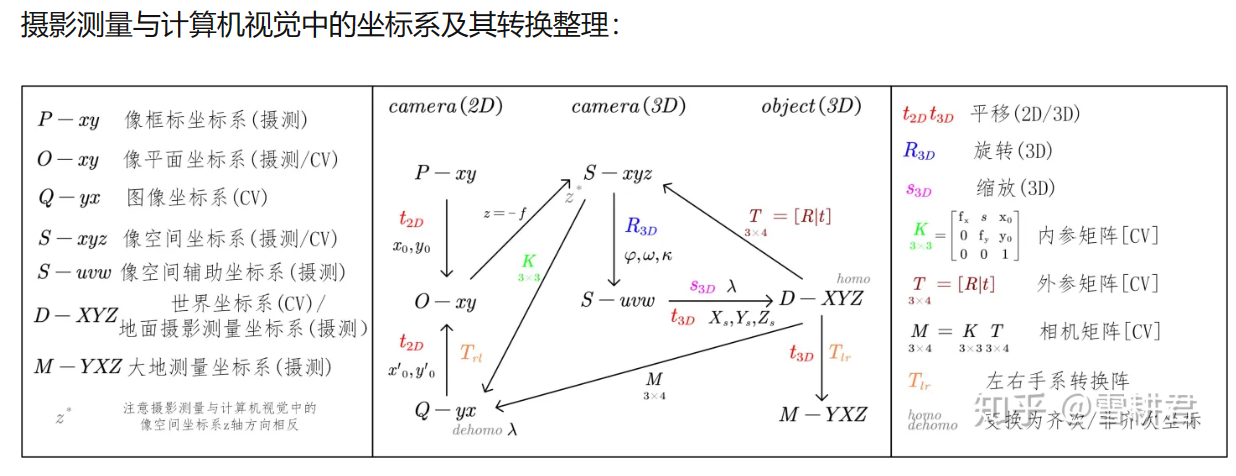
         5.2 共线方程，后方交会，前方交会

        由于我们希望物体不会倒立，那么就认为成像平面是在相机和物体之间的。

        此外，S-相机光心，a-像点，A-物点 三点是在一条直线上的。这就是共线约束！其实就是描述了坐标系之间的变换关系。

        因此一组已知的(x,y)和(X,Y,Z）这样的控制点，就可以得到两个共线方程。

         摄影测量的外方位元素获得困难，GNSS可以得到位置，POS中的IMU可以获得姿态，但是不精确且成本较高。

        由于外参为未知数，共6个未知数，因此共需要3个控制点，能建立6个共线方程。

        这就叫后方交会（做的是镜头后方的事），目标是恢复像片拍摄时的位置和姿态。        

     

        前方交会：为了求解空间中的点，换句话说，三角测量。        

          自己的理解：当我们想知道某个地面加密点（图像上的某个点）的空间坐标（X,Y,Z)，那么总共求解3个未知数，如果已知两个相机的位姿，那只需要两张像片，相当于两对像素值，这样就得到2*2=4个共线方程。这样就可以求解实际坐标值(X, Y, Z).（其实就是联立方程求未知数的问题）.

       具体求解过程是通过迭代平差法，这对初值的依赖比较高，所以可能导致我们需要输入一定的初值来辅助解算？例如POS系统的初值。       

        所以其实两张相片就可以了！        

        5.3 补充计算机视觉中对共线方程、前方、后方的相应描述和内容：

         用一个方程来联系图像坐标系和世界坐标系。

        计算机视觉中关键的主要有三个坐标系：世界坐标系、相机坐标系、图像坐标系。

         5.3.1 齐次坐标        

         5.3.2 M的求解

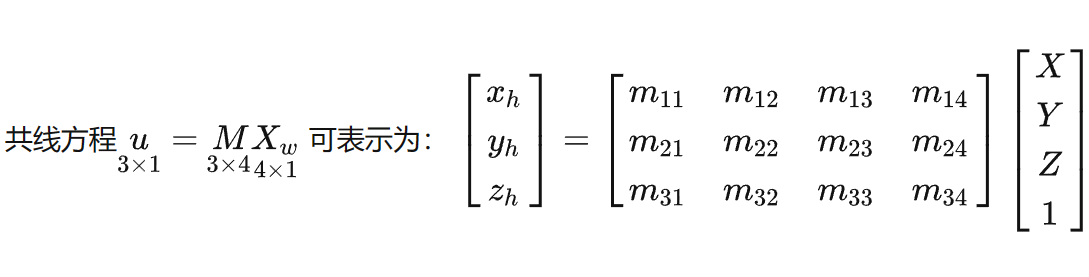
         直接线性化整理求解。

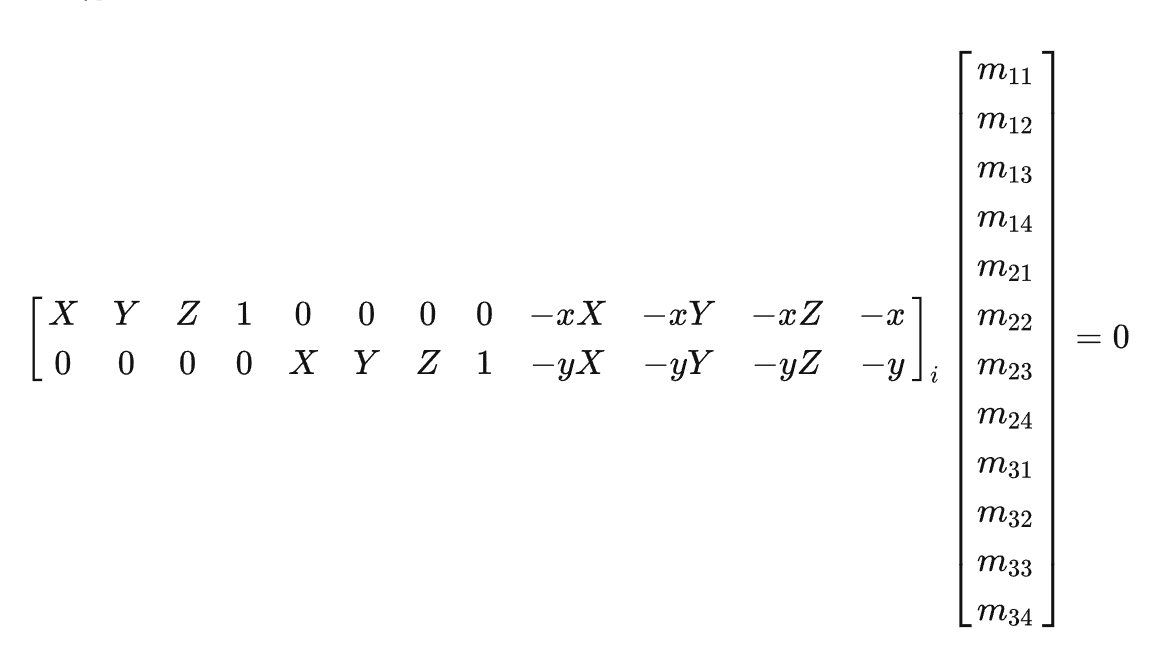
         包含奇异值分解、归一化等操作。需要尽量克服测量噪声。

        实际求解过程中，我们会通过归一化(normalization)来将 A  良性化(well-conditioned), 即将所有像点x,y ，物点X,Y,Z分别作平移缩放使得A 中元素都在一个数量级。在解算出 m 后再对 M 乘这个平移缩放变换阵得到去归一化后的  M  。这个归一化操作在CV中的各种矩阵估计里都算是个惯用的技巧。

        12个未知数，所以至少要给到6组点进行平差估计，恢复M矩阵。

        5.3.3 相机具体内外参求解

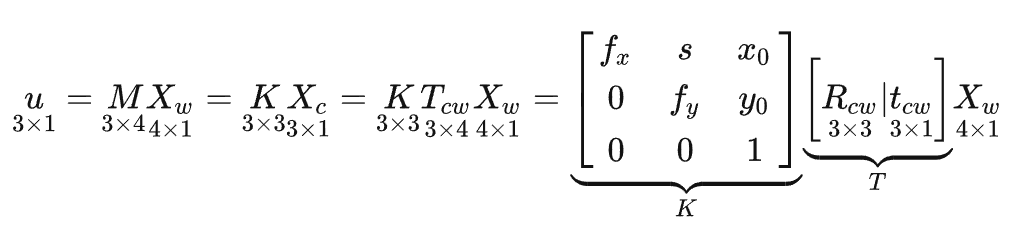
         对于内参矩阵中的s，摄影测量中一般认为s = 0（所谓的错切参数），且fx = fy = f，xy尺度相同。

        但是如果啥都不管，K有5个，T有6个，11个独立参数，这与M的自由度是一致的。因为共线方程在齐次坐标下表示是去尺度的（所以从12个自由度要减1个） 

         从M中分解出K,R,t

        相机标定 - 仅知道像方和物方点坐标，求解相机内参。

        用如下的相机标定棋盘可以来进行标定。

        

         知二得一。

        5.3 共面方程，相对定向，绝对定向（对极几何）

        如果我们不知道相机外参，还是想做前方交会呢？所以可能需要同时估计相机外参和前方摄影测量点，这时候未知数就会多很多，怎么解决呢？

        5.3.1 摄影测量中的概念

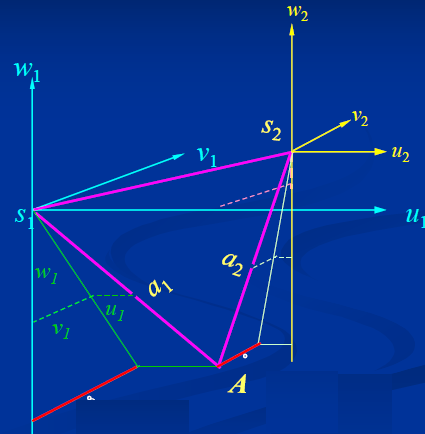
        同名像点：对应于同一个物点的不同图上的像点

        同名光线：光心到同名像点的射线。（同名光线理论上交于物点）

        摄影基线：相机中心S1和S2的连线。

        故有S1A，S2A和S1S2三条线共面。

         

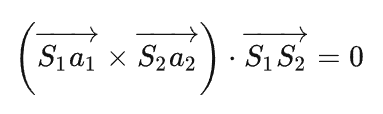
         bu，bv，bw就是光心之间的相对坐标。

        所谓的像点就是a1和a2

        所以建立了一个非常简单的共面方程。

        都是在像空间辅助坐标系下，换句话说方向都是相同的，只存在平移问题。

        又因为像空间辅助坐标系可以和相机坐标系（相机坐标系下的坐标就可以用像素坐标和内参来表示）关联，其中存在旋转矩阵的关系。

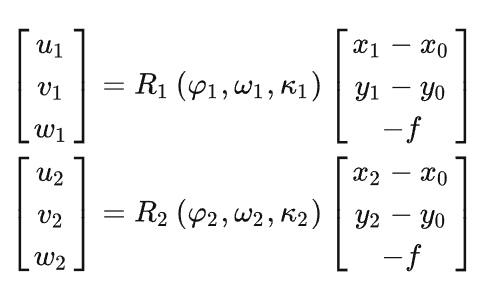
         连续像对相对定向：

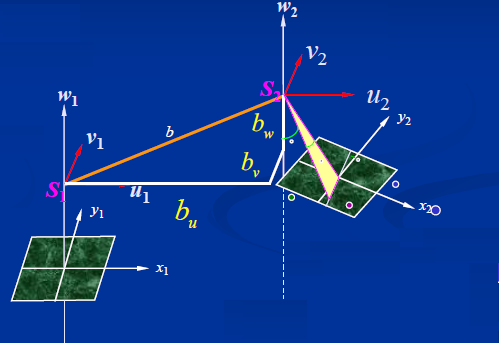
         固定左像片，基于同名光线两两相交的原理，去确定右像片的方位姿态。所以说是一种相对的概念。

        我们可以随便设左像片的旋转矩阵（反正是相对的，所以也不是很重要），此时u1，v1，w1可以通过相机自己的方程来求（就是从相机坐标系变换出来）。

        右像片的旋转矩阵是未知的，u2，v2，w2可以由旋转矩阵确定。

        同时bu，bv，bw不考虑尺度的话，确定两个就行了，只要知道相互之间的比例即可。

        所以五个未知数就可以构成相对定向参数。

        这样就可以在空间中构建一个没有尺度的三角形，自由度为5.