【算法】交换排序 选择排序 （冒泡排序 快速排序 单趟排序（Hoare大佬法） 单趟排序（挖坑法） 单趟排序（前后指针法））（直接选择排序 堆排序）_void selectsort(s16 *a,s16 n)

---

选择排序

思想

从要排序的元素中选出最小的然后存放在序列的起始位置，直到所有的元素排完。

我们可以优化一下，我们选两个数，我们可以选出最小的也可以选出最大的。把两个数一起选出来最小的扔左边，最大的扔右边。

需要注意的是我们不能选出最大和最小的数，我们是要选出最大和最小数的位置（下标）。

直接选择排序

void SelectSort(int* a, int n)
{
	int begin = 0;
	int end = n - 1;
	while (begin < end)
	{
		//选出最小的放begin位置
		//选出最大的放end位置
		int mini = begin, maxi = begin;
		for (int i = begin + 1; i <= end; ++i)
		{
			if (a[i] > a[maxi])
			{
				maxi = i;
			}

			if (a[i] < a[mini])
			{
				mini = i;
			}
		}

		Swap(&a[begin], &a[mini]);
		if (maxi == begin)
		{
			maxi = mini;
		}

		Swap(&a[end], &a[maxi]);
		++begin;
		--end;
	}
}


void TestShellSort()
{
	int a[] = {9,8,7,6,5,4,3,2,1,0};
	ShellSort(a, sizeof(a) / sizeof(int));
	PrintArray(a, sizeof(a) / sizeof(int));
}


int main()
{
	TestSelectSort();
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

最坏时间复杂度：O(N²)
最好时间复杂度：O((N²)]

堆排序

利用堆删除思想来进行排序

int a[] = {20，17，4，16，5，3}; 
1

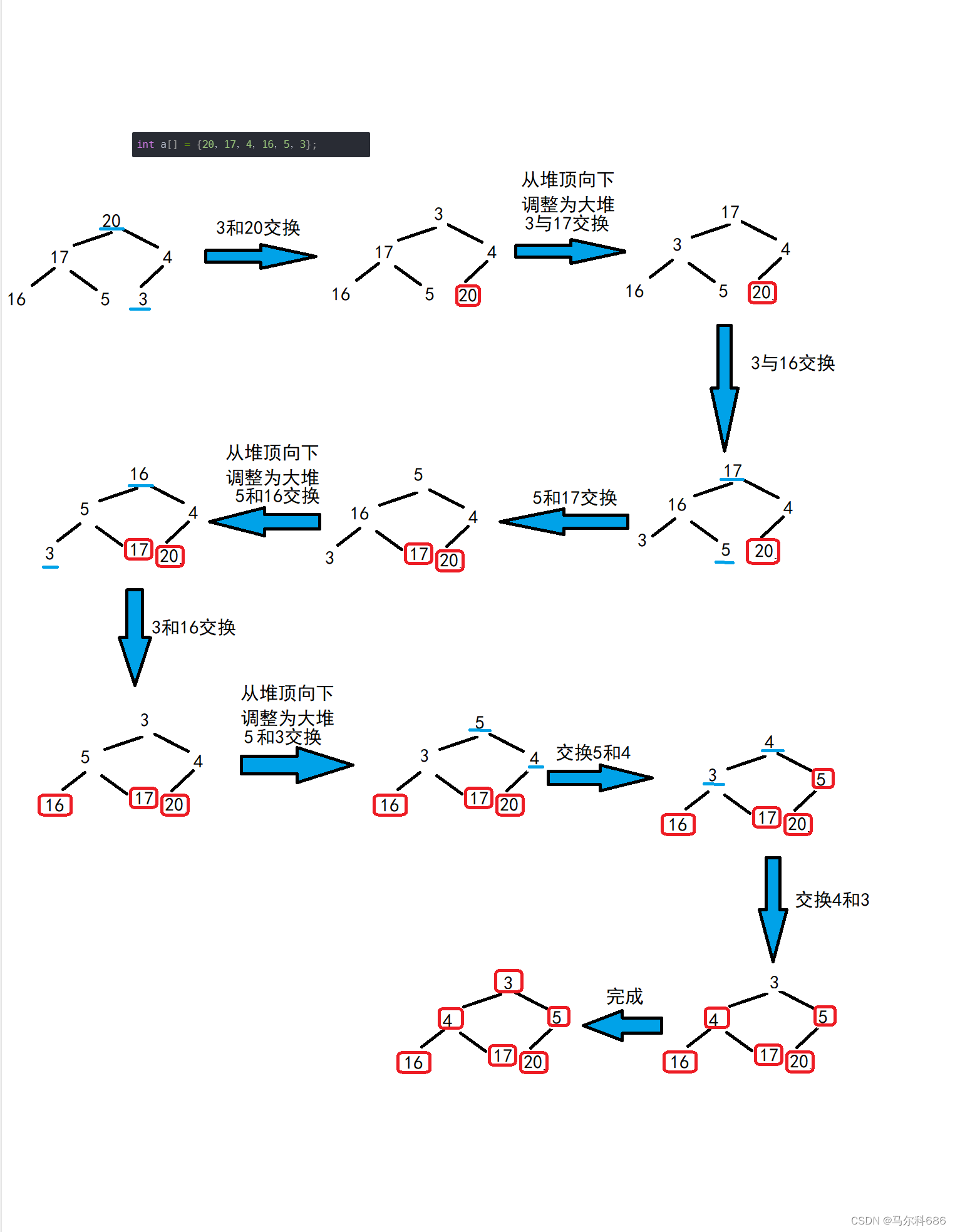
void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void AdjustDown(int* a, int n, int parent)
{
	int minChild = parent * 2 + 1;
	while (minChild < n)
	{
		// 找出小的那个孩子
		if (minChild + 1 < n && a[minChild + 1] > a[minChild])
		{
			minChild++;
		}

		if (a[minChild] > a[parent])
		{
			Swap(&a[minChild], &a[parent]);
			parent = minChild;
			minChild = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
// O(N*logN)
void HeapSort(int* a, int n)
{
	// 大思路：选择排序，依次选数，从后往前排
	// 升序 -- 大堆
	// 降序 -- 小堆
	// 建堆 -- 向下调整建堆 - O(N)
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDown(a, n, i);
	}

	// 选数
	int i = 1;
	while (i < n)
	{
		Swap(&a[0], &a[n - i]);
		AdjustDown(a, n - i, 0);
		++i;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

交换排序

基本思想：所谓交换，就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置，交换排序的特点是：将键值较大的记录向序列的尾部移动，键值较小的记录向序列的前部移动。

冒泡排序

1. 冒泡排序是一种非常容易理解的排序
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：稳定

void BubbleSort(int* a, int n)
{
	for (int j = 0; j < n; ++j)
	{
		int exchange = 0;
		for (int i = 1; i < n - j; ++i)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				exchange = 1;
			}
		}
		if (exchange == 0)
		{
			break;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

最坏时间复杂度：O(N²)
最好时间复杂度：O((N)]

快速排序

Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

单趟排序（Hoare大佬法）

单趟排序:

1. 选一个key。（一般是第一个或者是最后一个）
2. 单趟排序，要求小的在key的左边，大的在key的右边。

Hoare大佬的方法：

相遇位置如何保证比key小：

左边第一个值做key，R先走。
分析：

1. R先走，停下来了，L撞到R，相遇位置比key小。
2. L停下来，R撞到L，相遇位置比key小。
3. 同样道理右边第一个值做key，L先走。

单趟排序的价值：
4. key已经到了它的最终位置，就不用动了。
5. 分割出两个子区间。如果子区间有序，整体就有序了。

快排的递归深度为：logN（每次key都是中位数）
时间复杂度：O(N*logN)

当有序/接近有序的时候快排的效果就很坏，此时时间复杂度为：O(N²)

优化1：

1. 随机选一个位置做key。
2. 针对有序，选正中间值做key。
3. 三数取中。

int GetMidIndex(int* a, int left, int right)
{
	int mid = left + (right - left) / 2;
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else if (a[left] > a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else // a[left] >= a[mid]
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else if (a[left] < a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

优化2：小区间优化

1. 小数据量用插入排序，大数据量用快排，可以减少递归调用次数。

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}

	if (end-begin <= 8)
	{
		InsertSort(a + begin, end - begin + 1); 
	}
	else
	{
		int keyi = PartSort(a, begin, end);
		//[begin,keyi-1] keyi [keyi,end]
		QuickSort(a, begin, keyi - 1);
		QuickSort(a, keyi + 1, end);
	}


}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

整体代码：

int GetMidIndex(int* a, int left, int right)
{
	int mid = left + (right - left) / 2;
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else if (a[left] > a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else // a[left] >= a[mid]
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else if (a[left] < a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}
//单趟排序(Hoare大佬法)
//[left,right]
int PartSort(int* a, int left, int right)
{
	// 三数取中
	int mid = GetMidIndex(a, left, right);
	Swap(&a[left], &a[mid]);

	int keyi = left;
	while (left < right)
	{
		//让R先找小
		while (left < right && a[right] >= a[keyi])
		{
			--right;
		}
		//L找大
		while (left < right && a[left] <= a[keyi])
		{
			++left;
		}
		if (left < right)
		{
			Swap(&a[left], &a[right]);
		}
	}
	int meeti = left;
	Swap(&a[meeti], &a[keyi]);
	return meeti;
}

//[left,right]
void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	int keyi = PartSort(a, begin, end);
	//[begin,keyi-1] keyi [keyi,end]
	QuickSort(a, begin,keyi - 1);
	QuickSort(a, keyi + 1, end);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

---

单趟排序（挖坑法）

右边先走找小填左边的坑，左边后走找大填右边的坑。

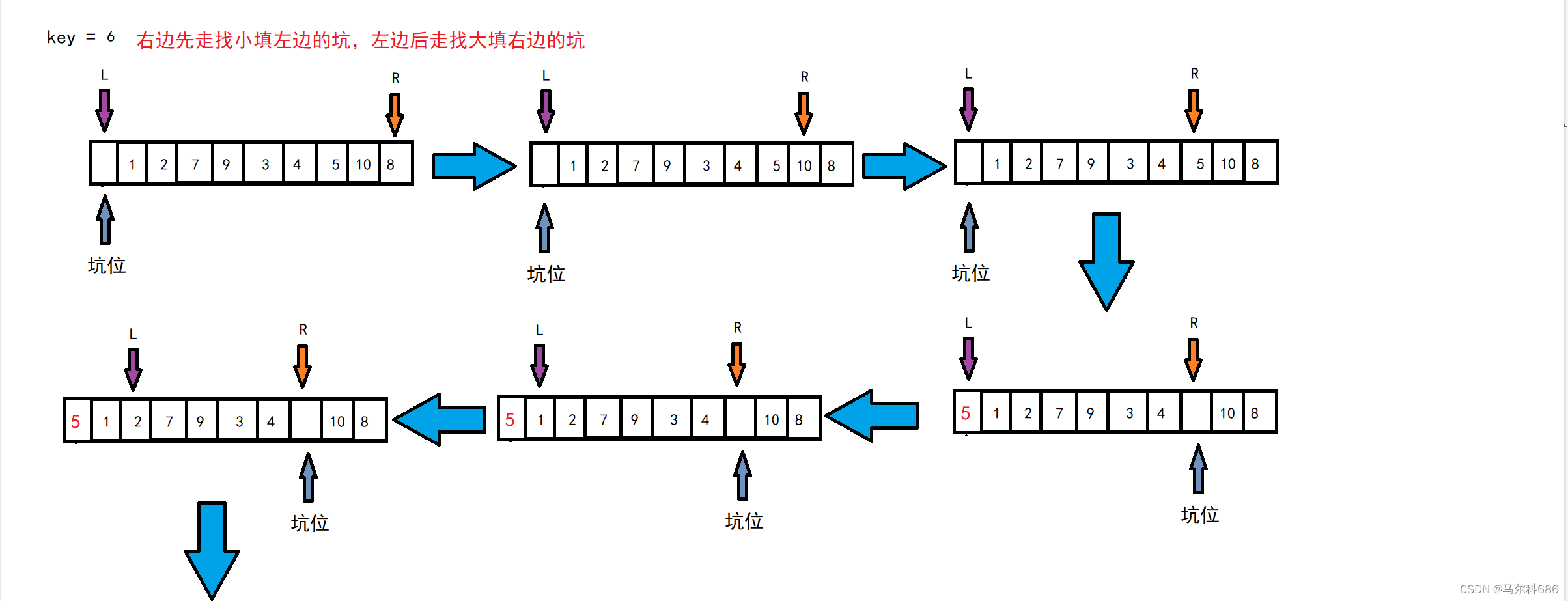
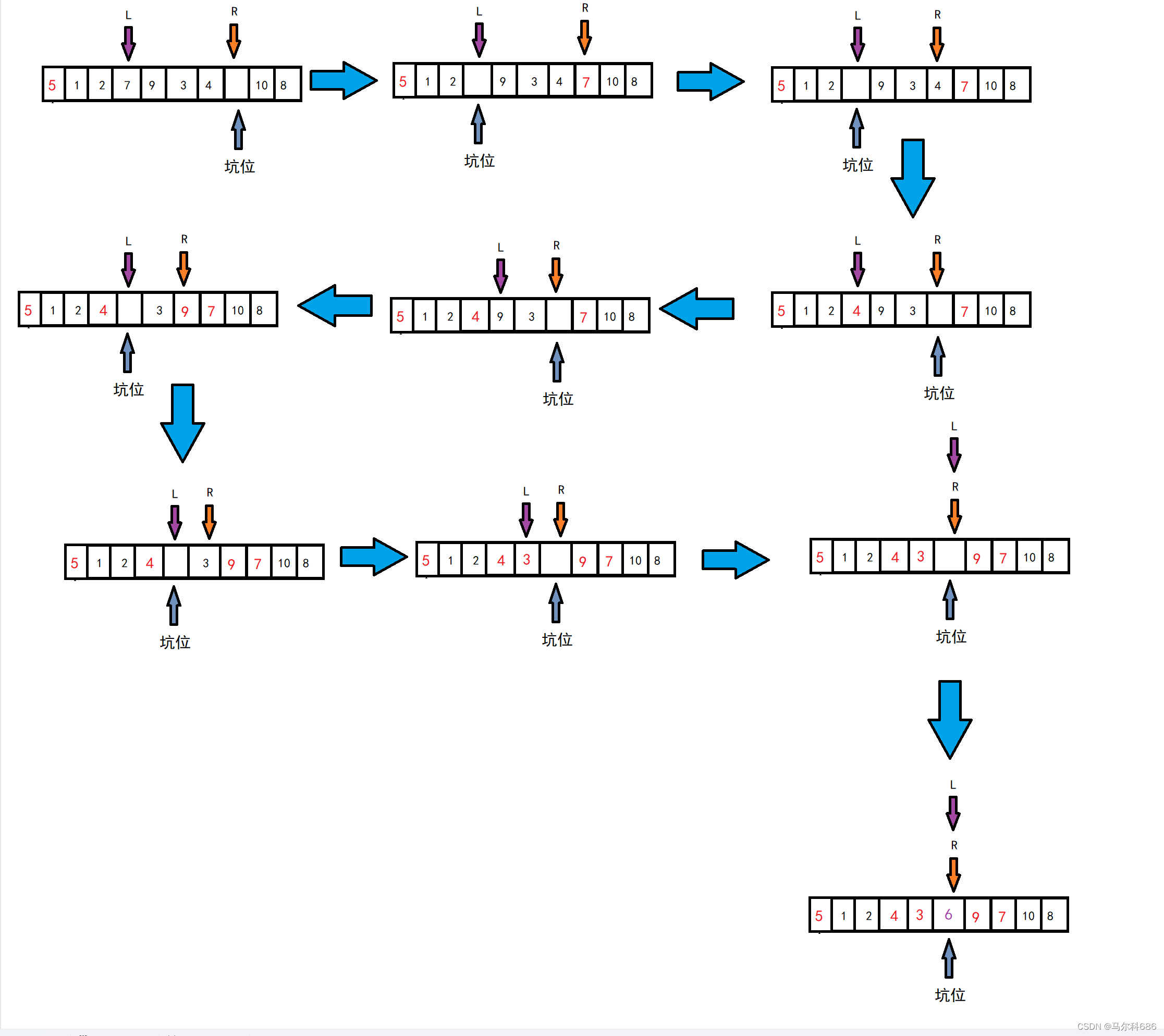
//挖坑
int PartSort2(int* a, int left, int right)
{
	// 三数取中
	int mid = GetMidIndex(a, left, right);
	Swap(&a[left], &a[mid]);

	int key = left;
	int hole = left;
	while (left < right)
	{
		//右边找小填左边的坑
		while (left < right && a[right] >= key)
		{
			--right;
		}
		a[hole] = a[right];
		hole = right;

		//左边找大填右边的坑
		while (left < right && a[left] <= key)
		{
			++left;
		}
		a[hole] = a[left];
		hole = left;
	}
	a[hole] = key;
	return hole;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

单趟排序（前后指针法）

初始时，prev指针指向序列开头，cur指针指向prev指针的后一个位置。
cur找小，prev的两种状态：a.紧跟着cur、b.在比key大的值前面

cur指针指向的数据小于key，prev先后移一位，然后与cur指向的数据交换，cut再++。
整体就是把大的值往右边推，把小的值往左边翻。

实现：

cur遇到比key大的往后走，遇到比key小的就停下来，++prev，交换prev和cur位置的值。

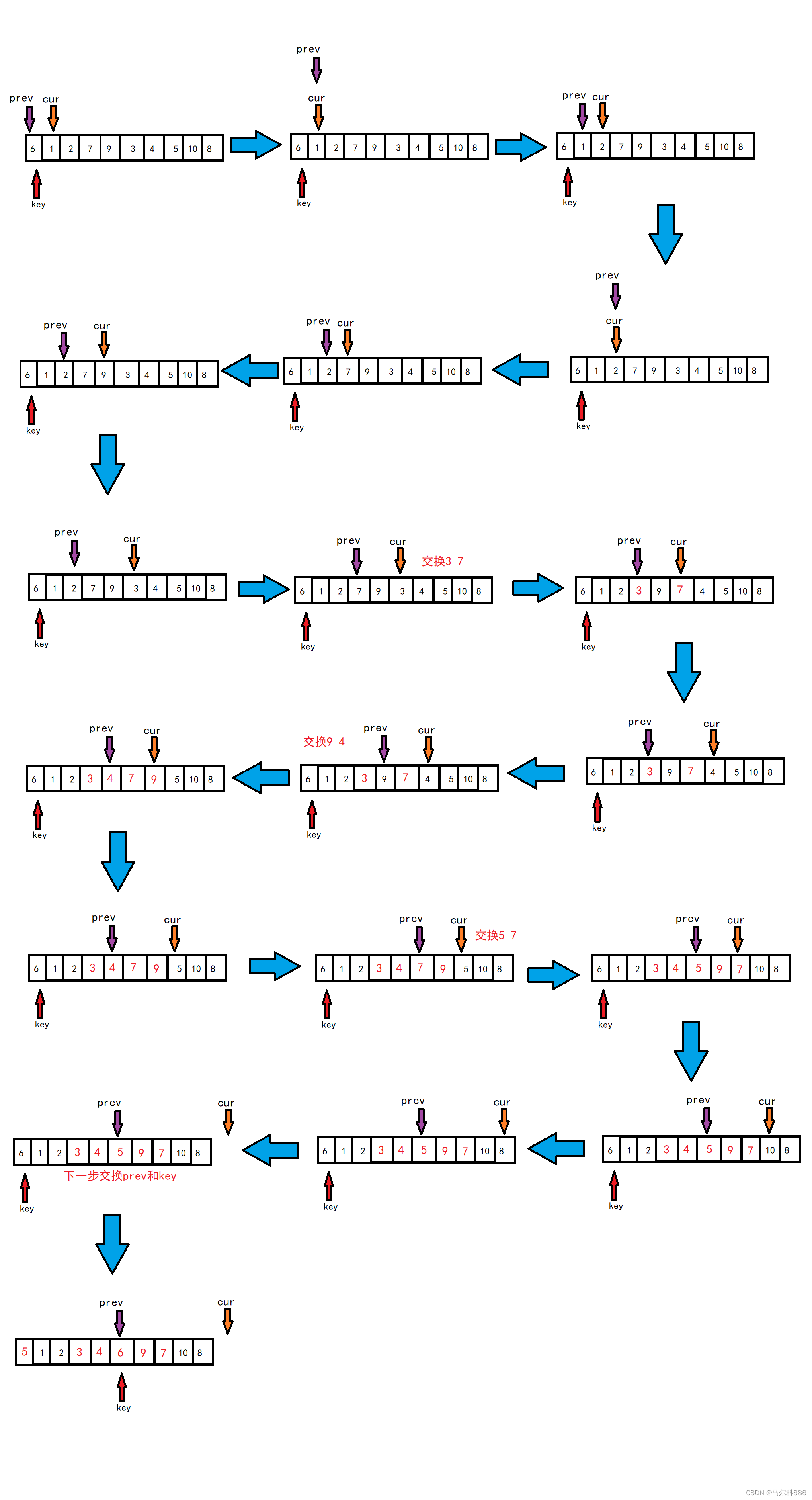
代码：

//前后指针法
int PartSort3(int* a, int left, int right)
{
	// 三数取中
	int mid = GetMidIndex(a, left, right);
	Swap(&a[left], &a[mid]);

	int prev = left;
	int cur = left + 1;
	int keyi = left;
	while (cur <= right)
	{
		if (a[cur] < a[keyi] && ++prev != cur)
		{
			Swap(&a[cur], &a[prev]);
		}
		++cur;
	}
	Swap(&a[keyi], &a[prev]);

	return prev;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23