scipy之数据插值详解_scipy插值

数据插值

插值：在离散数据的基础上补差连续函数，使得这条曲线完全通过所有的离散数据。插值是离散函数逼近的重要方法，利用它可以通过函数在有限个点处的取值情况，估算出函数在其它点的取值。

与插值另一个密切相关的是问题是如何来通过简单函数逼近复杂函数，对于离散的数据点，想要使得曲线能够通过这些点的算法也是多种多样的，这就取决使用的插值算法，插值算法主要包括下面几种类型：

• 片段插值
  片段插值是最简单的插值算法，通过给最近的数据分配相同的值，也被称为最近邻插值。
  
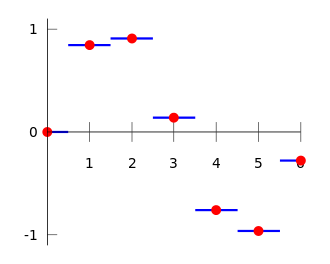
• 线性插值
  线性插值由线性函数组成，是快速且简单的插值算法，但不是精确的，而且在转折的插值点是不可微分的。
  
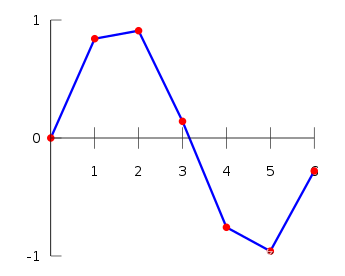
• 多项式插值
  多项式插值是线性插值的推广，线性插值是由线性函数组成，而多项式插值是由来代替的。
  
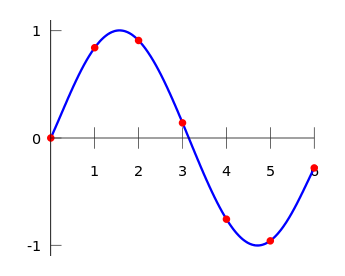
• 样条曲线插值
  样条插值在每个间隔内使用低阶多项式，并使用多项式以使得它们能够平滑吻合的连接在一起。
• 三角内插
• 有理内插
• 小波内插

下面我们使用scipy基于上面几种插值的情况来进行介绍，scipy中插值主要分为以下几种类型：

• 1维的数据插值
• 多元的数据插值
• 样条插值
• 使用径向基函数进行平滑的插值

1维的数据插值

在scipy中1维的数据插值算法被封装在interp1d 方法中，利用给定的数据点，使用不同的插值算法来预测区间内其它数据点的值。
参数：

• x：数据点输入的值
• y：数据点输出的值
• kind：设置使用的插值算法，参数的取值有：linear, nearest, nearest-up, zero, slinear, quadratic, cubic, previous
• axis：指定使用y中的那个轴作为插值的输出数据，默认使用最后一个轴
• copy：是否要重新开辟保存数据的内存块，默认是重新开辟空间的
• bounds_error：对于超出x的取值范围是否抛出错误，默认是抛出错误的，如果设置为False就会使用fill_value参数设置的值来进行填充
• fill_value：设置填充值
• assume_sorted：设置x是否需要按照顺序

import numpy as np
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt


#用于计算插值函数使用到的数据点
x = np.linspace(0,2*np.pi,4)
y = np.sin(x)
#用于插值函数进行预测的数据点
x_all = np.linspace(0,2*np.pi,20)
y_all = np.sin(x_all)
#绘制插值使用的数据点
# plt.plot(x,y,color="r",marker="o")
#绘制真实的曲线
plt.plot(x_all,y_all,color="r",linestyle="-")
#设置使用的插值算法
kind_list = ["linear","cubic","quadratic","nearest"]
#设置线的类型
line_type_list = [":","-.","--",":"]
#设置线的颜色
line_color_list = ["g","b","k","y"]
for i,kind in enumerate(kind_list):
    #使用线性插值来计算函数
    f = interp1d(x,y,kind=kind)
    #使用插值函数来计算其他点的取值
    f_y = f(x_all)
    #绘制曲线
    plt.plot(x_all,f_y,color=line_color_list[i],linestyle=line_type_list[i])

#添加图例
plt.legend(["data","linear","cubic","quadratic","nearest"], loc='best')

plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

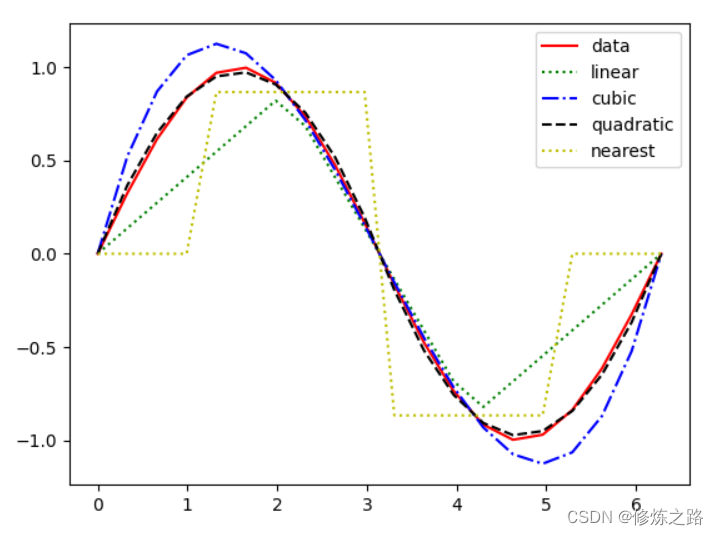
我们使用interp1d 实现了几种不同的插值算法，有兴趣的同学可以尝试另外几种插值算法的效果，在使用插值算法利用离散点来计算函数的时候我们只使用了4个点，然后再用函数来预测20个点的取值，使得绘制的曲线能够更加平滑，以便我们更好的观察不同插值算法的效果。

data表示的是实际的曲线，所以如果与红色曲线吻合的越好说明插值算法的效果越好，拟合函数的误差更小，从下图来看，quadratic插值算法的效果最好。这并不能说明quadrati插值算法的效果，一定会好于其他的插值算法，主要还是需要根据使用场景以及曲线。

多元的数据插值

多元的数据中的元其实指的是变量，也就是说函数的变量有多个，对于2维及以上维度的数据，都是以grid的形式来存储数据。在scipy中提供了griddata方法专门来针对高维的数据进行插值计算
参数：

• points：输入数据点
• values：数据点对应的值
• xi：插入的数据点，也就是需要预测值的数据点
• method ：使用的插值算法linear, nearest, cubic
• fill_value：用于填充输入数据点外的值，默认使用nan，这个值对于nearest插值算法没有影响
• rescale：在执行插值前将数据点缩放到单元立方体

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import griddata

def fun(x,y):
    """定义一个2元函数
    :param x:
    :param y:
    :return:
    """
    return x*(1-x)*np.cos(4*np.pi*x) * np.sin(4*np.pi*y**2)**2

#x从0到1取100个值,y从0到1取200个值组合作为预测的数据点
#最终返回的值是按照grid的形式返回的
grid_x,grid_y = np.mgrid[0:1:100j,0:1:200j]

#随机获取1000个点
rng = np.random.default_rng()
points = rng.random((1000,2))
#获取点的取值
values = fun(points[:,0],points[:,1])
method_list = ["nearest","linear","cubic"]
localtion_list = [222,223,224]

plt.subplot(221)
plt.imshow(fun(grid_x,grid_y).T,extent=(0,1,0,1),origin="lower")
#k.绘制黑色的数据点
plt.plot(points[:,0],points[:,1],"k.",ms=1)
plt.title("Original")

for i,method in enumerate(method_list):
    #利用不同的插值算法来获取预测数据点的结果
    grid_z = griddata(points,values,(grid_x,grid_y),method=method)
    #以图片的形式绘制数据点的结果,因为是3D只能通过图片形式来展示结果
    plt.subplot(localtion_list[i])
    #绘制不同插值算法预测结果
    plt.imshow(grid_z.T,extent=(0,1,0,1),origin="lower")
    plt.title(method)

#调整每张子图的大小
plt.gcf().set_size_inches(6,6)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

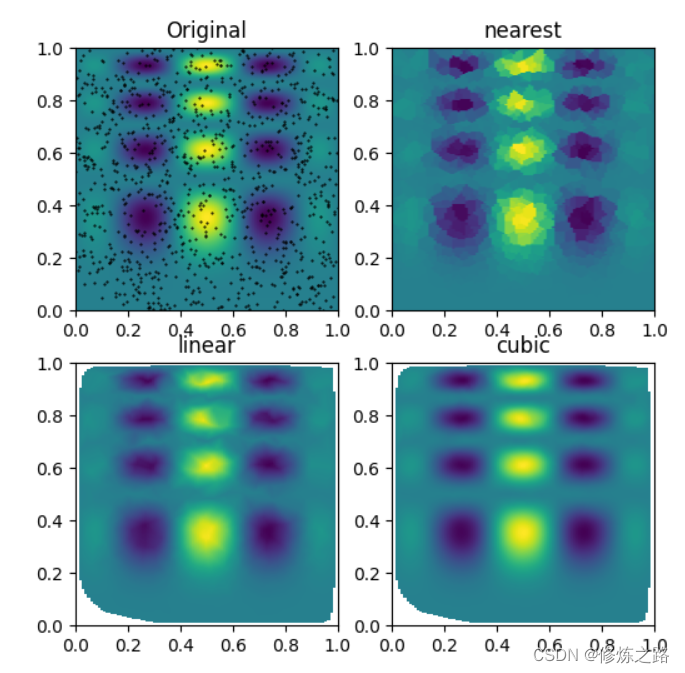
Original展示的是原函数的取值，黑色的点表示的是插值算法所使用的数据点，从下图来看cubic插值算法的结果与原函数取值更加接近。

样条插值

样条插值需要两个基本的步骤：

1. 计算样条表示的曲线
2. 使用样条去计算需要预测数据点的值

import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate

x = np.arange(0,2*np.pi+np.pi/4,2*np.pi/8)
y = np.sin(x)
#计算样条表示的参数
tck = interpolate.splrep(x,y,s=0)
#需要预测的数据点
xnew = np.arange(0,2*np.pi,np.pi/50)
#使用样条来预测数据点的值
ynew = interpolate.splev(xnew,tck,der=0)

plt.figure()
#绘制插值函数
plt.plot(x,y,"o",xnew,ynew,"--",xnew,np.sin(xnew),"-",x,y,"-.")
plt.legend(["Liner","Cubic Spline","data"])
plt.axis([-0.05,6.33,-1.05,1.05])
plt.title("Cubic-spline interpolation")
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

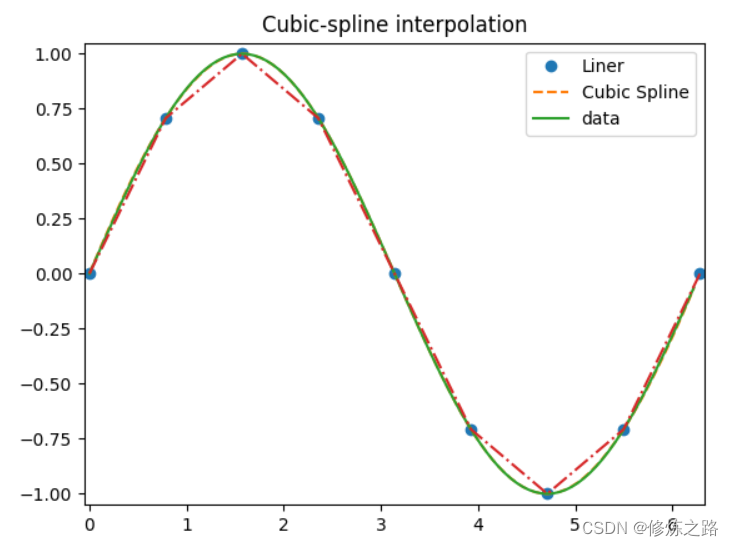
使用径向基函数进行插值

径向基函数可以用于N维离散数据的平滑/插值，但是对于观测数据点范围外的数据应该谨慎使用

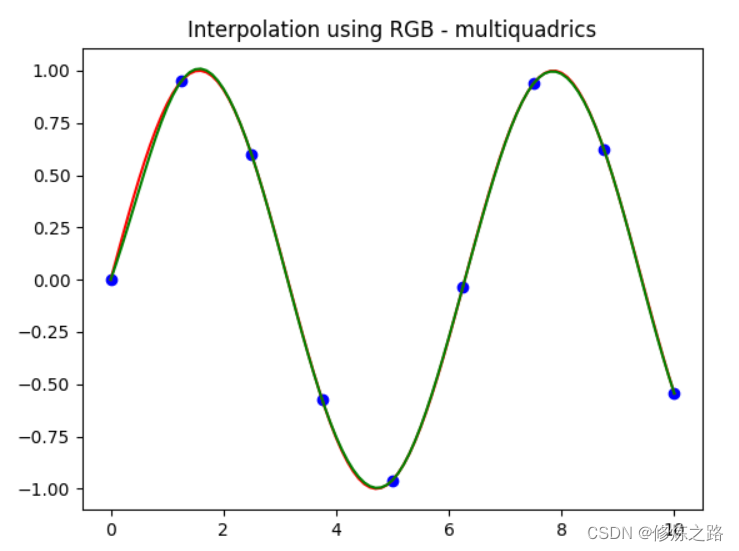
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import Rbf,InterpolatedUnivariateSpline

#插值使用的数据点
x = np.linspace(0,10,9)
y = np.sin(x)
#预测值用到的数据点
xi = np.linspace(0,10,101)

#使用RBF函数进行插值
rbf = Rbf(x,y)
fi = rbf(xi)
#绘制数据点
plt.plot(x,y,"bo")
#绘制原函数的曲线
plt.plot(xi,np.sin(xi),"r")
#绘制插值的曲线
plt.plot(xi,fi,"g")
plt.title("Interpolation using RGB - multiquadrics")
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

通过下图不难发现，绿色的曲线(RBF插值函数预测的曲线)与红色的曲线(原函数)基本上是重合的，说明RBF插值函数的预测值与原函数的值基本上都是一致的。