热门标签
热门文章
- 1gitlab配置ssh自用精简步骤_gitlab查看ssh配置
- 2ssh内网穿透失败_usr/bin/ssh-copy-id: error: ssh: connect to host 1
- 3教程|幻兽帕鲁服务器数据备份与恢复_帕鲁 linux
- 410种常用的分析模型 数据分析必看
- 5ssh localhost免密登录
- 6anaconda_conda init bash
- 73 python pandas_python3 pandas
- 8美狐讲堂:视频用直播用SDK盘点_aliplayer和ijkplayer
- 9DHCP自动获取IP地址实验(思科)
- 10Pycharm踩坑路_win11无法启动pychar2023
当前位置: article > 正文
现代信号处理-现代功率谱密度估计AR模型_现代功率谱估计方法
作者:盐析白兔 | 2024-03-02 22:11:07
赞
踩
现代功率谱估计方法
前言
本栏前两节经典谱估计中提到:经典谱估计下,方差和分辨率是一对矛盾。这是因为经典谱估计将数据进行了加窗,自相关法还对自相关进行了加窗(二次加窗),这就让我们想到把原始数据藏在一个系统H(Z)中,让这个系统包含这组数据的特性,这样一来,系统中的系数就可以表示系统反映的数据。这就是现代功率谱密度估计-参数模型法的思想。按照书本的就是先根据数据的自相关函数r(m)求出H(Z)系数,再通过H(Z)进行谱估计。
参数模型法有AR,MA,ARMA模型,其性质为:
| AR | MA | ARMA | |
|---|---|---|---|
| H(Z) |  | 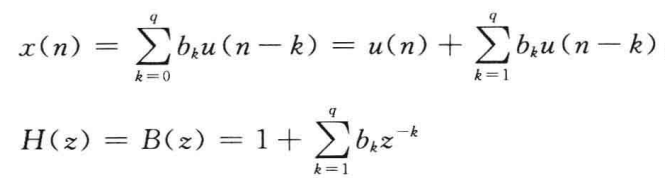 | 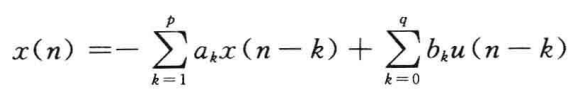 |
| 线性/非线性 | 线性 | 非线性 | 非线性 |
| 反映频谱特性 | 峰值 | 谷值 | 兼顾 |
一、概率梳理
由于AR模型是线性方程,也可以等效预测模型,所以AR模型远比另外两种实用,所以本文只梳理和仿真了AR模型。
首先模型中令输入是白噪声,需要求解H(Z)的系数也就是ak,k=1,2…p。也就是要通过数据的自相关与ak的关系进行求解,也就是需要通过正则方程(Yule-Walker方程),正则方差的推导过程如下:

其中,正则方差可以用Lecinson-Durbin递推快速算法计算,也就是自相关法的方法。后面还会说其他的方法以及比较。
并且在预测模型中,二者系统的系数是相等的,其最小误差等效于AR模型输入端白噪声的方差。其关系如下:

二、AR模型的几种方法
比较常见的有刚刚提及的自相关法,还有burg法和改进后的协方差法,它们之间的区别如下:
| 自相关法 | burg法 | 改进后的协方差法 | |
|---|---|---|---|
| 预测方式 | 前向预测 | 前后向预测 | 前向预测 |
| 加窗 | 前后加窗 | 前后都不加窗 | 前后都不加窗 |
| Levinson递推算法 | 可以使用 | 可以使用 | 不可使用 |
除此之外,还有常会用到的最大熵谱估计,由于数据可能相对于原始数据还是有截短。之前的经典谱估计是将两边直接为零,而这里是将两边加上最随机的数,也就是最大熵的准则。
三、AR模型的方法与具体仿真
为了和经典功率谱估计比较,采用的原数据和前两节经典功率谱估计一样的,仿真采取的阶数均为50
%%现代功率谱估计的一些方法 clear all; clc;close all;clear; N=200; Nfft=20000; Fs=1; n=0:N-1; x=cos(0.3*pi*n)+cos(0.32*pi*n)+0.1*randn(size(n)); fn=-0.5:2/N:0.5; figure; %% burg法 % 使用 Burg 算法得到功率谱估计; xpsd=pburg(x,50,N); pmax=max(xpsd); xpsd=xpsd/pmax; xpsd=10*log10(xpsd+0.000001); subplot(221); plot(fn,fftshift(xpsd));grid on;title('burg法'); %% 协方差法 xpsd=pcov(x,50,N); pmax=max(xpsd); xpsd=xpsd/pmax; xpsd=10*log10(xpsd+0.000001); subplot(222); plot(fn,fftshift(xpsd));grid on;title('协方差法'); %% 协方差的改进法 xpsd=pmcov(x,50,N); pmax=max(xpsd); xpsd=xpsd/pmax; xpsd=10*log10(xpsd+0.000001); subplot(223); plot(fn,fftshift(xpsd));grid on;title('改进的协方差法'); %% 最大熵法 xpsd=pmem(x,50,N); pmax=max(xpsd); xpsd=xpsd/pmax; xpsd=10*log10(xpsd+0.000001); subplot(224); plot(fn,fftshift(xpsd));grid on;title('最大熵法'); %% 自相关 figure; % 使用自相关矩阵分解的 MUSIC 算法得到功率谱估计; xpsd=pmusic(x',50,N); pmax=max(xpsd); xpsd=xpsd/pmax; xpsd=10*log10(xpsd+0.000001); subplot(311); plot(fn,fftshift(xpsd));grid on;title('自相关矩阵分解的MUSIC算法'); % 使用自相关矩阵分解的特征向量算法得到功率谱估计; [xpsd,F,V,E]=peig(x',50,N); pmax=max(xpsd); xpsd=xpsd/pmax; xpsd=10*log10(xpsd+0.000001); subplot(312); plot(fn,fftshift(xpsd));grid on;title('自相关矩阵分解的特征向量算法'); % 使用自相关法得到功率谱估计; xpsd=pyulear(x,50,N); pmax=max(xpsd); xpsd=xpsd/pmax; xpsd=10*log10(xpsd+0.000001); subplot(313); plot(fn,fftshift(xpsd));grid on;title('自相关法');
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59


声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/盐析白兔/article/detail/182686
推荐阅读
相关标签



