支持向量机 SVM | 非线性可分：核函数

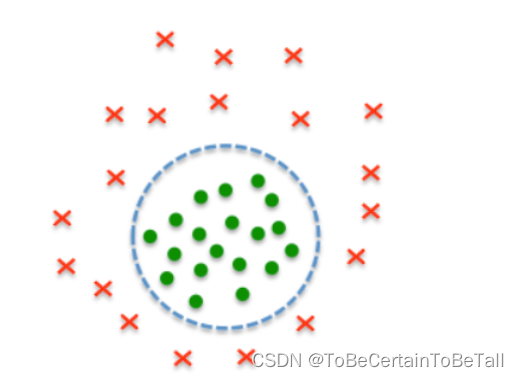
前面我们讲述了SVM算法的线性可分问题，即对应硬间隔模型和软间隔模型；下面我们来聊SVM算法的非线性可分问题

	注意：对于完全不可分的数据，SVM硬间隔与软间隔都无法解决
1

一. 情景引入

我们在线性回归：多项式扩展篇中，采用多项式扩展的方法，将低维度的数据扩展成为高维度的数据，从而使线性回归模型可以解决线性不可分的问题

以2维空间中的线性不可分为例子：
 
对于2维线性模型

$$h_{\theta }(x_1,x_2)={\theta }_0+x_1{\theta }_1+x_2{\theta }_2$$

对$(x_1,x_2)$进行2阶多项式扩展：

$$(x_1,x_2)\stackrel{多项式扩展}{\to }(x_1,x_2,x_1^2,x_2^2,x_1{x}_2)$$

对于5维线性模型

$$h_{\theta }(x_1,x_2)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_1^2+{\theta }_4{x}_2^2+{\theta }_5{x}_1{x}_2$$

那么同理，在SVM算法中，我们依然希望通过一种方法，将低维特征数据映射到高维特征数据中，从而解决数据的线性不可分问题

于是我们首先尝试通过多项式扩展的方式解决低维度到高维度映射的问题，为了描述方便，我们来定义一个$\varphi$函数，该函数的作用将数据从低维度映射到高维度中，也就是做多项式扩展；那么对于SVM优化的目标函数，我们就可以得到：
{ min ⁡ 1 2 ∑ i = 1 , i = 1 m β i β j y ( i ) y ( j ) ϕ ( x ( j ) ) ⋅ ϕ ( x ( i ) ) − ∑ i = 1 m β i s . t : ∑ i = 1 m β i y ( i ) = 0 a \left\{

$$\begin{matrix}\min\frac{1}{2}\sum_{i=1,i=1}^{m} \beta _{i}\beta _{j} y^{(i)}y^{(j)}\phi (x^{(j)})\cdot \phi( x^{(i)})-\sum_{i=1}^{m} \beta _{i} \\s.t:\sum_{i=1}^{m} \beta _{i} y^{(i)}=0 \end{matrix}$$ \right.a {min21​∑i=1,i=1m​βi​βj​y(i)y(j)ϕ(x(j))⋅ϕ(x(i))−∑i=1m​βi​s.t:∑i=1m​βi​y(i)=0​a
$$0\le {\beta }_i\le C，i=1,2,...,m$$

进一步解释$\varphi (x^{(j)})\cdot \varphi (x^{(i)})$
 
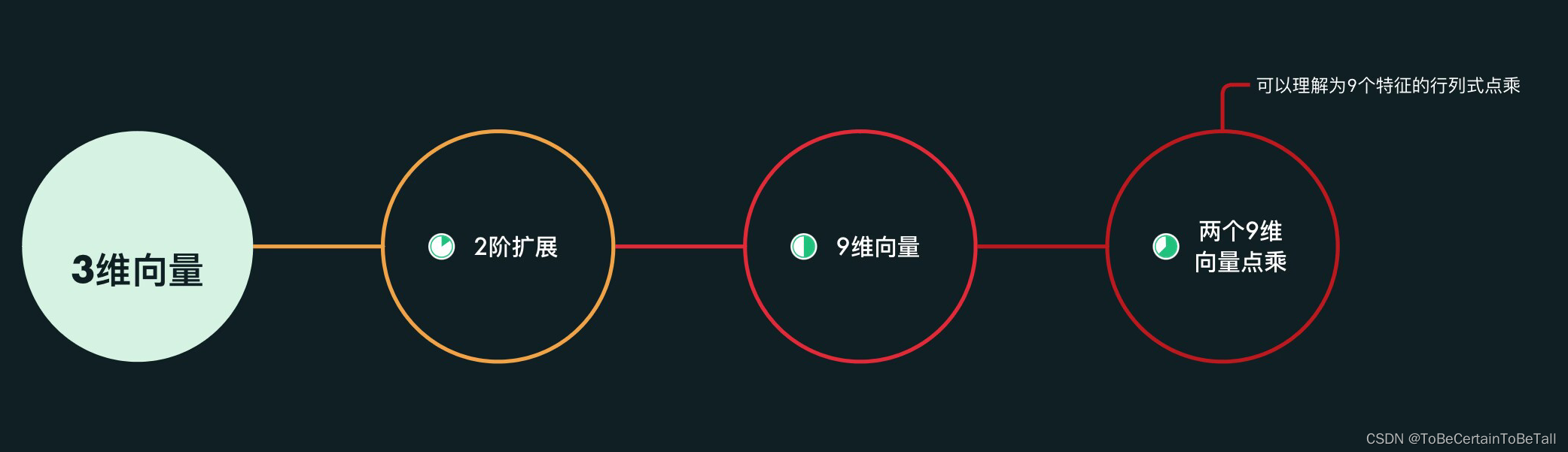
首先，明确$x^{(j)}，x^{(i)}$是向量，这里是向量的点乘
下面我们来举例子：

是不是觉得3维数据的计算量还能接受？
如果原始数据是10维，20维度，30维呢？
如果有一百万条数据呢？
显然，这样的点乘计算量巨大

二. 核函数

SVM的发明者为了解决上述计算量的问题，发明了核函数

• 核函数定义
  假设函数Ф是一个低维特征空间到高维特征空间的映射，那么如果存在函数K(x,z), 对于任意的低维特征向量x和z，都有：
  $$K(x,z)=\varphi (x)\varphi (z)$$
  则称函数K为核函数(kernal function)

• 说人话版本：
  核函数在低维空间上的计算量等价于特征做维度扩展后的点乘的结果；即核函数的作用相当于扩展后再点乘

   	这里需要补充一点
   	对于Ф(从低位映射到高维)而言，多项式扩展只是其中的一种方法
  1
  2

即，核函数用低维空间中少量的内积的计算量让模型具有高维空间中的线性可分的优点

---

首先我们用算式说明：

假设向量$x_1=({\alpha }_1,{\alpha }_2{)}^T，x_2=({\eta }_1,{\eta }_2{)}^T$

2阶扩展映射到五维空间中，我们可以得到：
$$\varphi (x_1)\cdot \varphi (x_2)={\alpha }_1{\eta }_1+{\alpha }_2{\eta }_2+{\alpha }_1^2{\eta }_1^2+{\alpha }_2^2{\eta }_2^2+{\alpha }_1{\alpha }_2{\eta }_1{\eta }_2$$
而对于K函数的思想，我们可以得到：
$$(x_1\cdot x_2+1{)}^2=2{\alpha }_1{\eta }_1+2{\alpha }_2{\eta }_2+{\alpha }_1^2{\eta }_1^2+{\alpha }_2^2{\eta }_2^2+2{\alpha }_1{\alpha }_2{\eta }_1{\eta }_2+1$$

	可以直观的发现，式子的主要区别在系数上
	也就是说：
		只需要乘上一个系数，就可以将五维空间的内积转换成两维空间的内积
1
2
3

下面，我们再用实际数据来具体说明核函数的作用：

假设向量$x_1=(3,5)$，二阶扩展后得到：3,5,9,25,15
        $x_2=(4,2)$，二阶扩展后得到：4,2,16,4,8

进行二阶扩展时，我们会得到：
$$\varphi (x_1)\cdot \varphi (x_2)=3\ast 4+5\ast 2+9\ast 16+25\ast 4+15\ast 8=386$$
$$(x_1\cdot x_2+1{)}^2=(3\ast 4+5\ast 2+1{)}^2=529$$
$$[0.8476(x_1\cdot x_2)+1{]}^2=[0.8476(3\ast 4+5\ast 2)+1{]}^2=386.01$$

1. 核函数的分类

这里我们明确下SVM使用时，需要包含核函数和松弛因子

1.1 线性核函数(Linear Kernel)

	该核函数针对线性可分数据
		即：不需要做扩展，只点乘，其他什么都没做
1
2

$$K(x,z)=x\bullet z$$

1.2 多项式核函数(Polynomial Kernel)

	γ、r、degree扩展阶数 属于超参，需要调参
1

$$K(x,z)=(\gamma x\bullet z+r{)}^d$$

1.3 高斯核函数(Radial Basis Function Kernel)

	径向基函数核
	γ属于超参，要求大于0，需要调参
		常用核函数
1
2
3

$$K(x,z)=e^{-\gamma {\Vert x-z\Vert }^2}$$

1.4 Sigmoid核函数(Sigmoid Kernel)

	γ、r属于超参，需要调参
1

$$K(x,z)=\tanh (\gamma x\bullet z+r)$$

2. 核函数小节

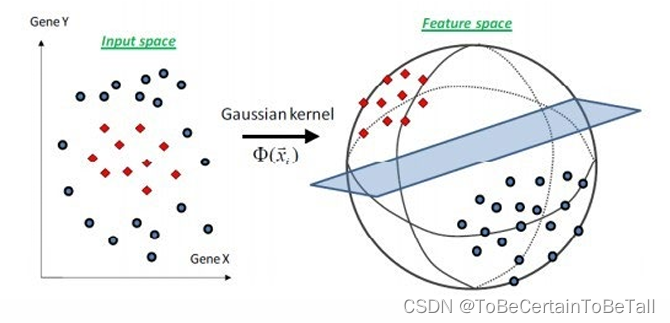
虽然核函数计算输出的结果与二阶扩展的结果一致，但核函数的价值在于，通过在低维上进行计算，从而达到高维上的分类效果，避免了直接在高维空间中的复杂计算

	核函数的作用：将非线性可分的数据转换为线性可分数据
	
	核函数可以自定义
		核函数必须是正定核函数，任何半正定的函数都可以作为核函数
			Gram矩阵是半正定矩阵：			
1
2
3
4
5