最短路算法笔记

2019年6月20日最短路算法讲义

算法大纲

Q群是Acwing算法交流群2:728297306.
因为四大最短路算法大家应该都明白,所以我们就不讲了,然后根据群友们提出的建议,我们今天讲一讲SPFA求负环,以及最短路和其他算法的配合,等方面的知识.

---

SPFA求负环

我们先来具体分析一下SPFA算法.

对于SPFA而言,我们发现它是具有几点特殊性质的.

第一步,从SPFA的核心点来分析.

$$(x,y,z)表示为(x,y)这条有向边的权值为z \\ dist[x]表示从1号节点到x号节点的最短路径$$
如果说我们发现图中出现如下这张图,那么我们就称之为三角不等式.

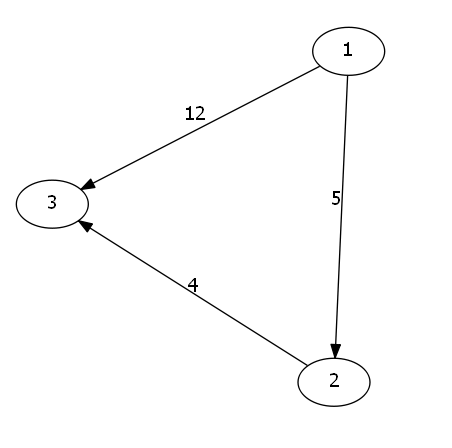
我们现在要从$1$号节点走到$3$号节点,然后我们发现了有这个不等式出现,那么就是三角不等式.

刚开始的话,我们的

$$dist[3]=dist[1]+ver[1][3]$$
但是当我们的$2$号节点出现后,就不一样了.
$$dist[3] \ge dist[2]+ver[2][3]$$
然后我们就不等不更新我们的$dist[3]$.所以就会出现如下操作
$$dist[3]=dist[2]+ver[2][3]$$
然后此时的话,我们就会发现,目前的$dist[3]$是满足三角不等式了.

综上所述三角不等式就是说

$$对于每一个点x而言,都必须满足dist[x] \le dist[y]+z,也就是说三角形的第三边,一定小于其他两边之和.$$
然后对于每一次不满足三角不等式的情况,也即是上图这种情况,我们都不得不更新$dist[3]$的值.

因此最短路上每一个节点,都得满足我们的三角不等式,否则的话,我们总可以,走一遍上图1->2->3来更新我们的最短路.

---

上面是我们的三角不等式解说,那么现在我们的核心问题点是如何求负环.

我们发现,如果说一张图上出现了负环,那么我们一定无法满足三角不等式.

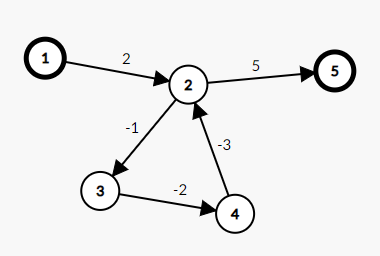
我们发现如果图中出现了负环,那么肯定我们的如果来到一个负环上的点,那么肯定是要经过这个负环所有的节点的.

什么是环?环就是这个点往其他点走了若干个节点后,还可以回到这个节点.

既然这么说的话,我们每走一次负环就可以让我们的权值减少一部分,那么既然如此的话,我们既然要走最短路,那么为什么不一直沿着这条最短路走呢?

所以说我们一定会不停地沿着这个负环走一遍又一遍,三角形不等式性质根本就无法满足,既然如此的话,我们就可以通过这个办法去找到负环.

我们知道下面这个性质.

$$从1号节点走到n号节点,那么途中肯定最多只会途经n个节点,n-1条边$$
既然有了这个性质,再加上如果有负环的话,那么我们会不停地经过负环上的每一条边,那么我们为什么不可以开一个数组记录一下呢.
$$设cnt[i]表示从1号节点到i号节点,途径cnt[i]条边.那么显然cnt[i] \ge n的话,就会出现负环$$
因此只有出现负环才会不停地访问负环上的边,普通的环是不会不停地访问的.

不过其实,我们还有一种判断方法.

如果我们发现

$$一个点入队次数超过了n,那么肯定也是负环出现了.$$
这是什么意思呢?

和上面的意思其实一样,假如说没有负环,那么一个点肯定不会被访问n次,毕竟

---

题目选讲

第一题

NOIP2017 Day1 T3

题目描述

策策同学特别喜欢逛公园。公园可以看成一张$N$个点$M$条边构成的有向图，且没有 自环和重边。其中1号点是公园的入口，$N$号点是公园的出口，每条边有一个非负权值， 代表策策经过这条边所要花的时间。

策策每天都会去逛公园，他总是从1号点进去，从$N$号点出来。

策策喜欢新鲜的事物，它不希望有两天逛公园的路线完全一样，同时策策还是一个 特别热爱学习的好孩子，它不希望每天在逛公园这件事上花费太多的时间。如果1号点 到$N$号点的最短路长为$d$，那么策策只会喜欢长度不超过$d + K$的路线。

策策同学想知道总共有多少条满足条件的路线，你能帮帮它吗？

为避免输出过大，答案对$P$取模。

如果有无穷多条合法的路线，请输出$-1$。

输入输出格式

输入格式：

第一行包含一个整数 $T$, 代表数据组数。

接下来$T$组数据，对于每组数据： 第一行包含四个整数 $N,M,K,P$，每两个整数之间用一个空格隔开。

接下来$M$行，每行三个整数$a_i,b_i,c_i$，代表编号为$a_i,b_i$的点之间有一条权值为 $c_i$的有向边，每两个整数之间用一个空格隔开。

输出格式：

输出文件包含 $T$ 行，每行一个整数代表答案。

输入输出样例

输入样例#1：

2
5 7 2 10
1 2 1
2 4 0
4 5 2
2 3 2
3 4 1
3 5 2
1 5 3
2 2 0 10
1 2 0
2 1 0

输出样例#1：

3
-1

说明

样例解释1

对于第一组数据，最短路为 $3$。 $1 – 5, 1 – 2 – 4 – 5, 1 – 2 – 3 – 5$ 为 $3$ 条合法路径。

测试数据与约定

对于不同的测试点，我们约定各种参数的规模不会超过如下

测试点编号	$T$	$N$	$M$	$K$	是否有0边
1	5	5	10	0	否
2	5	1000	2000	0	否
3	5	1000	2000	50	否
4	5	1000	2000	50	否
5	5	1000	2000	50	否
6	5	1000	2000	50	是
7	5	100000	200000	0	否
8	3	100000	200000	50	否
9	3	100000	200000	50	是
10	3	100000	200000	50	是

对于 100%的数据, $1 \le P \le 10^9,1 \le a_i,b_i \le N ,0 \le c_i \le 1000$。

数据保证：至少存在一条合法的路线。

---

解题报告

题意理解

这道题目题意就是让你,统计一下长度为$[d,d+k]$这个区间内从$1->n$的路径总数.

30pts

暴力统计

我们发现这道题目有三个点,也即是数据点1,2,7这三个点都是只需要我们找最短路的路径个数.

既然如此的话,我们不妨在最短路算法中,再开一个额外的数组统计路径个数,去拿到这三十分.

1.如果发现松弛操作的两种路径相等,也就是a->c=a->b+b->c，那么我们就将搜索到的点的路径数加上当前点的路径数，即：

    if(dis[i]==dis[k]+ver[k][i])
        cnt[i]+=cnt[k];

2.如果我们更新了搜索到的点到起点的最短距离,也就是a->c < a->b+b->c ，那么我们将到达改点的路径数改为当前点的路径数，也就是

    if(dis[i]>dis[k]+ver[k][i]){
        dis[i]=dis[k]+ver[k][i];
        cnt[i]=cnt[k];
    }

---

70pts

暴力思想

我们其实可以惊奇地发现,就是我们的$k \le 50$,这说明什么就是我们完全可以暴力地去统计,长度为$d,d+1,d+2,d+3,...,d+K$的所有路径.

综上所述我们可以通过搜索算法,去一步步暴力地搜索,找到符合条件的路径.

但是我们发现这个搜索显然复杂度太高了.

各大剪枝

我们对于当前这一步而言,如果说它花费了$w$点代价,然后接下来我们统统都以最优秀的最短路走到终点,花费$s$点费用.

然后我们惊奇地发现$w+s>d+k$,那么显然这一步是不合法的,因为它的最小花费代价都大于了我们的最大上限路径长度.

综上所述,第一个剪枝,就是我们的可行性剪枝.

但是我们如何统计一个点到终点的距离呢?难道我们要每一次都跑一遍最短路算法统计吗

其实我们可以通过建立一个反向图,来达到目的地.

1. 什么是反向图?

我们以样例为例子.

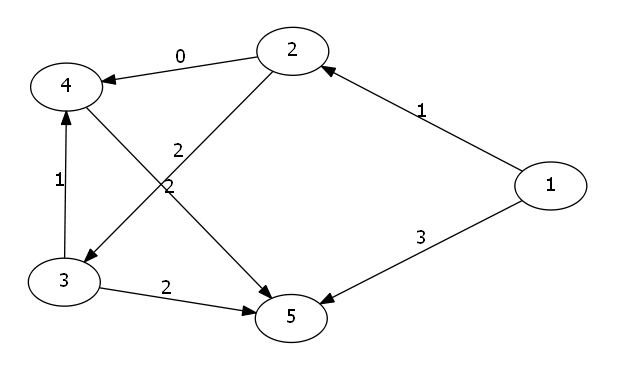
这张图叫做原图.

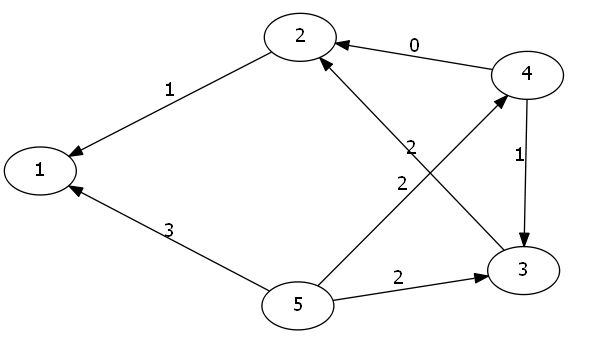
这张图就是我们的反向图.

所谓的反向图就是将方向统统反过来,原来是a->b,现在改成b->a

1. 反向图有什么用处

我们发现反向图最大的用处,就是统计一个点到终点的距离.

因为此时我们的起点是原来的终点N,而现在的终点变成了原来的起点1.所以我们最短路过后,每一个$dis[i]$表示为节点$N$到$i$的距离.

综上所述,我们就这么巧妙地处理了第一个可行性剪枝.

---

但是我们现在依旧发现了一个问题,我们的时间复杂度还是太高了,所以我们不得不进行记忆化剪枝,也就是利用了了动态规划的思想.

首先我们观察一下,路径长度为$d+1,d+2,d+3,d+4,...,d+K$的路径,他们具有以下特征.

1. 对于长度为$d+1$的路径而言,我们可以认为它是最短路情况下,多走了一点冤枉路.

2. 对于长度为$d+2$的路径而言,我们可以认为它是最短路情况下,多走了二点冤枉路.

3. 对于长度为$d+3$的路径而言,我们可以认为它是最短路情况下,多走了三点冤枉路.

将以上路径转化后,我们发现完全可以通过动态规划的思想去处理本问题.

我们设$f[i][j]$表示为,当前到达了点$i$,已经多走了冤枉路$j$.

那么我们发现状态转移方程也迎刃而解了.

$$f[u][w]=∑f[v][w+dis[u]−(dis[v]+ver[u][v])] \\ 0 \le w \le K \\ (u,v)为一条边 \\ ver[u][v]表示u到v的距离.\\ w表示当前走了w点冤枉路$$
我们解释一下上面的状态转移方程的核心点.
$$w+dis[u]-(dis[v]+ver[u][v]);$$
对于下面这个式子而言,它表示为从起点走到$v$所需要花费的最少长度.
$$dis[v]$$
那么我们的一条最短路径,且是从$u$走到$v$所花费长度为.
$$dis[v]+ver[u][v]$$
然后我们的从起点走到$u$所花费的最短长度显然为.
$$dis[u]$$
既然如此那么我们从起点走到$v**$的最短路径,减去,我们从起点走到$u$然后再走到$v$的最短路径,就是我们的多走冤枉路.**
$$dis[u]-(dis[v]+ver[u][v]);$$
综上所述,这就是我们的思路,那么最后的答案,显然就是.
$$Ans=\sum_{i=0}^{K}{f[n][i]}$$

---

100pts

经历了千辛万苦的你,发现如果按照楼上的思路写代码的话,你发现居然只有70pts.

那是因为你忽略掉了-1这种无解的情况.

而-1这个点,其实就是题目中出现了长度为0的一个环 简称0环.

如何判断呢?

1. 拓扑排序判断
2. Tarjan算法判断
3. 搜索的过程中,如果一个点两次进入我们的最短路,那么显然就是0环.

显然这道题目我们使用第三个算法判断.

---

代码解释

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;//数据范围
const int inf=1e9;//最大值
int t,n,m,k,p,ans,flag,vis[N],dis[N],dp[N][55],vis_dp[N][55],x,y,z;//变量
struct node//最近get到的结构体内置,好好玩啊.模板标记 
{
    int cnt,edge[N<<1],ver[N<<1],Next[N<<1],head[N];//记得边要乘以2,因为要建立反向图
    void init()//初始化
    {
        cnt=0;
        memset(head,0,sizeof(head));
    }
    void add_edge(int x,int y,int z)//建图
    {
        edge[++cnt]=y;
        ver[cnt]=z;
        Next[cnt]=head[x];
        head[x]=cnt;
    }
    void spfa(int s)//SPFA,NOIP是不会卡掉我们的.
    {
        int i,x;
        queue<int>q;
        for(i=1; i<=n; i++)
        {
            vis[i]=0;
            dis[i]=inf;
        }
        q.push(s),vis[s]=1,dis[s]=0;
        while(q.size())
        {
            x=q.front();
            q.pop();
            vis[x]=0;//出来了
            for(i=head[x]; i; i=Next[i])//遍历所有的出边
            {
                int y=edge[i],z=ver[i];
                if(dis[x]+z<dis[y])
                {
                    dis[y]=dis[x]+z;//更新
                    if(vis[y]==0)
                    {
                        q.push(y);
                        vis[y]=1;//标记
                    }
                }
            }
        }
    }
} g1,g2;
void clear()
{
    ans=0;
    flag=1;
    g1.init();//初始化很重要
    g2.init();
    memset(dp,-1,sizeof(dp));
}
int dfs(int x,int k)
{
    int i,j;
    if(~dp[x][k])//记忆化搜索
        return dp[x][k];
    vis_dp[x][k]=1;//标记进入了最短路径
    dp[x][k]=0;
    for(i=g2.head[x]; i; i=g2.Next[i])
    {
        int y=g2.edge[i],z=k+dis[x]-(dis[y]+g2.ver[i]);
        if(z>=0)//如果是在指定偏差区间内的
        {
            if(vis_dp[y][z])//之前已经进入过最短路径了,那么显然是无解了.
                flag=0;
            dp[x][k]+=dfs(y,z);//统计
            dp[x][k]%=p;//取得取模
        }
    }
    vis_dp[x][k]=0;//已经从最短路径中出来了.
    return dp[x][k];//该返回了
}
int main()
{
    scanf("%d",&t);
    while(t--)
    {
        clear();
        scanf("%d%d%d%d",&n,&m,&k,&p);
        for(int i=1; i<=m; i++)
        {
            scanf("%d%d%d",&x,&y,&z);
            g1.add_edge(x,y,z);
            g2.add_edge(y,x,z);//不是无向边,是建立反向图
        }
        g1.spfa(1);
        dp[1][0]=1;
        for(int i=0; i<=k; i++)
        {
            ans+=dfs(n,i);//每一个有冤枉路的路径都要加入
            ans%=p;//取模快乐 
        }
        dfs(n,k+1);//再来一下判断,主要是判断无解.因为长度为0~k时候走的路,如果和长度为k+1走的路一样,那么显然是无解
        if(!flag)//无解了
            puts("-1");
        else
            printf("%lld\n",ans);
    }
    return 0;
}