Matlab 机器人工具箱 (一）DH参数和正逆运动学_matlab 机器人工具箱 运动学

作者为大三学生，本博客为边学习边使用，如有错误，请见谅。

在文章结束附加代码。

一、DH参数

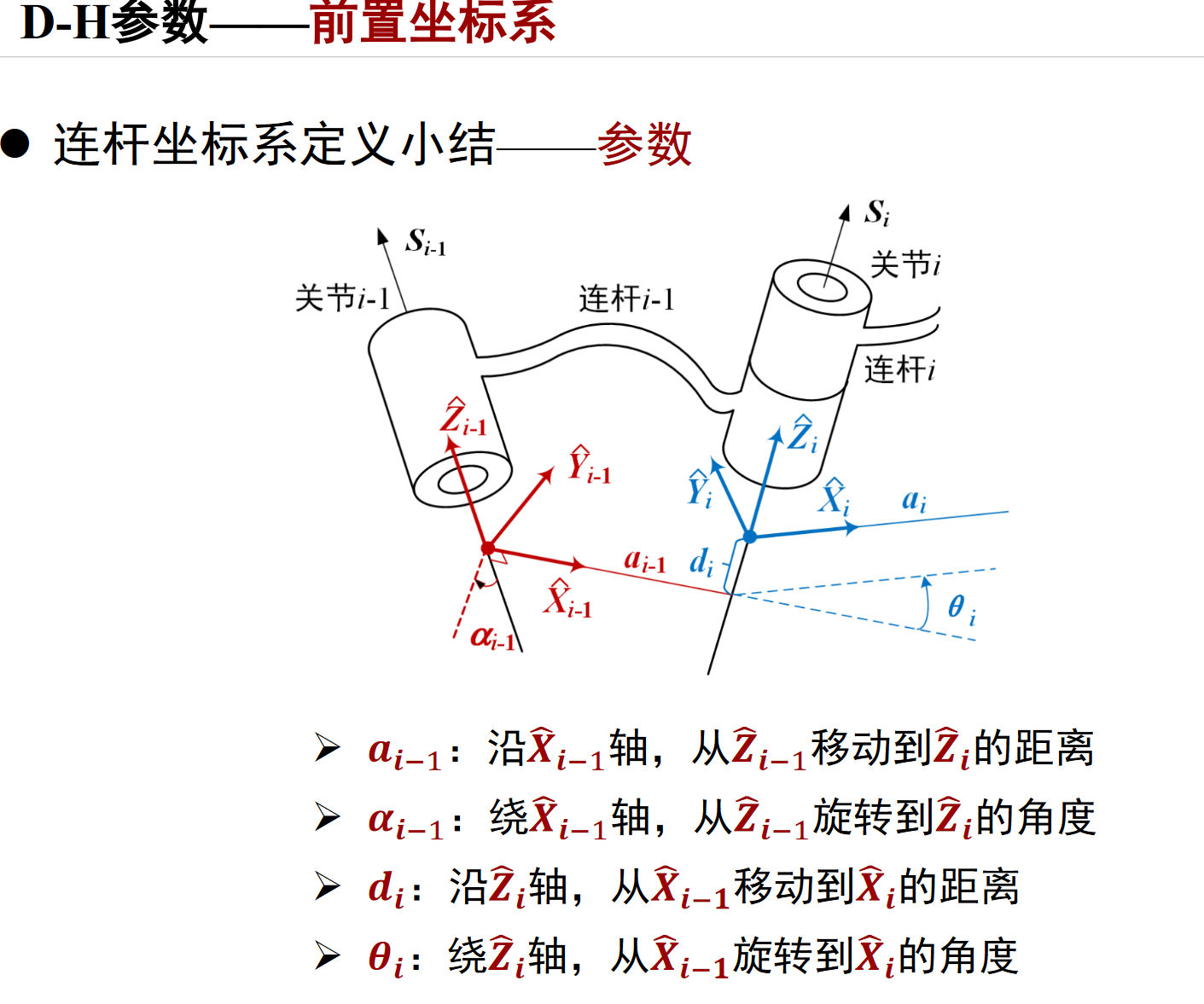
前置坐标系对应改进版：modified

后置坐标系对应标准版：standard

因为学习过程中大部分为前置坐标系，故本文仅讨论前置坐标系。

二、Link函数

用的最习惯的是如下的代码：

 L =Link([theta  D A alpha sigma offset], CONVENTION)

参数‘alpha’代表扭转角 ，参数‘A’代表杆件长度，参数‘theta’代表关节角，参数‘D’代表横距，参数‘sigma’代表关节类型：0代表旋转关节，非0代表移动关节。

参数CONVENTION可以取‘standard’和‘modified’，其中‘standard’代表采用标准的D-H参数，‘modified’代表采用改进的D-H参数。

一般是四个参数起步，如果输入的不到六个参数，则依次取前几项。

移动关节的移动轴为Z轴，在变换的时候记得特别注意。

操作函数

%  A               连杆变换矩阵
%  RP            关节类型: 'R' 或 'P'
%  friction      摩擦力
%  nofriction    摩擦力忽略

%  dyn           显示动力学参数
%  islimit       测试关节是否超出软限制
%  isrevolute    测试是否为旋转关节
%  isprismatic   测试是否为移动关节
%  display       连杆参数以表格形式显示
%  char          转为字符串

例如：

三、SerialLink函数

L(1) = Link([theta1, D1, A1, alpha1, sigma1,offset1], 'modified');
L(2) = Link([theta2, D2, A2, alpha2, sigma2,offset2], 'modified');
L(3) = Link([theta3, D3, A3, alpha3, sigma3,offset3], 'modified');
L(4) = Link([theta4, D4, A4, alpha4, sigma4,offset4], 'modified');
robot = SerialLink(L,'name','four');

这个创建还是比较简单的。

操作函数

%  plot          以图形形式显示机器人

%  teach         驱动机器人

%  isspherical   测试机器人是否有球腕关节

%  islimit       测试机器人是否抵达关节极限

%  fkine         前向运动学求解

%  ikine6s       6旋转轴球腕关节机器人的逆向运动学求解

%  ikine3        3旋转轴机器人的逆向运动学求解

%  ikine         采用迭代方法的逆向运动学求解

%  jacob0        在世界坐标系描述的雅克比矩阵

%  jacobn        在工具坐标系描述的雅克比矩阵

%  maniplty      可操纵性度

%  jtraj         关节空间轨迹

%  accel         关节加速度

%  coriolis      关节柯氏力

%  dyn           显示连杆的动力学属性

%  fdyn          关节运动

%  friction      摩擦力

%  gravload      关节重力

%  inertia       关节惯性矩阵

%  nofriction    设置摩擦力为0

%  rne           关节的力/力矩

%  payload       在末端坐标系增加负载

%  perturb       随机扰动连杆的动力学参数

例如：

robot.plot([0 0 0 0]);
robot.teach();

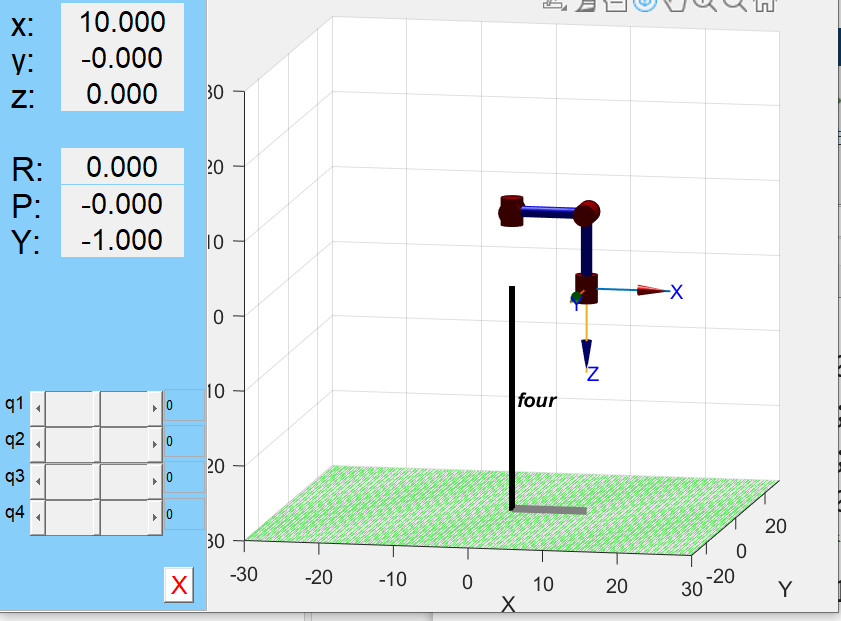
（紧跟着上面的代码）

正解 fkine

在输入未知参数的时候，会出现数据溢出的情况，于是我去查了fkine的源码

如下是源码的解析

这个函数用于计算给定关节配置下机器人末端执行器的位姿。以下是函数的一些关键部分解释：

• 在输入参数中，robot 是一个 SerialLink 对象，q 是关节坐标。如果 q 是矩阵，则会计算每个关节坐标对应的末端执行器位姿，并返回结果的三维矩阵。
• 如果 opt.deg 为真，则假设关节坐标是角度而不是弧度（默认为假）。
• 如果需要输出所有关节坐标对应的各个关节坐标系的位姿，可以通过设置 nargout 大于 1 来实现。
• L 是机器人的关节链信息。
• 如果 q 是一个列向量（关节坐标），则会依次计算每个关节坐标对应的变换矩阵，并将其与之前的变换矩阵相乘。
• 如果 q 是一个矩阵（多个关节坐标），则会循环计算每个关节坐标对应的变换矩阵，并将结果存储在 t 中。

这个函数的作用是根据给定的关节坐标计算机器人末端执行器的位姿。它可以根据单个关节坐标或多个关节坐标计算。并且在识别接收到符号函数的时候，会将矩阵转换为符号矩阵进行运算。

也就是说，其实不应该出现数据溢出的情况。那这是为什么呢

其实是由于浮点数运算导致的。

如果一个浮点数矩阵与含符号变量的矩阵相乘，又恰好涉及到0的运算，就会出现数据溢出等情况。（根据实际操作得出结论，不知道具体原理，欢迎大佬在评论区探讨）

本周作业为一个四关节自由度的正运动学解算，用符号参数表示最终结果。我写了如下代码。

syms s1 s2 s3 s4 l0 l2 d4 real;
theta(1) = 0; D(1) = 0;  A(1) = 0;  alpha(1) = 0;     sigma(1)=0; offset(1) = 0;
theta(2) = 0; D(2) = 0;  A(2) = 0;  alpha(2) = pi/2;  sigma(2)=0; offset(2) = 0;
theta(3) = 0; D(3) = 0;  A(3) = 1;  alpha(3) = 0;     sigma(3)=0; offset(3) = 0;
theta(4) = 0; D(4) = 1; A(4) = 0;  alpha(4) = pi/2;  sigma(4)=1; offset(4) = 0;
%DH法建立模型,关节转角，关节距离，连杆长度，连杆转角，关节类型（0转动，(1)移动），'standard'：建立标准型D-H参数
L((1)) = Link([theta(1), D(1), A(1), alpha(1), sigma(1),offset(1)], 'modified');
L((2)) = Link([theta(2), D(2), A(2), alpha(2), sigma(2),offset(2)], 'modified');
L((3)) = Link([theta(3), D(3), A(3), alpha(3), sigma(3),offset(3)], 'modified');
L((4)) = Link([theta(4), D(4), A(4), alpha(4), sigma(4),offset(4)], 'modified');
robot = SerialLink(L,'name','four');
robot.plot([0 0 0 0],'workspace',[-10,10,-10,10,-10,10)];
robot.teach();
 
 

逆解ikine

     

该函数用于求解机器人的逆运动学问题，即根据机器人末端执行器的位置和姿态，计算出机器人关节角度值。主要介绍了函数的使用方式和参数及返回值的含义，其中包括：

1. 输入参数：

• T：表示末端执行器的位置和姿态，是一个4x4的齐次变换矩阵。
• Q0：表示初始估计的机器人关节角度值（可选参数，默认为0）。
• M：表示掩码矩阵，用于指定忽略的自由度（可选参数）。
• OPTIONS：表示优化选项（可选参数）。

1. 返回值：

• Q：表示计算得到的机器人关节角度值，是一个MxN的矩阵。

其中，M表示末端执行器位置和姿态的数量，N表示机器人的自由度数目。

此外，注释还介绍了一些注意事项，如：

• 该函数使用伪逆方法和迭代算法求解逆运动学问题。
• 逆运动学解不唯一，取决于初始估计值。
• 伪逆方法可以在奇异点处得到解，但是在零空间内的关节角度值是任意的。

另外，ikine函数无法接受一个含函数参量的T矩阵进行运算，这样会出现一些问题，会报错。

这就说明，用参数表示的时候只能手搓。

作业是求一个六自由度的机械臂的逆运算，还是用参数表示，出题人真的动脑子？

结束！