Transformer_transformer神经网络

edited by nrzheng，2021.11.25

---

参考视频

参考链接

transformer

1. 概述

1.1. 网络整体结构

transformer网络结构如下图所示：

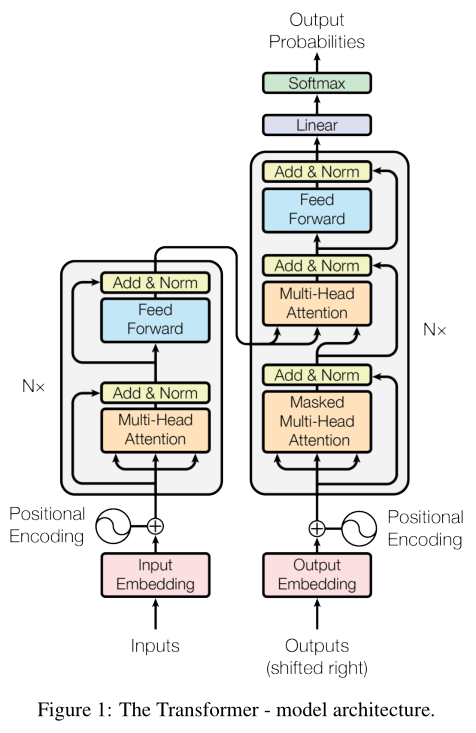
• 注意！！！！！！！！！！
• transformer的输入是有两个的，一个在Encoder， 一个在Decoder（机器翻译是这样）

1.2. 网络结构大致解析

从全局角度先看看，transformer在做一个什么事：

TRM一开始是在机器翻译中被提出的，整个过程可以概括为下图：

不用管里面怎么做，总之经过TRM这个黑盒的操作，“我爱你”就变成了“I LOVE YOU”。

然后我们细化TRM的操作，一步一步细化。

1. 输入没有发生变化，输出也没有发生变化，把TRM分成两个部分，Encoders和Decoders：

• 也就是说“我爱你”作为输入，经过Encoders，然后Encoders输出再作为Decoders的输入，流出来，就变成“I LOVE YOU”

2. Encoders和Decoders就是由n个Encoder和n个Decoder组成的：

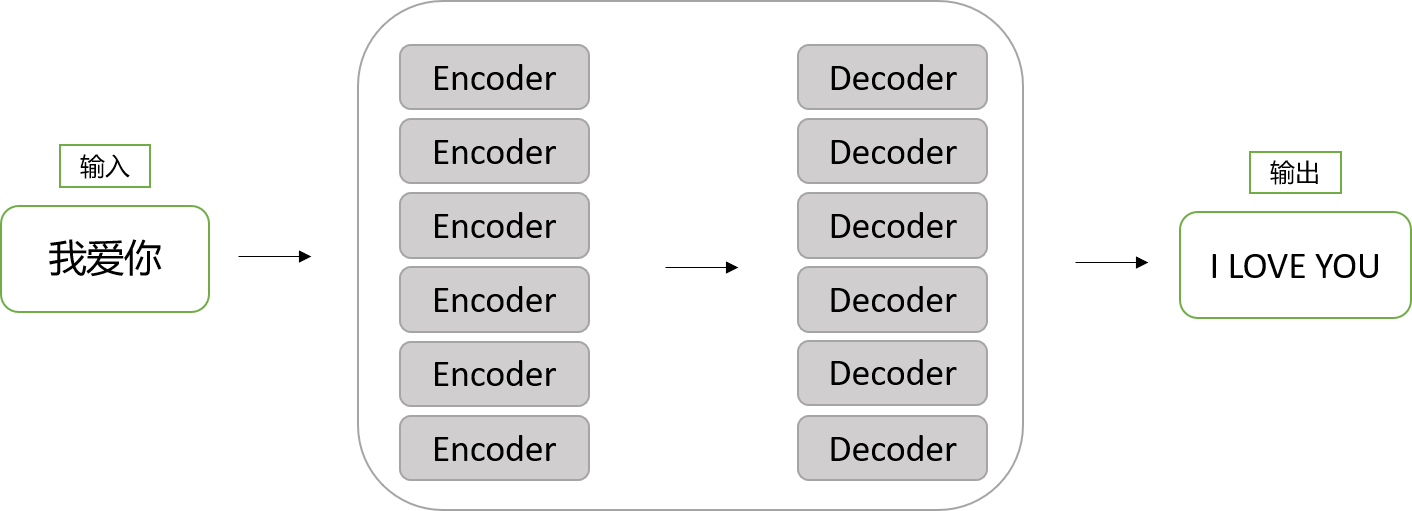
• 也就是流经多个Encoder和多个Decoder，就可以把“我爱你”变成“I LOVE YOU”
• 上图二者的个数都是6，这个数字可以自己定
• 需要注意的是，6个Encoder的结构是完全相同的，6个Decoder的结构也是完全相同的
• 但是，只是结构相同，参数是不一样的，都在训练
• Encoder和Decoder是不一样的
• 这个其实就是1.1中的那个网络结构图了，里面不是有*n嘛。（可以上去翻看看）
• （这里的每一小个Encoder就是1.1网络结构图的左半部分，每个Decoder就是右半部分）

3. 需要注意的是：

• Encoder和Decoder架构是不一样的
  • 多了一层交互层
  • Decoder中的多了一个“Masked”

2. Encoder

2.1. Encoder概况

Encoder可以划分为三部分，如下图所示：

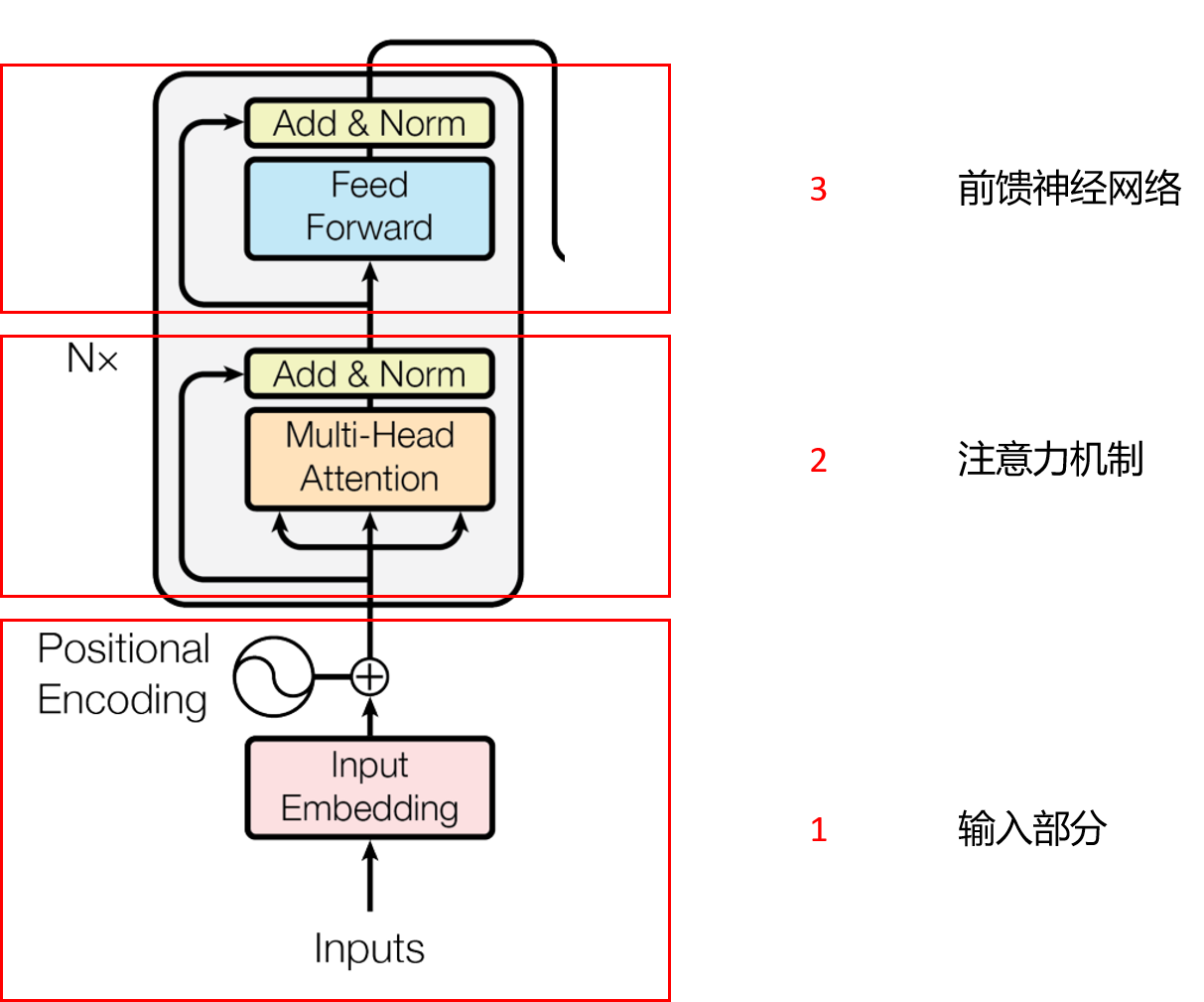
2.2. 输入部分

输入部分分为两个，一个是Embedding，一个是位置嵌入

2.2.1. Embedding

Embedding是NLP里面简单的入门知识

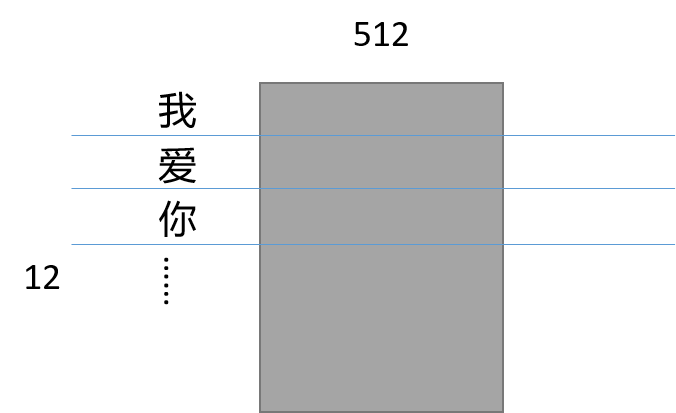
比如我们的输入句子是“我爱你…”，一共12个字，我们按字切分，每个字定义为一个512维度的字向量。这个字向量可以使用随机初始化或者word2vector

• 可以理解成图像中，用(255, 0, 0)代表红色，然后再用0代表(255, 0, 0)，然后再onehot，用000001之类的代表0
• 就是把一个字，用计算机能理解的语言代替

2.2.2. 位置嵌入 / 位置编码

1. 为什么需要位置编码？这里从RNN引出举例

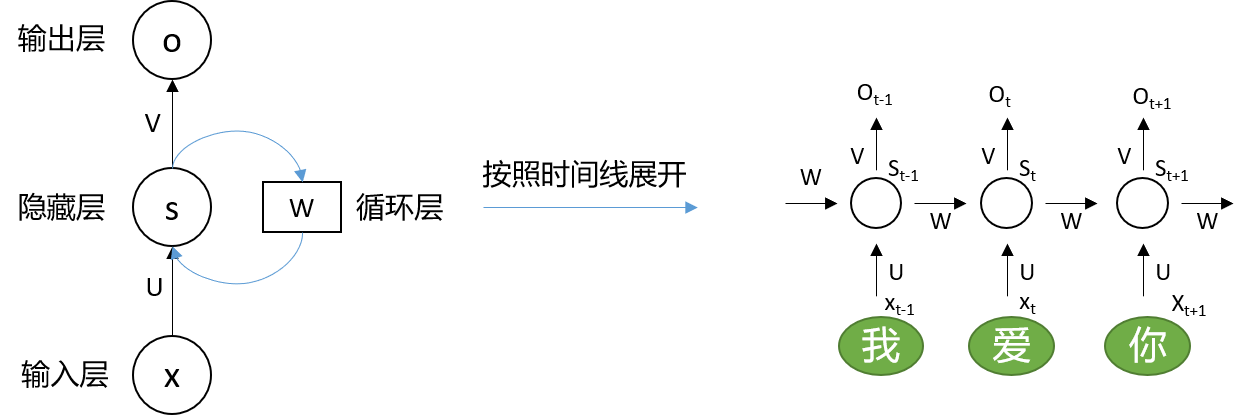
• U：RNN的输入参数，W：隐层参数，V：输出参数。对于RNN的所有time step都共享同一套参数。就是说，有100个词，都是用这么一套参数
• 按照时间线展开（上图右），可以看到其中的U，W，V都是一样的，没有上下标，就是一套参数
• （插）RNN的梯度消失是怎么来的？
  • 和普通网络的梯度消失含义不一样，它的梯度是总的梯度和
  • 它的梯度消失不是变为0，而是说总梯度被近距离梯度阻挡，被远距离梯度忽略不计

所以说RNN这种结构对于处理天然的时序关系的东西很符合。就是说先处理一个东西，再处理另一个东西。

但是对于transformer来说，它是有多头注意力的，也就是说，是一下子读了好多词进去。不是像RNN，输入一个“我”，等处理完，再处理“爱”。它是一起处理的

这样做增快了速度，但是忽略了单词之间的先后关系，所以说transformer想比于RNN就缺少了某种东西，告诉模型，某些单词是在前面还是后面

所以需要位置编码

2. 位置编码

位置编码的公式如下所示：
$$\begin{gathered} P{E}_{(pos,2i)}=sin(pos/10000^{2i/d_{model}}) \\ P{E}_{(pos,2i+1)}=cos(pos/10000^{2i/d_{model}})\text{\hspace{1em}(1)} \end{gathered}$$

• pos指的是position
• 2i就是偶数位，2i+1就是奇数位
• 在位置2i处，使用sin；在位置2i+1处，使用cos

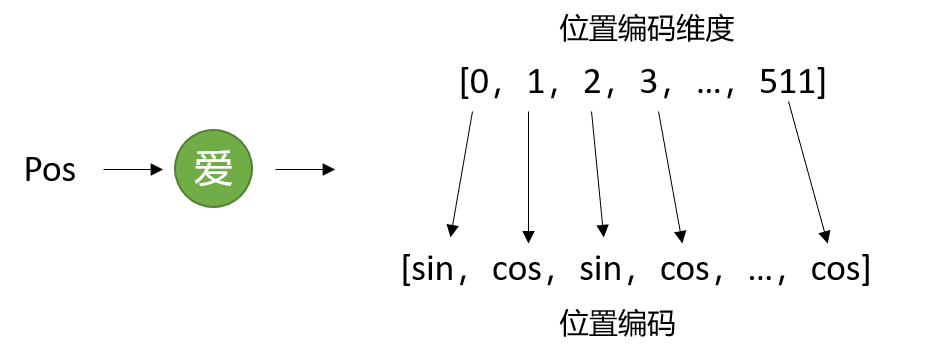
3. 得到位置编码之后，把位置编码和Embedding相加，得到一个512维的向量，作为整个transformer中Encoder的输入

4. 为什么位置编码会有用？

借助上述公式，我们可以得到一个特定位置的$d_{model}$维的位置向量，并且借助三角函数的性质：
{ s i n ( α + β ) = s i n α c o s β + c o s α s i n β c o s ( α + β ) = c o s α c o s β + s i n α s i n β (2)

$$\begin{cases} sin(\alpha+\beta)=sin\alpha cos\beta+cos\alpha sin\beta\\ cos(\alpha+\beta)=cos\alpha cos\beta+sin\alpha sin\beta \end{cases}$$ \tag{2} {sin(α+β)=sinαcosβ+cosαsinβcos(α+β)=cosαcosβ+sinαsinβ​(2)

我们可以得到：
{ P E ( p o s + k , 2 i ) = P E ( p o s , 2 i ) × P E ( k , 2 i + 1 ) + P E ( p o s , 2 i + 1 ) × P E ( k , 2 i ) P E ( p o s + k , 2 i + 1 ) = P E ( p o s , 2 i + 1 ) × P E ( k , 2 i + 1 ) − P E ( p o s , 2 i ) × P E ( k , 2 i ) (3)

$$\begin{cases} PE(pos+k,2i)=PE(pos,2i) \times PE(k,2i+1)+PE(pos,2i+1) \times PE(k,2i) \\ PE(pos+k,2i+1)=PE(pos,2i+1) \times PE(k,2i+1)-PE(pos,2i) \times PE(k,2i) \end{cases}$$ \tag{3} {PE(pos+k,2i)=PE(pos,2i)×PE(k,2i+1)+PE(pos,2i+1)×PE(k,2i)PE(pos+k,2i+1)=PE(pos,2i+1)×PE(k,2i+1)−PE(pos,2i)×PE(k,2i)​(3)
可以看出，对于$pos+k$位置的位置向量某一维$2i$或$2i+1$而言，可以表示为，$pos$位置与$k$位置的位置向量的$2i$与$2i+1$维的线性组合，这样的线性组合意味着位置向量（绝对位置）中蕴含了相对位置信息。但是这种相对位置信息会在注意力机制那里消失。

（正弦和余弦函数具有周期性，对于固定长度偏差k（类似于周期），post+k位置的PE可以表示成关于pos位置PE的一个线性变化（存在线性关系），这样可以方便模型学习词与词之间的一个相对位置关系）

2.3. 注意力机制

$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{k}})V\text{\hspace{1em}(4)}$$

2.3.1 注意力

（用一个婴儿在看一张报纸的图片举例，图片就不放了）

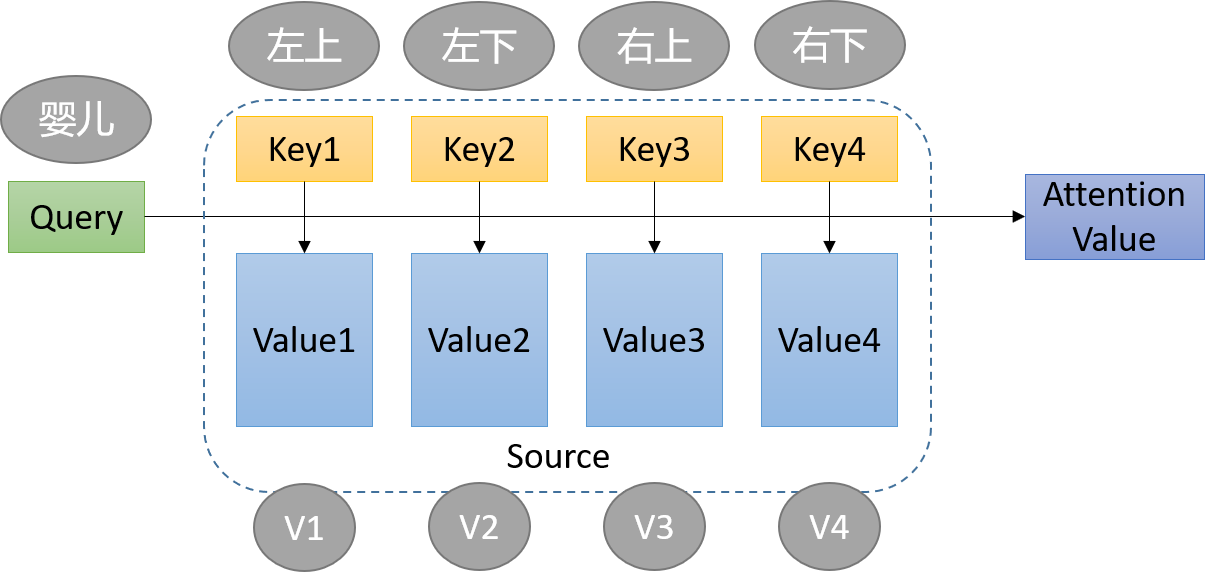
• 左上、左下、右上、右下、V1、V2、V3、V4、婴儿。都是拿来举例的，就是QKV，向量
• 婴儿分别个左上、左下、右上、右下，做点乘。得到的数值越大，说明距离越近，越相似，越关注，就是越相关呗。
• 然后再和V相乘，就相当于是加权。

（详见下图解析）

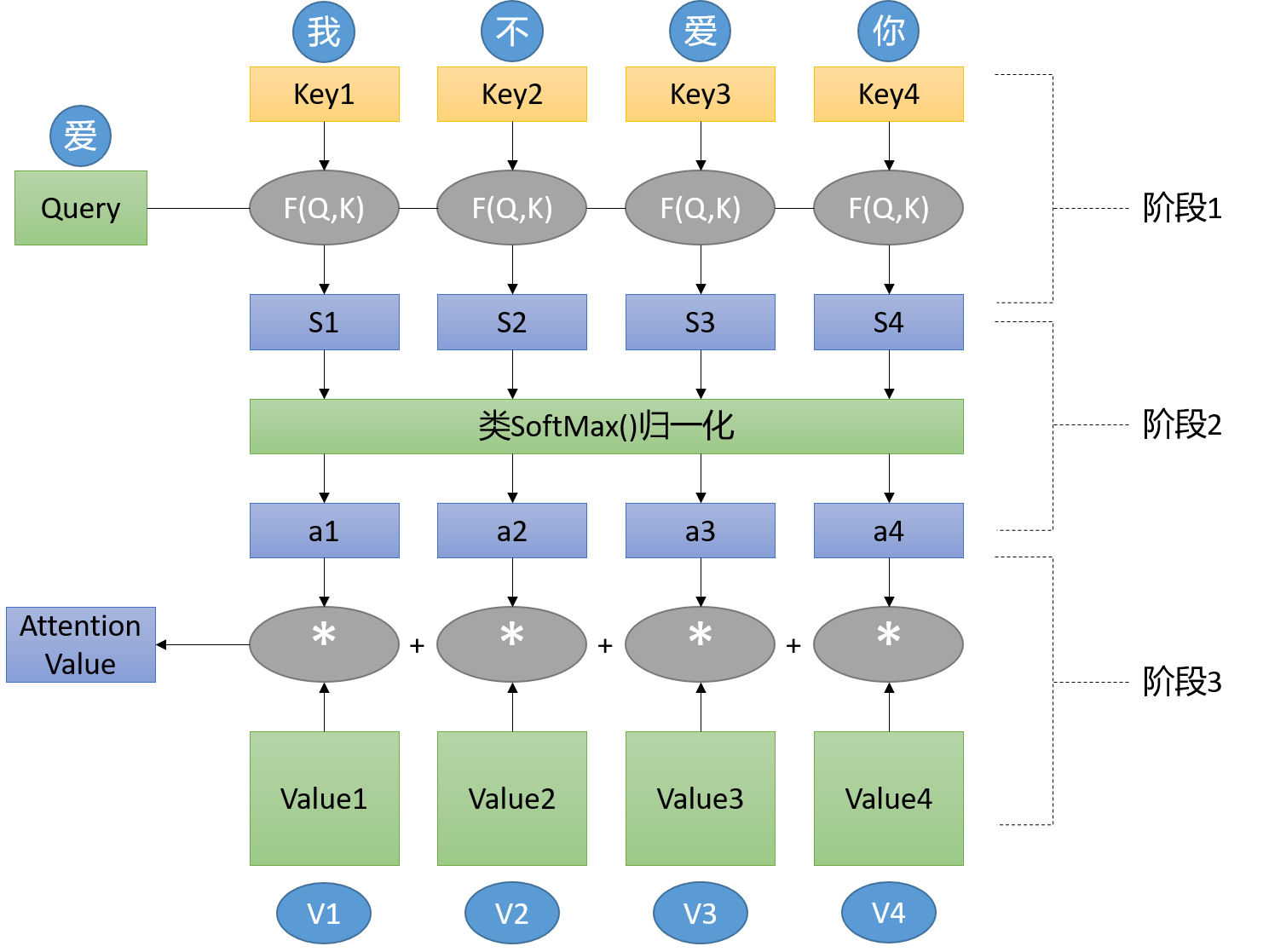
• 把Q和K1、K2、K3、K4做F函数变换。也就是“爱”和“我”，“不”，“爱”，“你”做F函数变换
• F函数变换可以有几种操作，一般用点乘
• 得到S1、S2、S3、S4结果，再做SoftMax得到a1、a2、a3、a4。这四个相加是等于一的（假设是[0.1, 0.1, 0.7, 0.1]）
• 然后和Value值相乘，再相加，就是加权。
• 除以$\sqrt{d_k}$是因为QK相乘的值很大，这样SoftMax之后，梯度就会很小（为什么很小，看看SoftMax函数就知道了）。除以$\sqrt{d_k}$而不是别的数，是为了控制方差为1
• 在实际操作用，使用矩阵，方便并行。

2.3.2 多头的操作

假设现在有一些句子X，X的维度是$[batchsize,sequencelength]$。

在2.2之后，我们有了transformer的输入，也就是Embedding和位置编码的和。可以得到$X_{embedding}\in [batchsize,sequencelength,embeddingdimension]$。为了学到多重含义的表达，对$X_{embedding}$做线性映射，也就是分配三个权重：
$$W_Q,W_K,W_V\in {\Re }^{embed.dim.\times embed.dim.}\text{\hspace{1em}(5)}$$
线性映射之后形成三个矩阵，为Q，K，V，和线性变化之前的维度一致，线性变换的公式：
$$\begin{gathered} Q=Linear(X_{embedding})=X_{embedding}{W}_Q \\ K=Linear(X_{embedding})=X_{embedding}{W}_K \\ V=Linear(X_{embedding})=X_{embedding}{W}_V\text{\hspace{1em}(6)} \end{gathered}$$
接下来就是多头注意力机制，（这几步的）流程图如下：

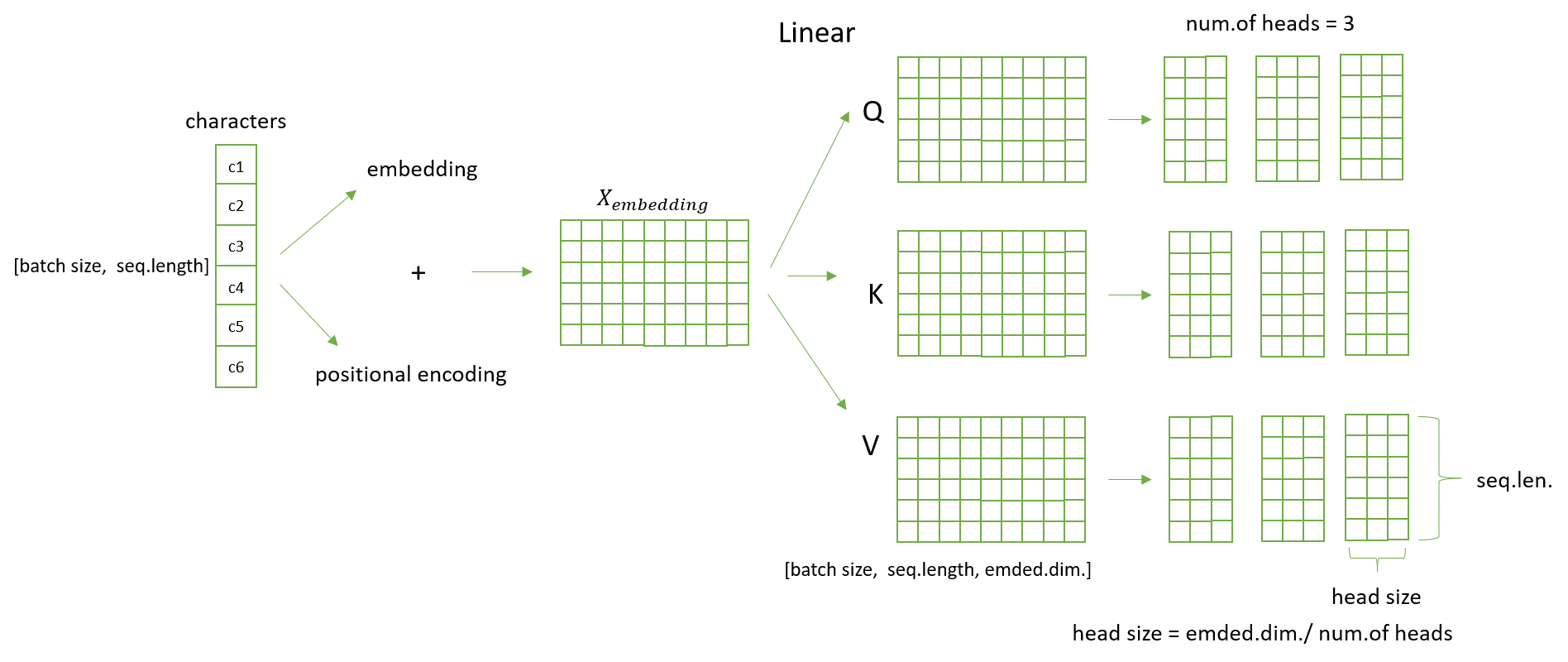
进行MHSA，我们要定义一个超参数h，也就是head的数量，注意，embedding dimension必须整除于h，因为要把它分成h份。

分割后：
$$Q,K,V\in [batchsize,sequencelength,h,embeddingdimension/h]$$
为了方便计算，进行转置，转置后：
$$Q,K,V\in [batchsize,h,sequencelength,embeddingdimension/h]$$

我们拿出一组来解释（QKV的计算）：

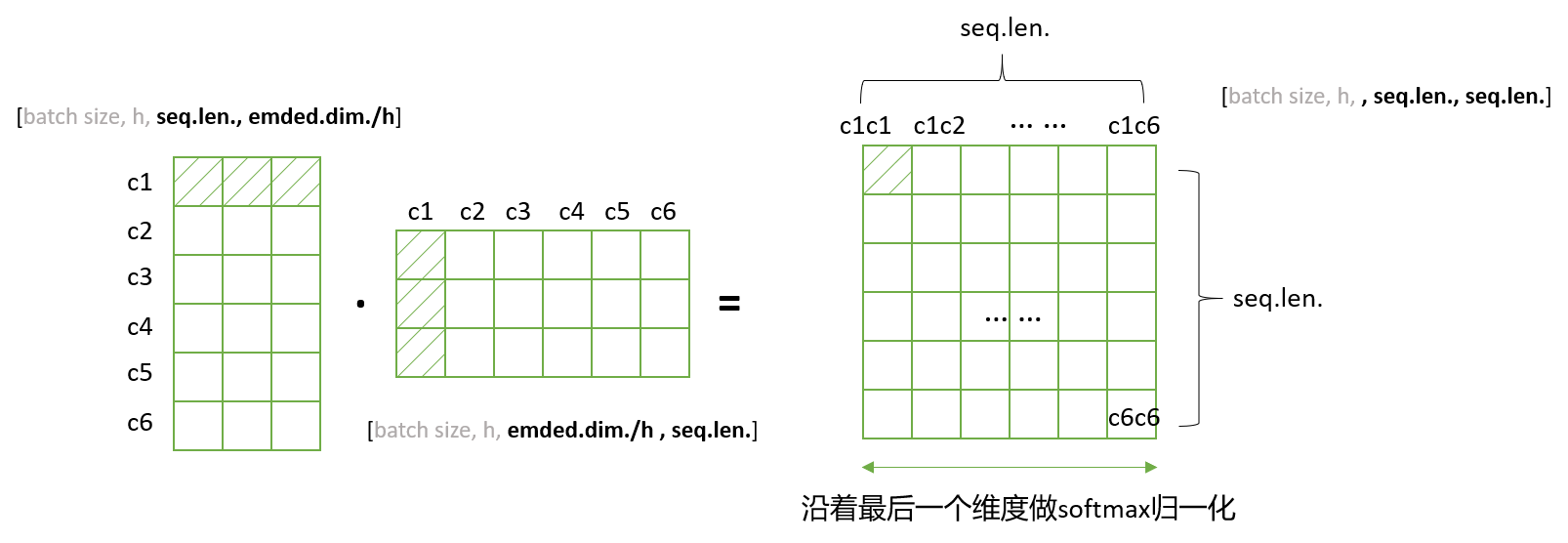
• 如上图所示，先计算Q与K的转置的点积。（点积的几何意义上面解释了）
• 点击的结果就是生成注意力矩阵。注意力矩阵的第一行就是第一个字c1与这六个字分别的相关程度。
• 然后用SoftMax进行归一化，这样每个字跟其他所有字的注意力权重的和为1
• 接着用注意力矩阵给V加权，见下图

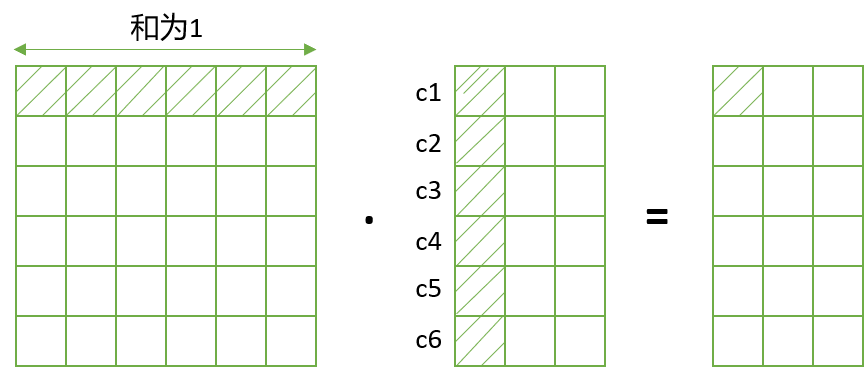
上图中我们从注意力矩阵中取出一行（和为1）然后依次点乘V的列，矩阵V的每一行代表着每个字向量的数学表达。上图的操作正是用注意力权重进行这些数学表达的加权线性组合，从而使每个字向量都含有当前句子内所有字向量的信息。

注意进行点积运算之后，V的维度没有变化哦。还是$[batchsize,h,sequencelength,embeddingdimension/h]$

在上面的self attention的计算过程中，我们通常采用mini batch来计算，也就是一次计算多句话，也就是$X\in [batchsize,sequencelength]$，sequence length 是句长。而一个mini batch是有多个不等长的句子组成的，我们就需要按照这个mini batch中最大的句长对剩余的句子进行补齐长度，一般使用0来填充，也就是padding。

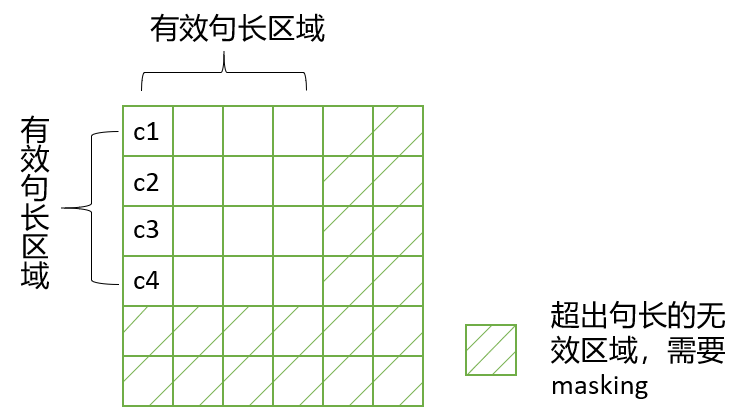
但是在这时进行SoftMax就会产生问题。SoftMax函数如下：
$$\sigma (z)=\frac{e^{z_i}}{{\sum }_{j=1}^k{e}^{z_j}}\text{\hspace{1em}(7)}$$
e的0次方是1，是有值的，这样的话softmax中被padding的部分就参与了运算，就等于是让无效的部分参与了运算，会产生很大的隐患，这时就需要做一个mask让这些无效区域不参与运算，我们一般给无效区域加一个很大的负数的偏置，也就是：
$$\begin{gathered} z_{illegal}=z_{illegal}+bia{s}_{illegal} \\ bia{s}_{illegal}\to -\infty \\ {e}^{z_{i}llegal}\to 0\text{\hspace{1em}(8)} \end{gathered}$$
经过上式的masking我们使无效区域经过softmax计算之后还几乎为0，这样就避免了无效区域参与计算。

2.4. 残差和LayerNorm

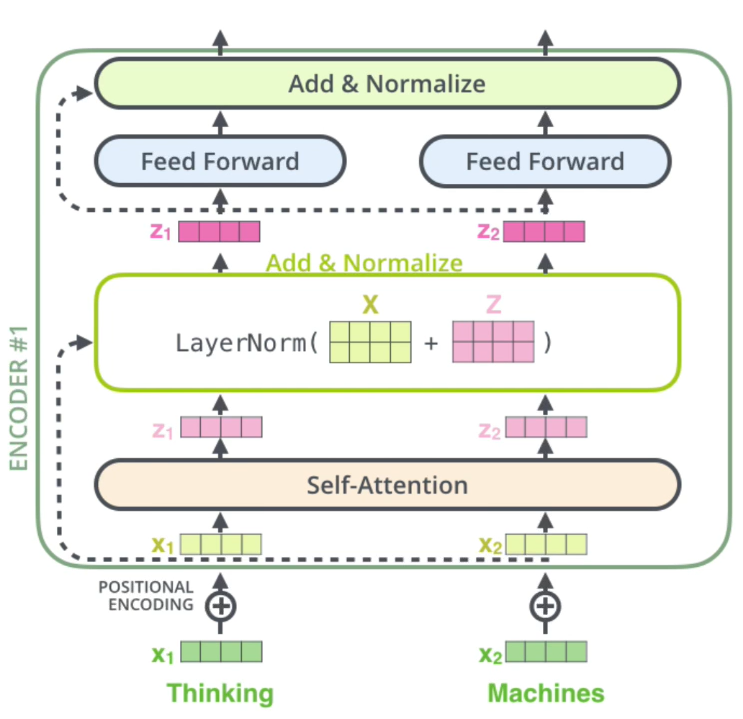
2.4.1. 残差

略了。可以去看ResNet的那篇笔记

上图就是把x拿过去跟z相加，再放进去LayerNorm

2.4.2. LayerNorm

为什么使用Layer Normalization，而不是使用常用的Batch Normalization？

• 因为BN效果差，所以不用

为什么BN效果差呢？

• BN是针对整个Batch中的样本，在同一维度的特征做处理
• LN则不一样，具体见下图

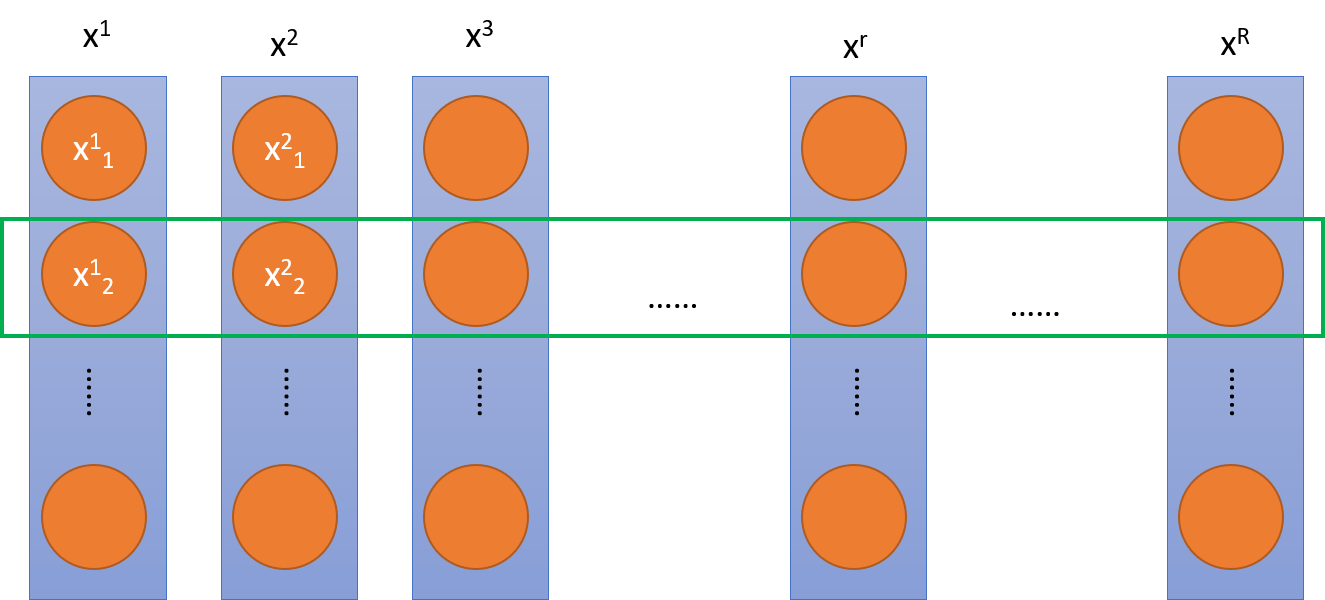
• 这边用班级同学的例子来解释
• 每一列代表不同的样本，也就是同学（小明、小红、…）
• 每一行代表一个特征，也就是（体重、身高、成绩、…）
• BN是针对所有样本的每一个特征做BN，比如：体重做BN、身高做BN、成绩做BN（也就是上图绿色框框）
• （LN是对一个样本的所有特征做归一化，就是上图的一列。下面会具体解释为什么这样好）
• BN的优点：
  • 解决内部协变量偏移（什么隐藏层啥的，不懂，不用深究）
  • 缓解梯度饱和问题（如果使用sigmoid激活函数的话），加快收敛
• BN的缺点：
  • batch size较小的时候，效果差
    • 很容易理解，因为BN就是用batch的均值和方差来模拟所有样本的均值和方差。batch size小了误差就大了
    • 如小明一个人的均值和方差，就不能代表全班的
  • BN在RNN中效果比较差，这一点和第一点原因很类似
• 可以看到，在这个例子中，BN很合理，因为对所有人的身高、体重等做BN，很合理
• 但是，用在NLP中，就会有很大的问题

为什么使用LayerNorm？为什么LayerNorm单独对一个样本的所有单词做缩放可以起到效果。

• 接下来用NLP来举例
• 上图每一列当作一个句子。比如：第一列是我爱中国共产党；第二列是今天天气真不错
• 可见，如果用BN的话，就是“我”和“今”做均值方差，“爱”和“天”做均值方差，…。它代表的意思就是“我”和“今”代表同样的语义信息…
• LN针对的就是“我爱中国共产党”来做均值和方差。它默认的意思就是“我爱中国共产党”在同一个语义信息里面
• （这是视频作者自己的理解）

2.5. 前馈神经网络

（就是两层的全连接）没啥好说的

• 用了两层全连接层，激活函数都是ReLU，可以看成是两层1*1的1维卷积
• 尺度变化为512—2048—512
• 公式如下：

$$FFN(x)=max(0,x{W}_1+b_1)W_2+b_2$$

3. Decoder

3.1. Decoder概况

Decoder可以划分为两部分，如下所示：

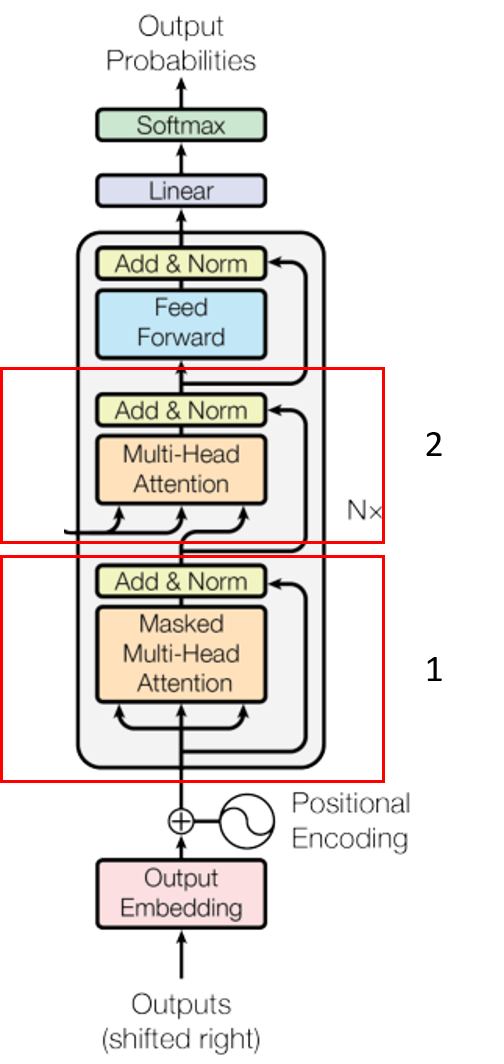
3.2. Decoder中的多头注意力机制

注意，Decoder中的多头注意力机制多了一个Masked，为什么要masked呢？

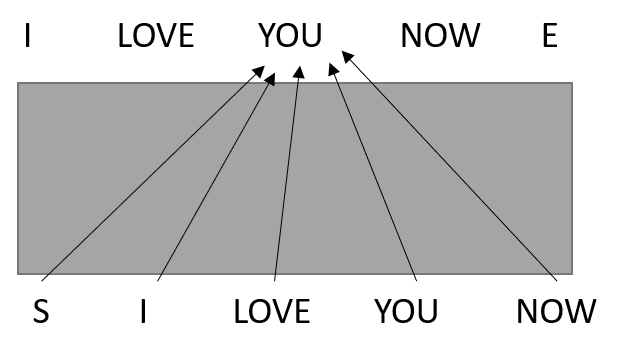
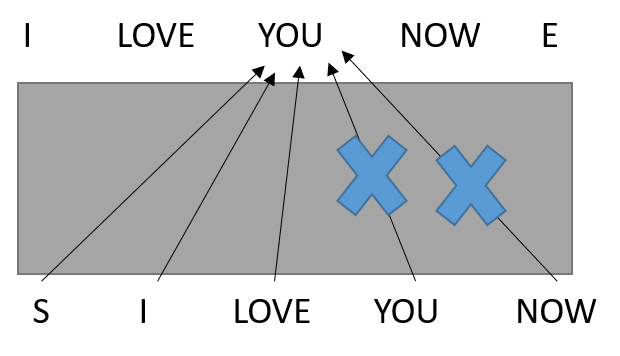
• Masked操作就是把当前词及其之后的全部都不看！！！
• 假设在输入“LOVE”的时候，Decoder没有masked，和Encoder的多头注意力机制一样结构的话
• 那么，“S”、“I”、“LOVE”、“YOU”、“NOW”就都会为“YOU”的预测输出提供信息
• 但是，这样训练出来的模型，在训练阶段会出现问题
• 因为预测的时候。是没有真值的，也就是说，后面的句子是看不到的。那么预测就会有问题。
• 所以说，在训练的时候，Decoder中的多头需要Masked掉
• 训练跟预测保持了一致性
• （记住，transformer的输入是有两个的，一个在Encoder，一个在Decoder，中间还有一个交互）

3.3. Dncoder和Decoder的交互层

Encoder生成KV矩阵，Decoder生成Q矩阵，然后进行普通的多头注意力机制

4. 代码

4.1. 三类应用

1. Encoder和Decoder共同使用：机器翻译类应用
2. 只使用Encoder：文本分类BERT和图片分类VIT
3. 只使用Decoder：生成类模型

4.2. 代码详解

sentences = ['ich mochte ein bier P', 'S i want a beer', 'i want a beer E']
1

• 里面有三个句子，但是我们要明白，这算是一组句子。也就是说属于一个样本，batch size等于1的

  • 如果batch size要等于4，那就是有4组句子，如果都是上面那个的话，那就是4组句子，每组句子里面有三个句子

• 有两个问题：

  • 这三个句子分别代表什么，怎么被模型处理掉
  • 三个句子中的特殊符号，P、S、E，分别代表什么

• 第一个问题：

  1. 看一眼transformer网络结构图，我们要明白，它是有两个输入的，一个是编码端的输入，一个是解码端的输入

  2. 抽离出来，放到机器翻译中来看：

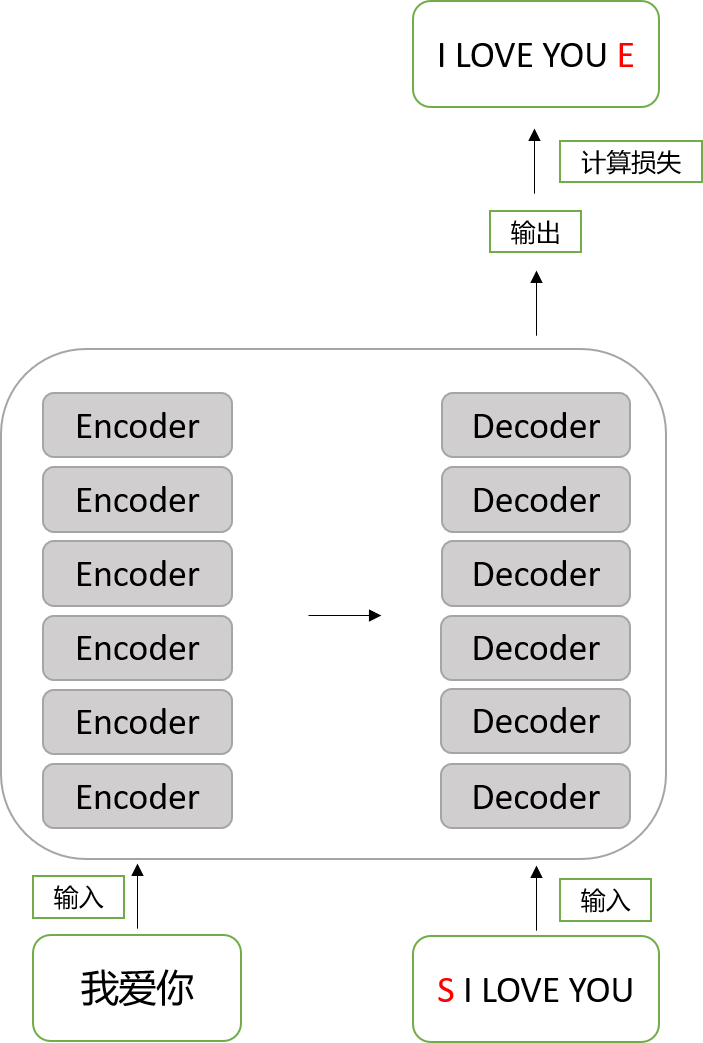
3. “我爱你”是编码端的输入，“S I LOUE YOU”是解码端的输入

4. “I LOVE YOU E”不是解码端的输出，这是解码端的真实标签

5. 解码端输出会跟真实标签做损失

6. 用这个代码来当作示例，就是：

# "我爱你"					"ich mochte ein bier P"
# "S I LOVE YOU"		"S i want a beer"
# "I LOVE YOU E"		"i want a beer E"
1
2
3

• 第二个问题：
  1. S代表start
  2. E代表end
  3. P代表的是一个pad字符（因为一个batch中句子长度可能不一样，所以就要规定一个最大长度max length，大于的就截断，小于的就使用特殊字符来填充，也就是P，如下图：）

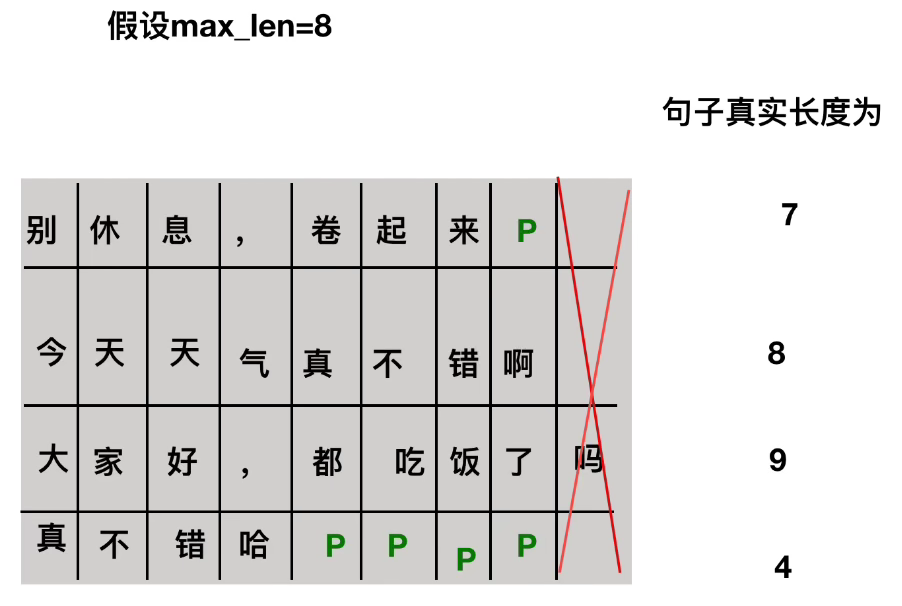
不想写了，看视频或者自己调试一下代码就知道了

4.3. 代码

"""
orginal from ：
https://github.com/graykode/nlp-tutorial/blob/master/5-1.Transformer/Transformer.ipynb
"""
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
import math


def make_batch(sentences):
    input_batch = [[src_vocab[n] for n in sentences[0].split()]]
    output_batch = [[tgt_vocab[n] for n in sentences[1].split()]]
    target_batch = [[tgt_vocab[n] for n in sentences[2].split()]]
    return torch.LongTensor(input_batch), torch.LongTensor(output_batch), torch.LongTensor(target_batch)



## 10
def get_attn_subsequent_mask(seq):
    """
    seq: [batch_size, tgt_len]
    """
    attn_shape = [seq.size(0), seq.size(1), seq.size(1)]
    # attn_shape: [batch_size, tgt_len, tgt_len]
    subsequence_mask = np.triu(np.ones(attn_shape), k=1)  # 生成一个上三角矩阵
    subsequence_mask = torch.from_numpy(subsequence_mask).byte()
    return subsequence_mask  # [batch_size, tgt_len, tgt_len]


## 7. ScaledDotProductAttention
class ScaledDotProductAttention(nn.Module):
    def __init__(self):
        super(ScaledDotProductAttention, self).__init__()

    def forward(self, Q, K, V, attn_mask):
        ## 输入进来的维度分别是 [batch_size x n_heads x len_q x d_k]  K： [batch_size x n_heads x len_k x d_k]  V: [batch_size x n_heads x len_k x d_v]
        ##首先经过matmul函数得到的scores形状是 : [batch_size x n_heads x len_q x len_k]
        scores = torch.matmul(Q, K.transpose(-1, -2)) / np.sqrt(d_k)

        ## 然后关键词地方来了，下面这个就是用到了我们之前重点讲的attn_mask，把被mask的地方置为无限小，softmax之后基本就是0，对q的单词不起作用
        scores.masked_fill_(attn_mask, -1e9) # Fills elements of self tensor with value where mask is one.
        attn = nn.Softmax(dim=-1)(scores)
        context = torch.matmul(attn, V)
        return context, attn


## 6. MultiHeadAttention
class MultiHeadAttention(nn.Module):
    def __init__(self):
        super(MultiHeadAttention, self).__init__()
        ## 输入进来的QKV是相等的，我们会使用映射linear做一个映射得到参数矩阵Wq, Wk,Wv
        self.W_Q = nn.Linear(d_model, d_k * n_heads)
        self.W_K = nn.Linear(d_model, d_k * n_heads)
        self.W_V = nn.Linear(d_model, d_v * n_heads)
        self.linear = nn.Linear(n_heads * d_v, d_model)
        self.layer_norm = nn.LayerNorm(d_model)

    def forward(self, Q, K, V, attn_mask):

        ## 这个多头分为这几个步骤，首先映射分头，然后计算atten_scores，然后计算atten_value;
        ##输入进来的数据形状： Q: [batch_size x len_q x d_model], K: [batch_size x len_k x d_model], V: [batch_size x len_k x d_model]
        residual, batch_size = Q, Q.size(0)
        # (B, S, D) -proj-> (B, S, D) -split-> (B, S, H, W) -trans-> (B, H, S, W)

        ##下面这个就是先映射，后分头；一定要注意的是q和k分头之后维度是一致额，所以一看这里都是dk
        q_s = self.W_Q(Q).view(batch_size, -1, n_heads, d_k).transpose(1,2)  # q_s: [batch_size x n_heads x len_q x d_k]
        k_s = self.W_K(K).view(batch_size, -1, n_heads, d_k).transpose(1,2)  # k_s: [batch_size x n_heads x len_k x d_k]
        v_s = self.W_V(V).view(batch_size, -1, n_heads, d_v).transpose(1,2)  # v_s: [batch_size x n_heads x len_k x d_v]

        ## 输入进行的attn_mask形状是 batch_size x len_q x len_k，然后经过下面这个代码得到 新的attn_mask : [batch_size x n_heads x len_q x len_k]，就是把pad信息重复了n个头上
        attn_mask = attn_mask.unsqueeze(1).repeat(1, n_heads, 1, 1)


        ##然后我们计算 ScaledDotProductAttention 这个函数，去7.看一下
        ## 得到的结果有两个：context: [batch_size x n_heads x len_q x d_v], attn: [batch_size x n_heads x len_q x len_k]
        context, attn = ScaledDotProductAttention()(q_s, k_s, v_s, attn_mask)
        context = context.transpose(1, 2).contiguous().view(batch_size, -1, n_heads * d_v) # context: [batch_size x len_q x n_heads * d_v]
        output = self.linear(context)
        return self.layer_norm(output + residual), attn # output: [batch_size x len_q x d_model]


## 8. PoswiseFeedForwardNet
class PoswiseFeedForwardNet(nn.Module):
    def __init__(self):
        super(PoswiseFeedForwardNet, self).__init__()
        self.conv1 = nn.Conv1d(in_channels=d_model, out_channels=d_ff, kernel_size=1)
        self.conv2 = nn.Conv1d(in_channels=d_ff, out_channels=d_model, kernel_size=1)
        self.layer_norm = nn.LayerNorm(d_model)

    def forward(self, inputs):
        residual = inputs # inputs : [batch_size, len_q, d_model]
        output = nn.ReLU()(self.conv1(inputs.transpose(1, 2)))
        output = self.conv2(output).transpose(1, 2)
        return self.layer_norm(output + residual)



## 4. get_attn_pad_mask

## 比如说，我现在的句子长度是5，在后面注意力机制的部分，我们在计算出来QK转置除以根号之后，softmax之前，我们得到的形状
## len_input * len*input  代表每个单词对其余包含自己的单词的影响力

## 所以这里我需要有一个同等大小形状的矩阵，告诉我哪个位置是PAD部分，之后在计算计算softmax之前会把这里置为无穷大；

## 一定需要注意的是这里得到的矩阵形状是batch_size x len_q x len_k，我们是对k中的pad符号进行标识，并没有对k中的做标识，因为没必要

## seq_q 和 seq_k 不一定一致，在交互注意力，q来自解码端，k来自编码端，所以告诉模型编码这边pad符号信息就可以，解码端的pad信息在交互注意力层是没有用到的；

def get_attn_pad_mask(seq_q, seq_k):
    batch_size, len_q = seq_q.size()
    batch_size, len_k = seq_k.size()
    # eq(zero) is PAD token
    pad_attn_mask = seq_k.data.eq(0).unsqueeze(1)  # batch_size x 1 x len_k, one is masking
    return pad_attn_mask.expand(batch_size, len_q, len_k)  # batch_size x len_q x len_k


## 3. PositionalEncoding 代码实现
class PositionalEncoding(nn.Module):
    def __init__(self, d_model, dropout=0.1, max_len=5000):
        super(PositionalEncoding, self).__init__()

        ## 位置编码的实现其实很简单，直接对照着公式去敲代码就可以，下面这个代码只是其中一种实现方式；
        ## 从理解来讲，需要注意的就是偶数和奇数在公式上有一个共同部分，我们使用log函数把次方拿下来，方便计算；
        ## pos代表的是单词在句子中的索引，这点需要注意；比如max_len是128个，那么索引就是从0，1，2，...,127
        ##假设我的demodel是512，2i那个符号中i从0取到了255，那么2i对应取值就是0,2,4...510
        self.dropout = nn.Dropout(p=dropout)

        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)## 这里需要注意的是pe[:, 0::2]这个用法，就是从0开始到最后面，补长为2，其实代表的就是偶数位置
        pe[:, 1::2] = torch.cos(position * div_term)##这里需要注意的是pe[:, 1::2]这个用法，就是从1开始到最后面，补长为2，其实代表的就是奇数位置
        ## 上面代码获取之后得到的pe:[max_len*d_model]

        ## 下面这个代码之后，我们得到的pe形状是：[max_len*1*d_model]
        pe = pe.unsqueeze(0).transpose(0, 1)

        self.register_buffer('pe', pe)  ## 定一个缓冲区，其实简单理解为这个参数不更新就可以

    def forward(self, x):
        """
        x: [seq_len, batch_size, d_model]
        """
        x = x + self.pe[:x.size(0), :]
        return self.dropout(x)


## 5. EncoderLayer ：包含两个部分，多头注意力机制和前馈神经网络
class EncoderLayer(nn.Module):
    def __init__(self):
        super(EncoderLayer, self).__init__()
        self.enc_self_attn = MultiHeadAttention()
        self.pos_ffn = PoswiseFeedForwardNet()

    def forward(self, enc_inputs, enc_self_attn_mask):
        ## 下面这个就是做自注意力层，输入是enc_inputs，形状是[batch_size x seq_len_q x d_model] 需要注意的是最初始的QKV矩阵是等同于这个输入的，去看一下enc_self_attn函数 6.
        enc_outputs, attn = self.enc_self_attn(enc_inputs, enc_inputs, enc_inputs, enc_self_attn_mask) # enc_inputs to same Q,K,V
        enc_outputs = self.pos_ffn(enc_outputs) # enc_outputs: [batch_size x len_q x d_model]
        return enc_outputs, attn


## 2. Encoder 部分包含三个部分：词向量embedding，位置编码部分，注意力层及后续的前馈神经网络

class Encoder(nn.Module):
    def __init__(self):
        super(Encoder, self).__init__()
        self.src_emb = nn.Embedding(src_vocab_size, d_model)  ## 这个其实就是去定义生成一个矩阵，大小是 src_vocab_size * d_model
        self.pos_emb = PositionalEncoding(d_model) ## 位置编码情况，这里是固定的正余弦函数，也可以使用类似词向量的nn.Embedding获得一个可以更新学习的位置编码
        self.layers = nn.ModuleList([EncoderLayer() for _ in range(n_layers)]) ## 使用ModuleList对多个encoder进行堆叠，因为后续的encoder并没有使用词向量和位置编码，所以抽离出来；

    def forward(self, enc_inputs):
        ## 这里我们的 enc_inputs 形状是： [batch_size x source_len]

        ## 下面这个代码通过src_emb，进行索引定位，enc_outputs输出形状是[batch_size, src_len, d_model]
        enc_outputs = self.src_emb(enc_inputs)

        ## 这里就是位置编码，把两者相加放入到了这个函数里面，从这里可以去看一下位置编码函数的实现；3.
        enc_outputs = self.pos_emb(enc_outputs.transpose(0, 1)).transpose(0, 1)

        ##get_attn_pad_mask是为了得到句子中pad的位置信息，给到模型后面，在计算自注意力和交互注意力的时候去掉pad符号的影响，去看一下这个函数 4.
        enc_self_attn_mask = get_attn_pad_mask(enc_inputs, enc_inputs)
        enc_self_attns = []
        for layer in self.layers:
            ## 去看EncoderLayer 层函数 5.
            enc_outputs, enc_self_attn = layer(enc_outputs, enc_self_attn_mask)
            enc_self_attns.append(enc_self_attn)
        return enc_outputs, enc_self_attns

## 10.
class DecoderLayer(nn.Module):
    def __init__(self):
        super(DecoderLayer, self).__init__()
        self.dec_self_attn = MultiHeadAttention()
        self.dec_enc_attn = MultiHeadAttention()
        self.pos_ffn = PoswiseFeedForwardNet()

    def forward(self, dec_inputs, enc_outputs, dec_self_attn_mask, dec_enc_attn_mask):
        dec_outputs, dec_self_attn = self.dec_self_attn(dec_inputs, dec_inputs, dec_inputs, dec_self_attn_mask)
        dec_outputs, dec_enc_attn = self.dec_enc_attn(dec_outputs, enc_outputs, enc_outputs, dec_enc_attn_mask)
        dec_outputs = self.pos_ffn(dec_outputs)
        return dec_outputs, dec_self_attn, dec_enc_attn

## 9. Decoder

class Decoder(nn.Module):
    def __init__(self):
        super(Decoder, self).__init__()
        self.tgt_emb = nn.Embedding(tgt_vocab_size, d_model)
        self.pos_emb = PositionalEncoding(d_model)
        self.layers = nn.ModuleList([DecoderLayer() for _ in range(n_layers)])

    def forward(self, dec_inputs, enc_inputs, enc_outputs): # dec_inputs : [batch_size x target_len]
        dec_outputs = self.tgt_emb(dec_inputs)  # [batch_size, tgt_len, d_model]
        dec_outputs = self.pos_emb(dec_outputs.transpose(0, 1)).transpose(0, 1) # [batch_size, tgt_len, d_model]

        ## get_attn_pad_mask 自注意力层的时候的pad 部分
        dec_self_attn_pad_mask = get_attn_pad_mask(dec_inputs, dec_inputs)

        ## get_attn_subsequent_mask 这个做的是自注意层的mask部分，就是当前单词之后看不到，使用一个上三角为1的矩阵
        dec_self_attn_subsequent_mask = get_attn_subsequent_mask(dec_inputs)

        ## 两个矩阵相加，大于0的为1，不大于0的为0，为1的在之后就会被fill到无限小
        dec_self_attn_mask = torch.gt((dec_self_attn_pad_mask + dec_self_attn_subsequent_mask), 0)


        ## 这个做的是交互注意力机制中的mask矩阵，enc的输入是k，我去看这个k里面哪些是pad符号，给到后面的模型；注意哦，我q肯定也是有pad符号，但是这里我不在意的，之前说了好多次了哈
        dec_enc_attn_mask = get_attn_pad_mask(dec_inputs, enc_inputs)

        dec_self_attns, dec_enc_attns = [], []
        for layer in self.layers:
            dec_outputs, dec_self_attn, dec_enc_attn = layer(dec_outputs, enc_outputs, dec_self_attn_mask, dec_enc_attn_mask)
            dec_self_attns.append(dec_self_attn)
            dec_enc_attns.append(dec_enc_attn)
        return dec_outputs, dec_self_attns, dec_enc_attns


## 1. 从整体网路结构来看，分为三个部分：编码层，解码层，输出层
class Transformer(nn.Module):
    def __init__(self):
        super(Transformer, self).__init__()
        self.encoder = Encoder()  ## 编码层
        self.decoder = Decoder()  ## 解码层
        self.projection = nn.Linear(d_model, tgt_vocab_size, bias=False) ## 输出层 d_model 是我们解码层每个token输出的维度大小，之后会做一个 tgt_vocab_size 大小的softmax
    def forward(self, enc_inputs, dec_inputs):
        ## 这里有两个数据进行输入，一个是enc_inputs 形状为[batch_size, src_len]，主要是作为编码段的输入，一个dec_inputs，形状为[batch_size, tgt_len]，主要是作为解码端的输入

        ## enc_inputs作为输入 形状为[batch_size, src_len]，输出由自己的函数内部指定，想要什么指定输出什么，可以是全部tokens的输出，可以是特定每一层的输出；也可以是中间某些参数的输出；
        ## enc_outputs就是主要的输出，enc_self_attns这里没记错的是QK转置相乘之后softmax之后的矩阵值，代表的是每个单词和其他单词相关性；
        enc_outputs, enc_self_attns = self.encoder(enc_inputs)

        ## dec_outputs 是decoder主要输出，用于后续的linear映射； dec_self_attns类比于enc_self_attns 是查看每个单词对decoder中输入的其余单词的相关性；dec_enc_attns是decoder中每个单词对encoder中每个单词的相关性；
        dec_outputs, dec_self_attns, dec_enc_attns = self.decoder(dec_inputs, enc_inputs, enc_outputs)

        ## dec_outputs做映射到词表大小
        dec_logits = self.projection(dec_outputs) # dec_logits : [batch_size x src_vocab_size x tgt_vocab_size]
        return dec_logits.view(-1, dec_logits.size(-1)), enc_self_attns, dec_self_attns, dec_enc_attns



if __name__ == '__main__':

    ## 句子的输入部分，
    sentences = ['ich mochte ein bier P', 'S i want a beer', 'i want a beer E']


    # Transformer Parameters
    # Padding Should be Zero
    ## 构建词表
    src_vocab = {'P': 0, 'ich': 1, 'mochte': 2, 'ein': 3, 'bier': 4}
    src_vocab_size = len(src_vocab)

    tgt_vocab = {'P': 0, 'i': 1, 'want': 2, 'a': 3, 'beer': 4, 'S': 5, 'E': 6}
    tgt_vocab_size = len(tgt_vocab)

    src_len = 5 # length of source
    tgt_len = 5 # length of target

    ## 模型参数
    d_model = 512  # Embedding Size
    d_ff = 2048  # FeedForward dimension
    d_k = d_v = 64  # dimension of K(=Q), V
    n_layers = 6  # number of Encoder of Decoder Layer
    n_heads = 8  # number of heads in Multi-Head Attention

    model = Transformer()

    criterion = nn.CrossEntropyLoss()
    optimizer = optim.Adam(model.parameters(), lr=0.001)

    enc_inputs, dec_inputs, target_batch = make_batch(sentences)

    for epoch in range(20):
        optimizer.zero_grad()
        outputs, enc_self_attns, dec_self_attns, dec_enc_attns = model(enc_inputs, dec_inputs)
        loss = criterion(outputs, target_batch.contiguous().view(-1))
        print('Epoch:', '%04d' % (epoch + 1), 'cost =', '{:.6f}'.format(loss))
        loss.backward()
        optimizer.step()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301