- 1解决Untracked Files Prevent Checkout问题
- 2GPT2代码运行,个人文本生成助手,不依赖OpenAI API调用
- 3【智慧农业】智能灌溉系统应用方案_智慧农业喷淋灌溉项目方案
- 4【提效】让GPT帮你写爬虫程序,不懂爬虫也能行_如何用gpt写爬虫
- 5【网络安全】2024年热门网络安全运营工具/方案推荐_网络安全运营产品
- 6知识图谱---Neo4J篇_neo4j知识图谱
- 7【Shell编程】Shell中for循环、while循环、until循环语句_shell编程for
- 8在小程序中使用formdata上传数据,可实现多文件上传
- 9A Comprehensive Survey on Graph Neural Networks(2020 Trans)_complex-valued neural networks: a comprehensive su
- 10【ROS笔记本】ROS代码编写知识_getnumpublishers();
【PID控制原理及其算法】_pid算法原理
赞
踩
前言
本文以自己的学习过程总结而来,将自己的经验写出来以供大家一起学习,如有错误请多指教
一、PID是什么?
PID就是比例、积分、微分,PID算法可以说是在自动控制原理中比较经典的一套算法,在现实生活中应用比较广泛。
二、PID原理
常规的模拟 PID 控制系统原理框图如下图所示:

从上图可以发现,这是一个闭环控制系统,由PID控制器、传感器、被控对象构成。
被控对象的输出就是系统的输出,而系统的输出会被传感器传感,传感器会输出反馈信号给输入;
给定输入和反馈输入经过比较之后会产生一个误差(偏差),这个误差就是PID控制器的输入;pid控制器经过运算处理之后会输出控制量(或控制量的增量)给到执行机构(上图中没有画出执行机构),从而改变被控对象的输出。
- 1
- 2
- 3
那么使用PID的目的是什么呢?
我的理解是快速调节系统,最终让系统的输出和给定输入保持一致。
PID的控制环节和参数
既然要使用PID控制器,那么肯定要涉及到三个重要环节及其参数:
| 环节 | 参数 |
|---|---|
| 比例 | Kp |
| 积分 | Ti |
| 微分 | Td |
注:Kp是比例系数,Ti是积分常数,Td是微分常数
- 1
下面介绍每个环节的作用
比例环节
比例环节的作用是对偏差瞬间作出反应。偏差一旦产生控制器立即产生控制作用, 使控制量向减少偏差的方向变化。 控制作用的强弱取决于比例系数Kp, 比例系数Kp越大,控制作用越强, 则过渡过程越快, 控制过程的静态偏差也就越小; 但是Kp越大,也越容易产生振荡, 破坏系统的稳定性。 故而, 比例系数Kp选择必须恰当, 才能过渡时间少, 静差小而又稳定的效果。
积分环节
从积分部分的数学表达式可以知道, 只要存在偏差, 则它的控制作用就不断的增加; 只有在偏差e(t)=0时, 它的积分才能是一个常数,控制作用才是一个不会增加的常数。 可见,积分部分可以消除系统的偏差。
积分环节的调节作用虽然会消除静态误差,但也会降低系统的响应速度,增加系统的超调量。积分常数Ti越大,积分的积累作用越弱,这时系统在过渡时不会产生振荡; 但是增大积分常数Ti会减慢静态误差的消除过程,消除偏差所需的时间也较长, 但可以减少超调量,提高系统的稳定性。
当 Ti 较小时, 则积分的作用较强,这时系统过渡时间中有可能产生振荡,不过消除偏差所需的时间较短。所以必须根据实际控制的具体要求来确定Ti 。
微分环节
实际的控制系统除了希望消除静态误差外,还要求加快调节过程。在偏差出现的瞬间,或在偏差变化的瞬间, 不但要对偏差量做出立即响应(比例环节的作用), 而且要根据偏差的变化趋势预先给出适当的纠正。为了实现这一作用,可在 PI 控制器的基础上加入微分环节,形成 PID 控制器。
微分环节的作用使阻止偏差的变化。它是根据偏差的变化趋势(变化速度)进行控制。偏差变化的越快,微分控制器的输出就越大,并能在偏差值变大之前进行修正。微分作用的引入, 将有助于减小超调量, 克服振荡, 使系统趋于稳定, 特别对髙阶系统非常有利, 它加快了系统的跟踪速度。但微分的作用对输入信号的噪声很敏感,对那些噪声较大的系统一般不用微分, 或在微分起作用之前先对输入信号进行滤波。
总结特点
| 环节 | 特点 |
|---|---|
| 比例 | 偏差一产生,控制器立即做出响应,产生控制作用,使控制量向减少偏差的方向变化 |
| 积分 | 消除系统的静态误差;但同时会降低系统的响应速度,增加超调量;积分时间越长,积分的积累作用越弱,消除静态误差的时间会变长;但系统过渡时不会产生振荡,可以减少超调量,提高系统的稳定性 |
| 微分 | 加快调节过程,阻止偏差的变化;有助于减少超调量,克服振荡,使系统趋于稳定 |
三、PID的分类
PID分为数字PID和模拟PID。
模拟PID
模拟PID控制系统的原理框图如下图所示:

r(t)是给定输入,e(t)是偏差,u(t)是控制器的输出,y(t)是被控对象的输出。
模拟PID控制器的控制规律如下:

把上面这个数学表达式剖开,
比例部分:
Kp * e(t)
- 1
积分部分:

微分部分:

数字PID
- 位置型PID算法
pid算法的数学表达式如下表达式1:

(表达式1)
将其离散化,以T作为采样周期,上述表达式可变为表达式2:

(表达式2)
把表达式2中的参数整定后得到下面的表达式3:
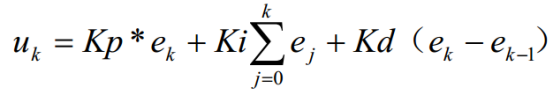
(表达式3)
上面的表达式中:
k ―― 采样序号, k =0, 1, 2,……;
uk ―― 第 k 次采样时刻的计算机输出值;
e(k) ―― 第 k 次采样时刻输入的偏差值;
e(k-1) ―― 第 k -1 次采样时刻输入的偏差值;
Ki ――积分系数, Ki=Kp *T / Ti ;
Kd ――微分系数, Kd=Kp *Td / T ;
- 增量型PID算法
既然u(k)的表达式确定了,那么把u(k) 减去u(k-1)就可以得到控制量的增量,所以得到的数学表达式如下:

其中,



不同PID算法的特点
| 算法 | 特点 1 |
|---|---|
| 位置型 | 位置式PID控制的输出与整个过去的状态有关,用到了误差的累加值 |
| 增量型 | 增量式PID的输出只与当前拍和前两拍的误差有关,因此位置式PID控制的累积误差相对更大 |
| 算法 | 特点 2 |
|---|---|
| 位置型 | 位置式PID适用于执行机构不带积分部件的对象,如电液伺服阀 |
| 增量型 | 增量式PID控制输出的是控制量增量,并无积分作用,因此该方法适用于执行机构带积分部件的对象,如步进电机 |
| 算法 | 特点 3 |
|---|---|
| 位置型 | 位置式的输出直接对应对象的输出,因此对系统影响较大 |
| 增量型 | 由于增量式PID输出的是控制量增量,如果计算机出现故障,误动作影响较小,而执行机构本身有记忆功能,可仍保持原位,不会严重影响系统的工作 |
四、PID代码实现
位置型PID算法
源码如下:
//位置型PID算法源码
typedef struct
{
float Kp; //比例系数Proportional
float Ki; //积分系数Integral
float Kd; //微分系数Derivative
float Ek; //当前误差
float Ek1; //前一次误差 e(k-1)
float Ek2; //再前一次误差 e(k-2)
float LocSum; //累计积分位置
}PID_LocTypeDef;
/************************************************
函数名称 : PID_Loc
功 能 : PID位置(Location)计算
参 数 : SetValue ------ 给定值(期望值)
ActualValue --- 实际值(反馈值)
PID ----------- PID数据结构
返 回 值 : PIDLoc -------- PID位置
*************************************************/
float PID_Loc(float SetValue, float ActualValue, PID_LocTypeDef *PID)
{
float PIDLoc; //位置
PID->Ek = SetValue - ActualValue;
PID->LocSum += PID->Ek; //累计误差
PIDLoc = PID->Kp * PID->Ek + (PID->Ki * PID->LocSum) + PID->Kd * (PID->Ek - PID->Ek1);
PID->Ek1 = PID->Ek;
return PIDLoc;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
上面代码中的Kp是指比例系数;
Ki = Kp * T / Ti;
Kd = Kp * Td / T。
增量型PID算法
源码如下:
//增量型pid算法
typedef struct
{
float Kp; //比例系数Proportional
float Ki; //积分系数Integral
float Kd; //微分系数Derivative
float Ek; //当前误差
float Ek1; //前一次误差 e(k-1)
float Ek2; //再前一次误差 e(k-2)
}PID_IncTypeDef;
/************************************************
函数名称 : PID_Inc
功 能 : PID增量(Increment)计算
参 数 : SetValue ------ 设置值(期望值)
ActualValue --- 实际值(反馈值)
PID ----------- PID数据结构
返 回 值 : PIDInc -------- 本次PID增量(+/-)
*************************************************/
float PID_Inc(float SetValue, float ActualValue, PID_IncTypeDef *PID)
{
float PIDInc; //增量
PID->Ek = SetValue - ActualValue;
PIDInc = (PID->Kp * PID->Ek) - (PID->Ki * PID->Ek1) + (PID->Kd * PID->Ek2); //参数已做整定
PID->Ek2 = PID->Ek1;
PID->Ek1 = PID->Ek;
return PIDInc;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
在上面代码中:(参数是经过整定的)
实际上:
Kp = KP + KI + KD;
Ki = KP + 2 * KD;
KD = KD;
而KP就是比例系数
KI = KP * T / Ti; //Ti是指积分时间
KD = KP * Td / Ti //Td是指微分时间
总结
以上就是今天要讲的内容,本文简单介绍了PID的概念、PID的控制原理,以及介绍了PID不同算法的特点及其示例源码


