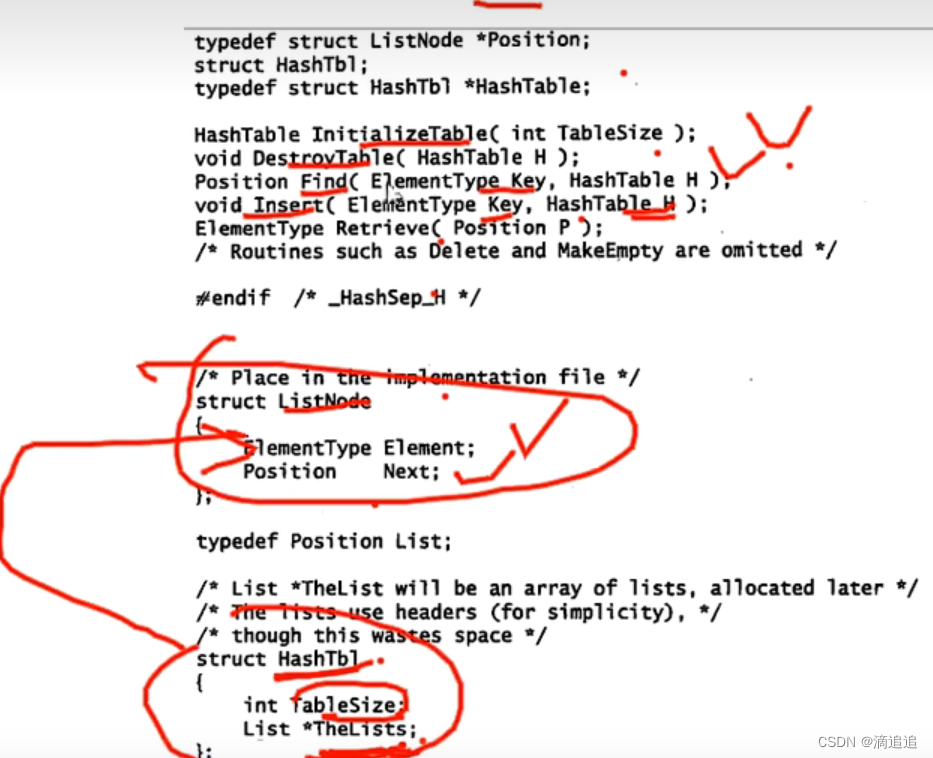
【无标题】_4阶b树必须存在有四个孩子的结点吗

运行时间中的对数：

1, 如果一个算法用常数时间O(1)将问题的大小削减为其一部分(比如1/2)那么该算法就是O(log N)因为

log2 1000 = x转换成2的x次方=1000 算的x是指数所以不会很大

2, 另一方面如果使用常数时间只是把问题减少一个常数（如将问题减少1）那么这种算法就是O(N)

类似于忽略常数

对分查找就是上面的第一种实例

数组的删除要把后面的元素全部往前移动一位，要花费O（N）的时间、

而链表只需要删掉结点把指针指向下一个

插入要使用一次malloc调用获得一个新单元

数组和链表的区别：

1，链表是不连续存储的

2，链表的插入和删除效率高

3，链表的查找位置效率比数组低

4，链表的大小是不固定的只要内存够就可以动态加减

树的内容

 B树数据都存在叶子结点，非叶子结点都叫做内部节点

4阶B-树又称2-3-4因为这棵树最多只能有4个孩子结点，如果插入时超过了最大存储关键值，那就新建一个结点。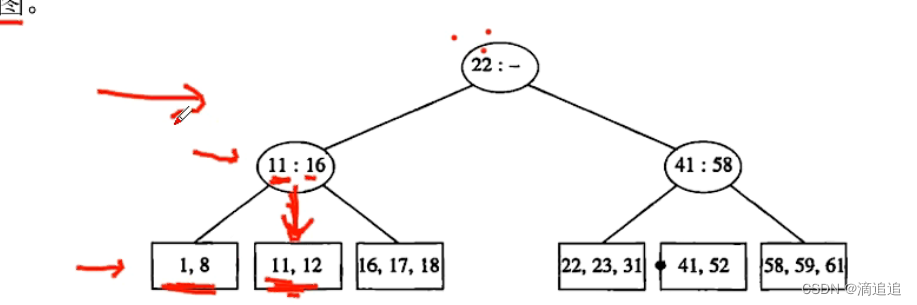

 

 

 

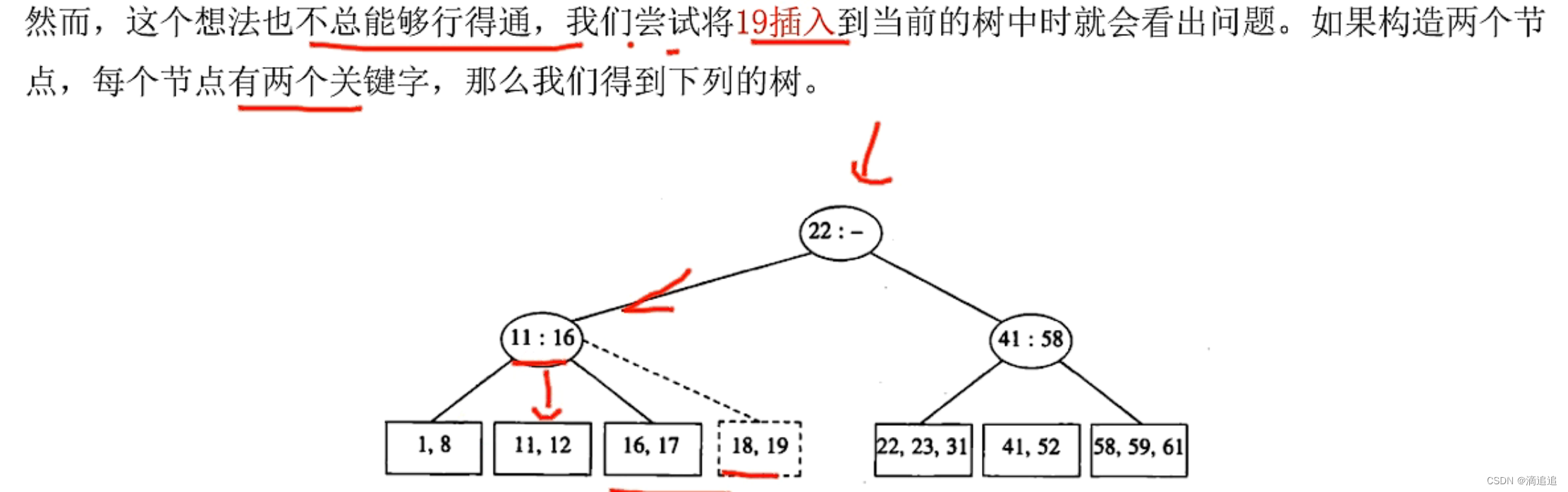
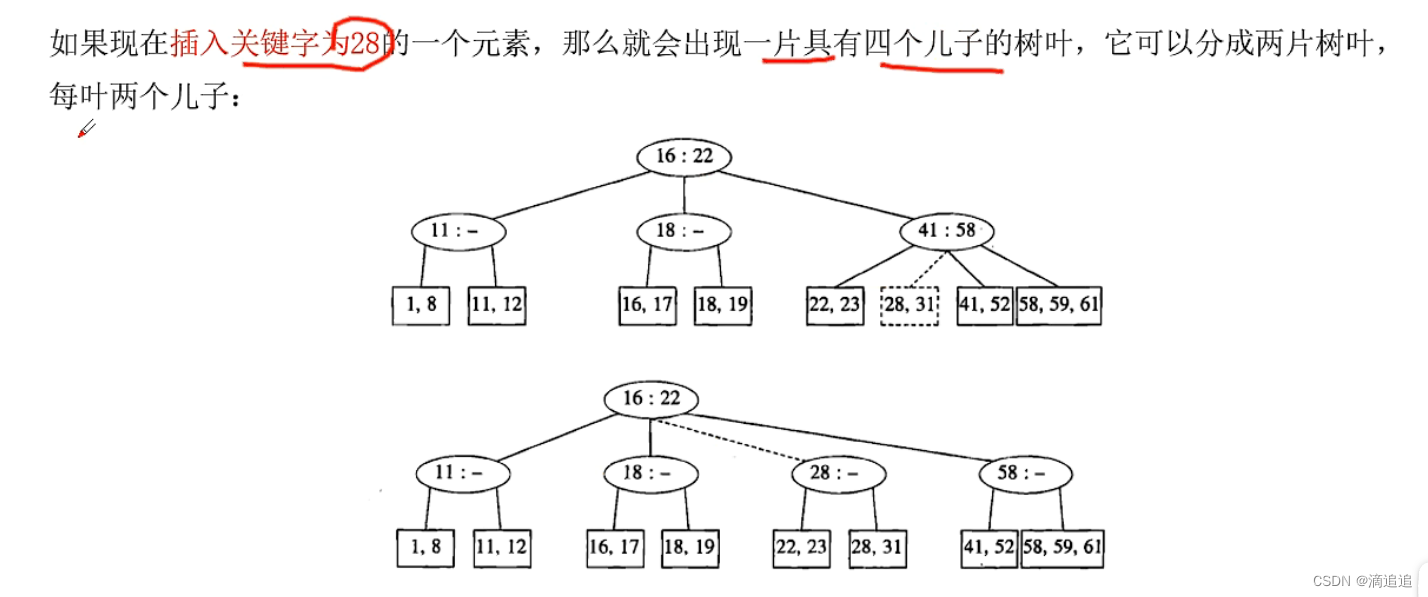
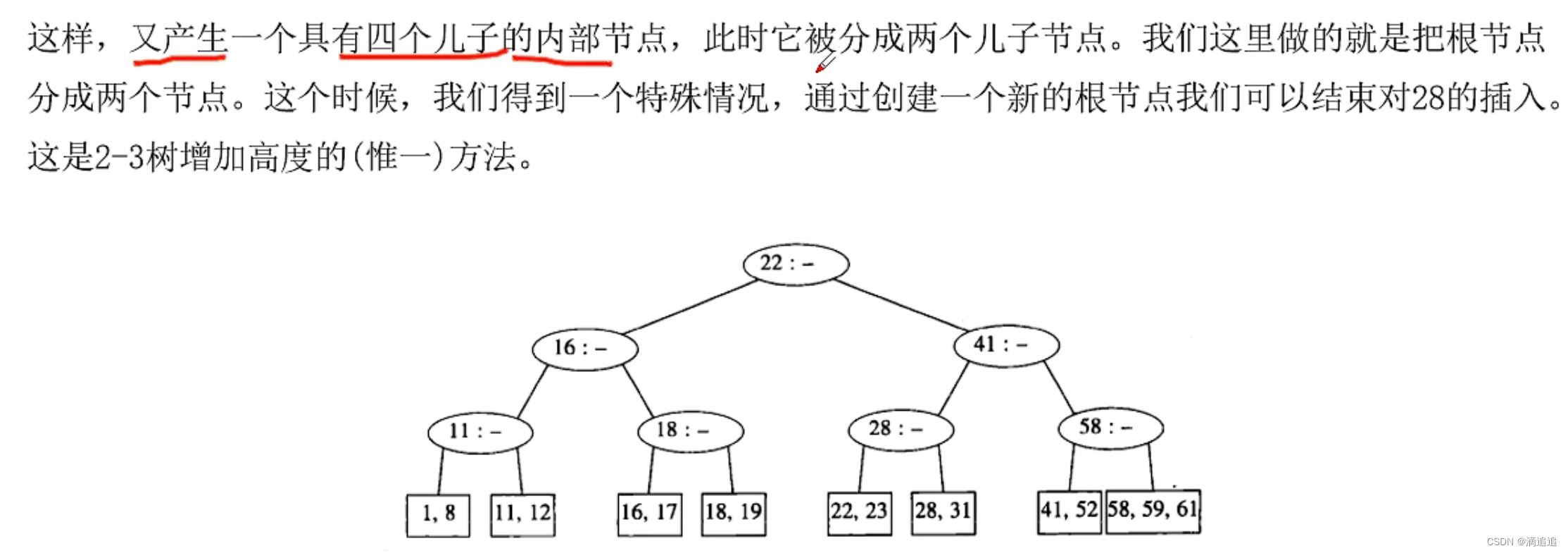
以上是满足2-3树条件的插入过程

数据库永B+存储的好处是可以降低数的高度

B树2-3-4树除了根节点外都至少要有2个孩子

在删除的时候我们可以通过查找到要被删除的关键字并将其除去完成删除，如果这个关键字是节点的两个关键字的其中一个，除去后只剩下一个关键字，那就不满足2-3-4树的要求了，此时可以把关键字与兄弟节点结合，如果结合成功后这两个节点的父亲失去了一个孩子，那么这个父亲也只剩下一个孩子了，不符合2-3-4树的要求，所以这个根也要去删除，而树减少了一层，当我们合并节点时，记得更新保存内部节点的信息。

总结

查找树在算法设计中十分重要，其对数的开销很小，但是问题时过于依赖输入。如果输入的N过大或者过小，查找树会成为昂贵的链表，AVL树要求所有节点的左子树和右子树的高度最多相差1，不改变树的操作都可以用查找树的程序，改变树的操作需要将树恢复，比如插入和删除。

伸展树的节点可以达到任意深度，但每次访问后都将节点移动到根部，所以实际效果是花费O（MlogN）时间，与平衡树花费的时间相同。

B-树的平衡M-路树，意思是最多有M个孩子，能很好的匹配磁盘，且B-树都是有序的。不过实践中，所有平衡树都不如简单二叉查找树省时，不过一般来说是可以接受的

B-树的M再增大的时候插入和删除的时间就会增长

最后注意，通过将一些元素插入到查找树中并进行中序遍历，得到的便是从小到大排序过的元素，

中序遍历就是先打印左节点再打印根节点再打印右节点，先序遍历和后序遍历以此类推。

B树实际用于数据库

散列（哈希表）

散列是一种以常数时间进行插入，删除，查找的技术

是一种无序的数据结构，因此查找最大值最小值和进行有序打印也是不支持的

理想的散列表只是一个拥有关键字和固定大小的数组表的大小用TableSize来记录

通常习惯让表从0到TableSize-1来变化

散列函数:

每一个关键词被映射到0到TableSize-1中的某个数，并放到对应的单元，这就叫做散列函数。

给这个函数传参，会返回对应的角标并存在里面，函数要在单元内均匀的分配关键字

通常分配的方法是Key mod TableSize但如果遇到比如表的大小为10而关键字的个位数都是0，那么这种情况的散列函数就要仔细考虑，否则可能会重复占用角标为0的位置，好的方法是保证表的大小是素数

哈希表分配到同一个角标从而发生冲突是不能避免的，要尽量防止出现这种情况

字符串散列函数:

一种方法是把字符串中的ASCII码值加起来再 mod 与TableSize

 但是如果表很大，该函数不会很好的分配关键字,因为 mod 会得到数本身，而ASCII码值加起来并不大导致剩下的空间没有被利用到。

解决冲突的方法有分离链接法和开放定址法

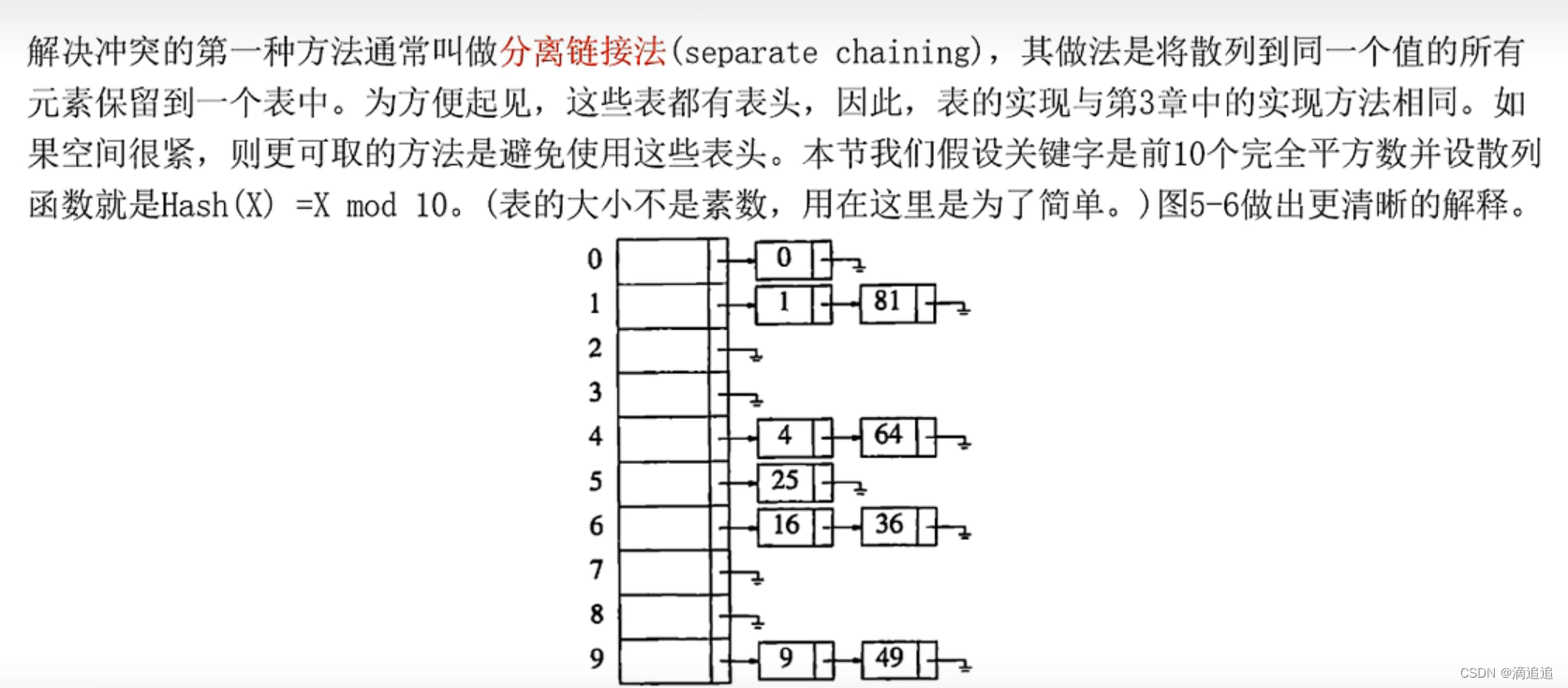
 本质上是数组+链表的实现

实际上数组里存的并不是数据，而是链表的哑结点(表头）