- 1spark学习笔记3(使用spark Sql进行离线数据分析项目数据的可视化、yarn运行、优化)_spark yarn 算子可视化
- 2深度学习中经典的时间序列预测项目
- 3vue-cron
- 4深度学习基础知识-误差反向传播+训练技巧(无代码仅用来理解)_反向传播训练
- 5MySQL中七个查询命令的优先级及特点_mysql分组排序条件查询谁先谁后
- 6生成对抗网络(GAN)在AI去衣技术中的创新应用与探索
- 7Selenium——基于Web的UI自动化测试工具(一)
- 8Word 2016 交叉引用 章节的题注与交叉引用_交叉引用找不到引用的题注
- 9C语言------冒泡法排序
- 104. Yolov8 Mosaic数据增强详解_yolov8数据增强
RS纠删码性能分析实战_rs 柯西矩阵
赞
踩
前言
Erasure Code(EC),即纠删码,是一种前向错误纠正技术(Forward Error Correction,FEC,说明见后附录)。目前很多用在分布式存储来提高存储的可靠性。相比于多副本技术而言,纠删码以最小的数据冗余度获得更高的数据可靠性,但是它的编码方式比较复杂。
目前纠删码分为三类:RS(Reed-solomon)纠删码、阵列纠删码和LDPC低密度奇偶校验纠删码。在这里我们就不对各类纠删码的具体实现原理进行讲解了,网上有太多理论讲解的文章。
本文对RS纠删码性能进行分析,分别从RS纠删码的编解码吞吐量、CPU占有、磁盘I/O方面进行分析。从范德蒙生成矩阵、柯西生成矩阵、柯西改进矩阵三类不断改进的方法改进基于RS的纠删码,改进的方式主要是简化生成矩阵从而降低矩阵求逆的代价,将RS的乘法进一步改为二进制与运算,加法改为异或运算。从实验的结果可以的出,编解码的效率都在不断提高;同时基于RS的纠删码,冗余块数是可以调整的,可以保证容错率。
性能分析运行环境
- CPU: Intel® Xeon® CPU E5-2603 0 @ 1.80GHz
- 内存:2049316 kB
- Linux版本:25~precise1-Ubuntu SMP Thu Jan 30 17:39:31 UTC 2014 x86_64
x86_64 x86_64 GNU/Linux
Reed_Sol_Van
基于原始范德蒙矩阵的RS纠删码,生成矩阵由范德蒙矩阵构造,将原始数据与生成矩阵相乘生成原始数据m块与冗余数据k块,在磁盘上丢失的数据小于k的情况下,通过生成矩阵与原始数据加冗余数据恢复数据。在原始数据为1G的条件下,将原始数据划分为10份,每份100M作为原始数据块,同时将冗余块的大小设置为100M,当冗余块从1增加到6块下的情况下,对于不同的冗余值下的编码与解码吞吐率。为降低计算复杂度,转换到伽罗华域中进行运算,将域中w设置为8、用于读取数据块大小packsize=1024、缓存设置buffersize=500000,程序处理packsize,会调整packsize到一个适当的大小;
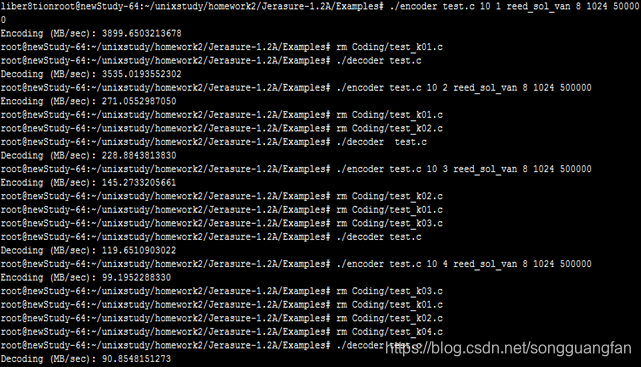
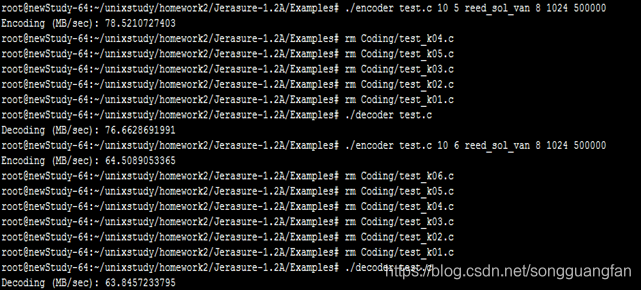
| 冗余块(100MB) | 编码吞吐(MB/sec) | 解码吞吐(MB/sec) |
|---|---|---|
| 1 | 3899.650321 | 3535.019355 |
| 2 | 271.0552987 | 228.8843814 |
| 3 | 145.2733206 | 119.6510903 |
| 4 | 99.19522883 | 90.85481513 |
| 5 | 78.52107274 | 76.6628692 |
| 6 | 64.50890534 | 63.84572338 |
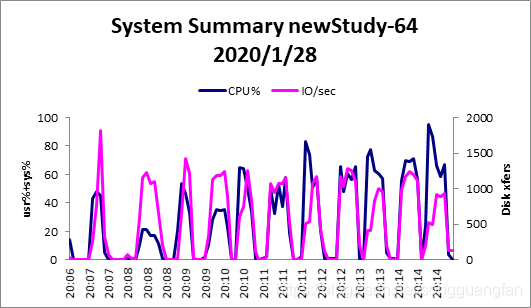
| Total System I/O Statistics | CPU: | User% | Sys% | Wait% | Idle% | CPU% | |
|---|---|---|---|---|---|---|---|
| Avg tps during an interval: | 520 | Avg | 17.6 | 9.5 | 23.2 | 49.6 | 27.1 |
| Max tps during an interval: | 1,820 | Max | 75.1 | 45.1 | 82.8 | 99.8 | |
| Max tps interval time: | 20:07:30 | Max:Avg | 4.3 | 4.7 | 3.6 | 2.0 | 3.5 |
| Total number of Mbytes read: | 22,718 | ||||||
| Total number of Mbytes written: | 39,303 | ||||||
| Read/Write Ratio: | 0.6 |
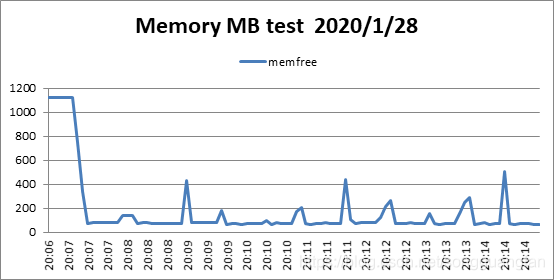
从编解码的吞吐率中可以得出随着冗余数据的增加,编码与解码的吞吐都在降低,冗余数据从200M增加到600M,编码吞吐从271.1MB/sec降低到64.5MB/sec,解码吞吐从228.9 MB/sec降低到63.8MB/sec,说明当冗余过多时无论是编码还是解码都会对吞吐性能造成影响,但同时冗余数据的增加可以提高可靠性,冗余越多,可靠性越高。同时对于cpu与I/O的考察可以得出,当冗余数据增加时,cpu的压力逐渐变大,从1块冗余到6块冗余,cpu的平均压力从40%增加到60%,I/O的压力则较为稳定。同时编码对cpu与I/O的压力要大于解码时的压力。对于内存的消耗同时比较稳定,编码维持在400M,解码维持在200M。在GF(2w)域上,将范德蒙矩阵进行初等变换,将其前n行变成一个单位矩阵,就可以得到满足RS编码要求的生成矩阵。在GF(2w)域上,加法的定义实际上就是异或,而乘法则复杂的多,通常便准的RS编码的计算开销太大,无法适应存储系统对于计算效率的要求。基于范德蒙矩阵的RS码是最早的RS纠删码,在理论上,复杂的乘法运算与矩阵求逆导致了计算的复杂,该方法不适合用于大数据量的文件,从实验的结果也可以得出伴随冗余的增加,由于矩阵求逆与乘法的复杂,导致编解码吞吐的下降。
Reed_Sol_R6_Op
一个磁盘冗余的RAID模型,是将假设有n个存储成员,把每个存储成员划分成若干个存储单元,其中n-1(D1…Di…Dn-1)个成员盘为数据,1个成员盘(p1)为校验。
D1 + D2 + D3 + … +Dn-1 = P1
Dx = P1 + D1 + D2 + D3 +… +Dn-1
如果需要设计一种存储模型,实现在缺失2个成员的情况下,存储整体依然可以运算完整,最好的数学模型恐怕就是二元一次方程了,形如下面方程组:
aX+bY=c
dX+eY=f。 其中a/d != b/e
上述方程式用到乘法与除法,同时,乘法与除法完全可逆,且满足交换律、结合律与分配率。还是在加法中遇到的困难,普通的数学乘法会导致校验容量的累加,所以不可取,基于伽罗华域的乘除法。
如果需要设计一种存储模型,实现在缺失2个成员的情况下,存储整体依然可以运算完整,最好的数学模型恐怕就是二元一次方程了,形如下面方程组:
aX+bY=c
dX+eY=f。 其中a/d != b/e
上述方程式用到乘法与除法,同时,乘法与除法完全可逆,且满足交换律、结合律与分配率。还是在加法中遇到的困难,普通的数学乘法会导致校验容量的累加,所以不可取,基于伽罗华域的乘除法。
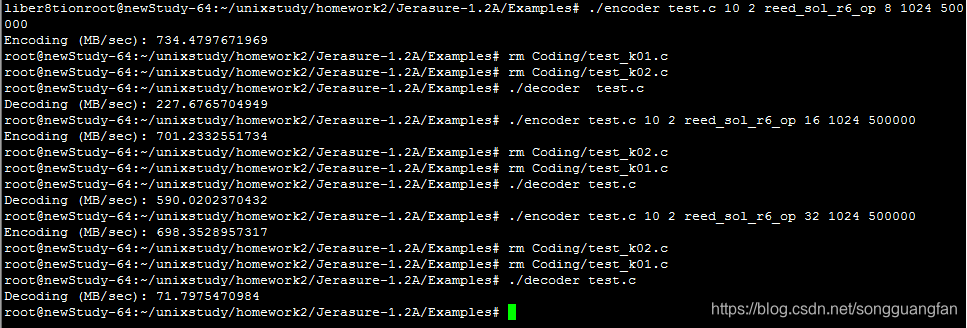
| w值 | 编码吞吐(MB/sec) | 解码吞吐(MB/sec) | 冗余(100MB) |
|---|---|---|---|
| 8 | 734.4797672 | 227.6765705 | 2 |
| 16 | 701.2332552 | 228.8843814 | 2 |
| 32 | 145.2733206 | 119.6510903 | 2 |
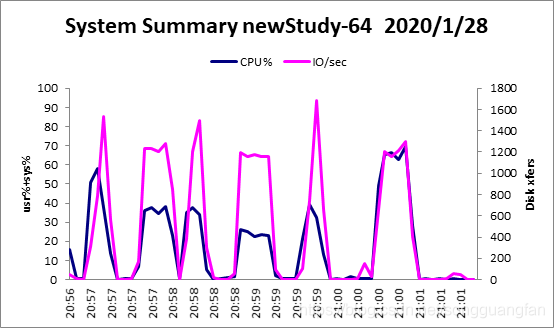
| Total System I/O Statistics | CPU: | User% | Sys% | Wait% | Idle% | CPU% | |
|---|---|---|---|---|---|---|---|
| Avg tps during an interval: | 469 | Avg | 8.6 | 8.9 | 21.9 | 60.6 | 17.4 |
| Max tps during an interval: | 1,687 | Max | 56.8 | 48.0 | 77.4 | 100.0 | 69.4 |
| Max tps interval time: | 20:59:53 | Max:Avg | 6.6 | 5.4 | 3.5 | 1.6 | 4.0 |
| Total number of Mbytes read: | 12,782 | ||||||
| Total number of Mbytes written: | 19,468 | ||||||
| Read/Write Ratio: | 0.7 |

RAID6编码生成2份冗余块,冗余量为200MB。而随着w值的增加,编解码吞吐都在下降,编码吞吐从734.4797672MB/sec降低到145.2733206MB/sec,解码吞吐从227.6765705 MB/sec降低到119.6510903 MB/sec。但较于基于范德蒙矩阵的矩阵生成方法确实编解码吞吐有较大提高。编解码cpu占有大概在40%左右,对于磁盘I/O吞吐也维持在600MB/sec上下,而内存则维持在200MB左右。RAID6是横式阵列码,计算过程全部采取异或方式,使得整体的性能有较好提高,同时冗余数据只能为2块,使得容错率降低。
Cauchy_Orig
采用范德蒙矩阵作为编码矩阵的问题在于算法复杂度太高,其解码算法复杂度为 O(n^3)。采用目前的处理器技术,还是会影响IO的性能,增加IO延迟。因此,找到一种更加合理的编码矩阵,降低算法复杂度是 Erasure code 得以广泛应用的一个前提条件。用柯西矩阵来代替范德蒙矩阵。由于范德蒙矩阵求逆运算的复杂度为O(n3),而柯西矩阵求逆运算的复杂度仅为O(n2)。因此,采用柯西矩阵可以降低解码的运算复杂度。采用有限域二进制矩阵的方式来提高运算效率,直接将乘法转换成XOR逻辑运算,大大降低了运算复杂度。
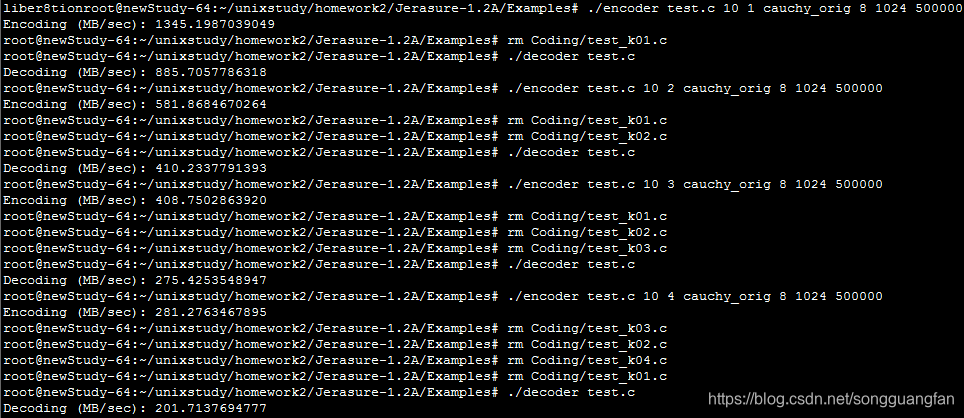
| 冗余块(100MB) | 编码吞吐(MB/sec) | 解码吞吐(MB/sec) |
|---|---|---|
| 1 | 1345.198704 | 885.7057786 |
| 2 | 581.868467 | 410.2337791 |
| 3 | 408.7502864 | 275.4253549 |
| 4 | 281.2763468 | 201.7137695 |
| 5 | 230.0346179 | 166.6484164 |
| 6 | 198.1768765 | 140.8307715 |
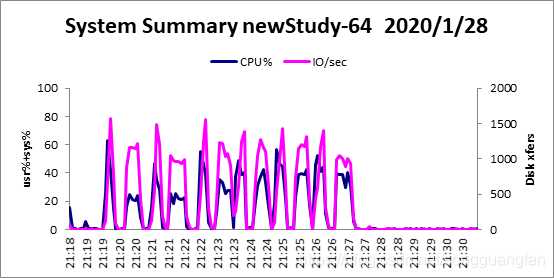
| Total System I/O Statistics | CPU: | User% | Sys% | Wait% | Idle% | CPU% |
|---|---|---|---|---|---|---|
| Avg tps during an interval: | 387 | Avg | 6.1 | 7.5 | 22.0 | 64.3 |
| Max tps during an interval: | 1,567 | Max | 29.9 | 56.1 | 81.4 | 100.0 |
| Max tps interval time: | 21:19:49 | Max:Avg | 4.9 | 7.5 | 3.7 | 1.6 |
| Total number of Mbytes read: | 25,816 | |||||
| Total number of Mbytes written: | 41,745 | |||||
| Read/Write Ratio: | 0.6 |
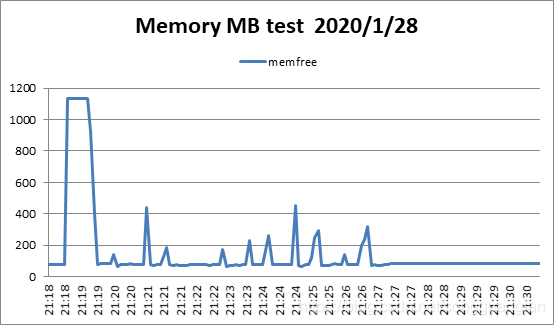
柯西矩阵改进了范德蒙矩阵,同时可得出相似结论。随冗余块的增加,编解码吞吐都在下降,编码吞吐从1345.198704MB/sec降低到198.1768765MB/sec,解码吞吐从885.7057MB/sec降低到140.8307715 MB/sec。编码解码吞吐都在随冗余的增加而下降,但对于此种情况下的编解码吞吐量对比范德蒙矩阵生成矩阵要高出一个水平。编码cpu占有大概在50%左右,解码cpu占大概30%左右。对于磁盘I/O吞吐也维持在1300MB/sec上下,而内存则平均维持在300MB左右。利用柯西矩阵替代范德蒙矩阵,柯西矩阵求逆会改善范德蒙矩阵的求逆运算,使得生成矩阵与矩阵求逆变得简单,能提高编解码的吞吐。
Cauchy_Good
从编解码过程来看,柯西编解码最大的运算量是乘法和加法运算。在范德蒙编码的时候,我们可以采用对数 / 反对数表的方法将乘法运算转换成了加法运算,并且在迦罗华域中,加法运算转换成了 XOR 运算。柯西编解码为了降低乘法复杂度,采用了有限域上的元素都可以使用二进制矩阵表示的原理,将乘法运算转换成了迦罗华域“与运算”和“ XOR 逻辑运算”,提高了编解码效率。从数学的角度来看,在迦罗华有限域中,任何一个GF(2^w)
域上的元素都可以映到 GF(2)二进制域,并且采用一个二进制矩阵的方式表示GF(2^w)
中的元在 GF(2w)域中的生成矩阵为K*(K+m),转换到GF(2)域中,变成(w*k)*(w*(k+m))二进制矩阵。采用域转换的目的是简化GF(2w)域中的乘法运算。在 GF(2)域中,乘法运算变成了逻辑与运算,加法运算变成了 XOR 运算,可以大大降低运算复杂度。和范德蒙编解码中提到的对数 / 反对数方法相比,这种方法不需要构建对数/反对数表,可以支持w为很大的 GF 域空间。
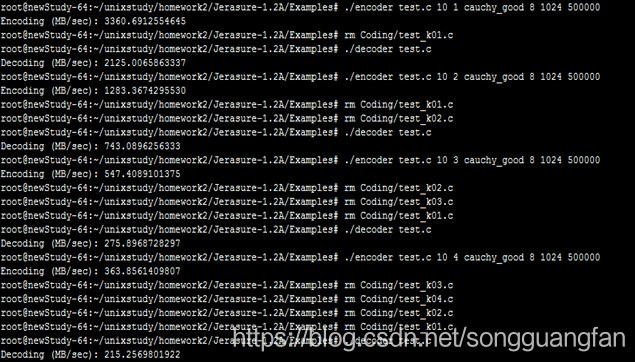
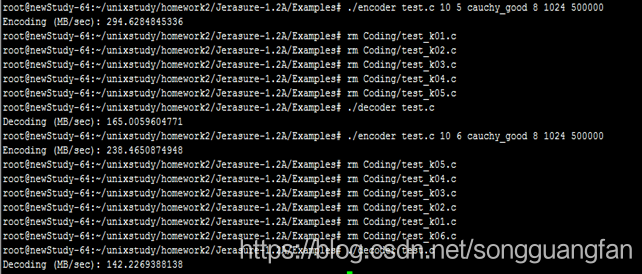
| 冗余块 | 编码吞吐(MB/sec) | 解码吞吐(MB/sec) |
|---|---|---|
| 1 | 3544.594083 | 2095.680832、 |
| 2 | 1257.162896 | 744.9919618 |
| 3 | 545.3146513 | 275.6080565 |
| 4 | 359.1519832 | 215.2569802 |
| 5 | 294.6284845 | 165.0059605 |
| 6 | 238.4650875 | 142.2269388 |
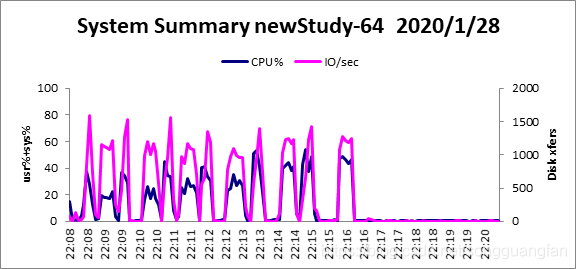
| Total System I/O Statistics | CPU: | User% | Sys% | Wait% | Idle% | |
|---|---|---|---|---|---|---|
| Avg tps during an interval: | 389 | Avg | 5.3 | 7.1 | 22.4 | 65.3 |
| Max tps during an interval: | 1,593 | Max | 9.8 | 33.8 | 84.0 | 100.0 |
| Max tps interval time: | 22:08:47 | Max:Avg | 5.6 | 4.8 | 3.8 | 1.5 |
| Total number of Mbytes read: | 25,833 | |||||
| Total number of Mbytes written: | 42,108 | |||||
| Read/Write Ratio: | 0.6 |
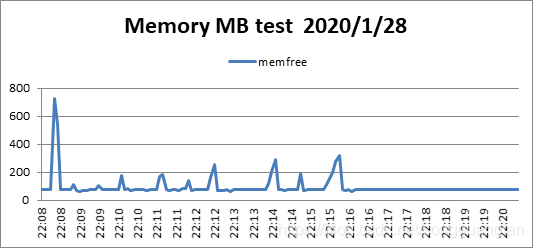
改进后的柯西矩阵改进原始矩阵,同时可得出相似结论。随冗余块的增加,编解码吞吐都在下降,编码吞吐从3544.594083MB/sec降低到238.4650875MB/sec,解码吞吐从2095.680832MB/sec降低到142.2269388MB/sec。编码解码吞吐都在随冗余的增加而下降,但对于此种情况下的编解码吞吐量对比原始矩阵生成矩阵要高出一个水平。但较于基于范德蒙矩阵的矩阵生成方法确实编解码吞吐有较大提高。编码cpu占有平均处于40%左右,解码cpu占有平均处于30%左右。对于磁盘I/O吞吐平均维持在1500MB/sec上下,而内存则维持在200MB左右。与柯西未改进的算法在编解码吞吐与cpu占有上都有一定性能提高,吞吐量在增加,cpu占有降低。在 GF ( 2^w )域中的生成矩阵为 K* ( K+m ),转换到 GF ( 2 )域中,变成了(wk) * (w(k+m)) 二进制矩阵。采用域转换的目的是简化 GF ( 2^w )域中的乘法运算。在 GF ( 2 )域中,乘法运算变成了逻辑与运算,加法运算变成了 XOR 运算,可以大大降低运算复杂度。


