- 1【Unity学习笔记】b站Unity架构课Unity3D 商业化的网络游戏架构(高级/主程级别)_unity3d 商业化的网络游戏架构(高级/主程级别)
- 2地图比例尺与空间分辨率之间的关系_地图比例尺,分辨率,dpi之间的关系
- 3Fastadmin框架,服务器搭建环境
- 4辅警考试怎么搜题答案?八个受欢迎的搜题分享了 #学习方法#学习方法#媒体
- 5模型实战(12)之YOLOv8实现车牌识别:高精度+速度+权重分享_yolo8 predict 识别车牌
- 6模拟退火算法求解TSP问题-python实现_tsp退火算法python
- 7Axure元件库的使用_axure组件库使用
- 8JavaWeb学习路线(总结自尚硅谷雷神SSM|极其详细|思路清晰|适合入门/总复习)
- 9软件测试未来主要发展的5个趋势
- 10uniapp里面tabbar自定义的方法_uniapp 自定义tabbar
动态规划-二维dp数组和滚动数组_滚动数组dp
赞
踩
二维数组
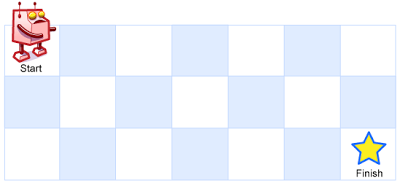
如上图,一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
看到这道题,查找从A点到B点的路径,如果对图论比较熟悉的话,可能第一印象是用图论的深度优先搜索来实现.
func dfs(i int, j int, m int, n int) int {
if i > m || j > n {
return 0
}
if i == m && j == n {
return 1
}
return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n)
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
时间复杂度O(n) = 2^(m+n+1)
从动态规划的角度来思考这个问题,我们要解决的是计算从(0,0)点到(m,n)点的路径数量,根据我们上一张总结的动态规划步骤,
第一步:确定dp数组
dp[m][n]:从(0,0)点到(m,n)点的路径数量
第二步:递推公式
按照题目的描述,每次只能向下或者向右移动一步,所以dp[m][n] = dp[m-1][n] + dp[m][n-1];
第三步:dp数组初始化
dp[0][i] = 1;
dp[j][0] = 1;
第四步:确定遍历顺序
遍历的顺序:从前到后遍历
第五步:举例推导dp数组
实现:
func uniquePaths(m int, n int) int { dp := make([][]int, m); for k := range dp { dp[k] = make([]int, n) } for i := 0; i < m; i ++ { dp[i][0] = 1; } for j := 0; j < n; j ++ { dp[0][j] = 1; } for i := 1; i < m; i ++ { for j := 1; j < n; j ++ { dp[i][j] = dp[i - 1][j] + dp[i][j - 1] } } return dp[m - 1][n - 1] }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
时间复杂度:m * n 空间复杂度:m * n
如果将这个代码在力扣上提交过后, 你会发现,在内存消耗上,你只打败了百分之44的人.意味着有一半以上的人,在空间利用上会比这个方式更好.
那我们的代码是否还有优化的空间呢? 当然也是有的.
滚动数组
动态规划本就是一个记录再利用的高效算法,由于其要记录之前的状态,必然会使用大量空间,要优化动态规划算法的空间,我们必然要合理利用dp数组,有一种优化方法就是利用滚动数组来进行状态转移。
要优化空间复杂度,我们要理解我们dp数组里存的是什么.
先从一个一维的dp数组说起, 斐波拉契数列公式,dp[n] = dp[n - 1] + dp[n - 2], 空间复杂度为O(n);
从这个公式我们可以看出, 在计算dp[n]时,其实只用到了dp[n - 1]和dp[n - 2]. 所以我们只需要定义使用三个变量存储这三个值,依次往后替换,就能达到目的;
代码如下:
func fib(n int) int {
dp := make([]int, 3, 3)
dp[1] = 0
dp[2] = 1
for i := 2; i <=n; i++ {
dp[0] = dp[1]
dp[1] = dp[2]
dp[2] = dp[0] + dp[1]
}
return dp[2]
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
空间复杂度为:O(1),时间复杂度:O(n)
二维的dp数组怎么处理呢? 从上面那个求网格路径数量的代码中,我们可以看到,数据的填充顺序是,初始化,然后一层一层的遍历下去的.
并且根据推导公式 dp[i][j] = dp[i - 1][j] + dp[i][j - 1] , 我们可以使用一个一维数组存放每一层遍历算出来的结果dp[n],到下一层遍历的时候,
dp[n] = dp[n] + dp [n - 1];
公式解析: 等号左边的dp[m]是当前正在遍历的这一层下标为n的位置的路径数量, 右边的dp[n]代表上一层下标为n的位置的路径数量, 而dp[n - 1]是当前正在遍历的这一层的下标为n-1的位置的路径数量.其实与之前的公式是一致的,只是将二维数组缩减为了一维数组.
代码如下:
func uniquePaths(m int, n int) int {
dp := make([]int, n);
for j := 0; j < n; j ++ {
dp[j] = 1;
}
for i := 1; i < m; i ++ {
for j := 1; j < n; j ++ {
dp[j] = dp[j] + dp[j - 1]
}
}
return dp[n - 1]
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
空间复杂度为:O(n),时间复杂度:O(m*n)
提交力扣,恭喜你,在内存消耗上打败了百分之90的人.
参考: https://www.zhihu.com/question/39948290




