AVL树(平衡二叉树):
AVL树本质上是一颗二叉查找树,但是它又具有以下特点:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。在AVL树中任何节点的两个子树的高度最大差别为一,所以它也被称为平衡二叉树。下面是平衡二叉树和非平衡二叉树对比的例图:

平衡因子(bf):结点的左子树的深度减去右子树的深度,那么显然-1<=bf<=1;
AVL树的作用:
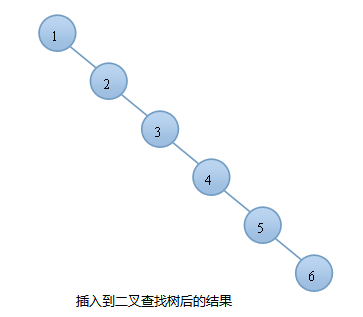
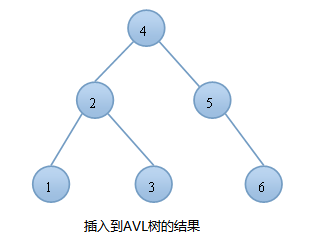
由上图可知,同样的结点,由于插入方式不同导致树的高度也有所不同。特别是在带插入结点个数很多且正序的情况下,会导致二叉树的高度是O(N),而AVL树就不会出现这种情况,树的高度始终是O(lgN).高度越小,对树的一些基本操作的时间复杂度就会越小。这也就是我们引入AVL树的原因
AVL树的基本操作:
AVL树的操作基本和二叉查找树一样,这里我们关注的是两个变化很大的操作:插入和删除!
我们知道,AVL树不仅是一颗二叉查找树,它还有其他的性质。如果我们按照一般的二叉查找树的插入方式可能会破坏AVL树的平衡性。同理,在删除的时候也有可能会破坏树的平衡性,所以我们要做一些特殊的处理,包括:单旋转和双旋转!
AVL树的插入,单旋转的第一种情况---右旋:
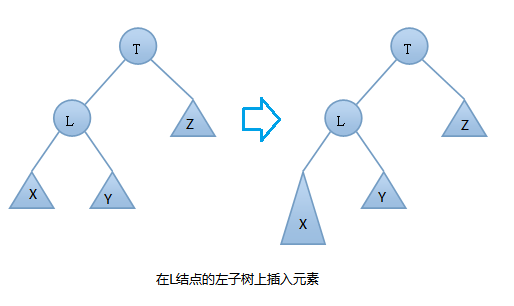
由上图可知:在插入之前树是一颗AVL树,而插入之后结点T的左右子树高度差的绝对值不再 < 1,此时AVL树的平衡性被破坏,我们要对其进行旋转。由上图可知我们是在结点T的左结点的左子树上做了插入元素的操作,我们称这种情况为左左情况,我们应该进行右旋转(只需旋转一次,故是单旋转)。具体旋转步骤是:
T向右旋转成为L的右结点,同时,Y放到T的左孩子上。这样即可得到一颗新的AVL树,旋转过程图如下:
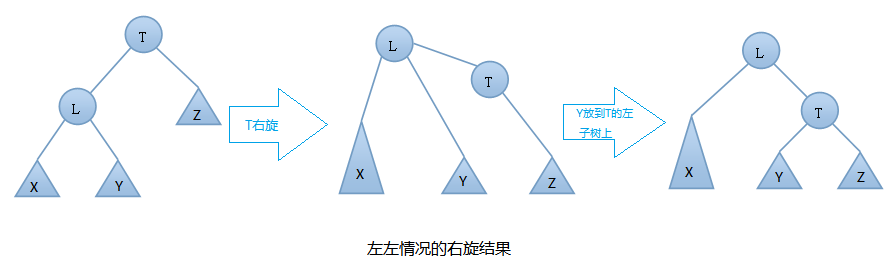
左左情况的右旋举例:
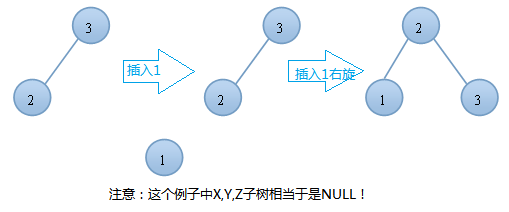
AVL树的插入,单旋转的第一种情况---左旋:
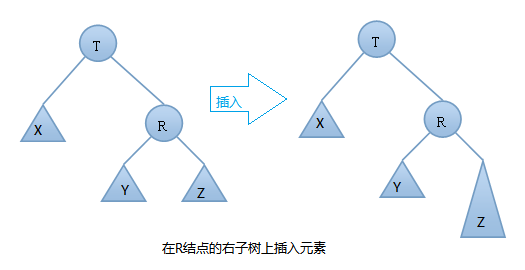
由上图可知:在插入之前树是一颗AVL树,而插入之后结点T的左右子树高度差的绝对值不再 < 1,此时AVL树的平衡性被破坏,我们要对其进行旋转。由上图可知我们是在结点T的右结点的右子树上做了插入元素的操作,我们称这种情况为右右情况,我们应该进行左旋转(只需旋转一次,故事单旋转)。具体旋转步骤是:
T向右旋转成为R的左结点,同时,Y放到T的左孩子上。这样即可得到一颗新的AVL树,旋转过程图如下:
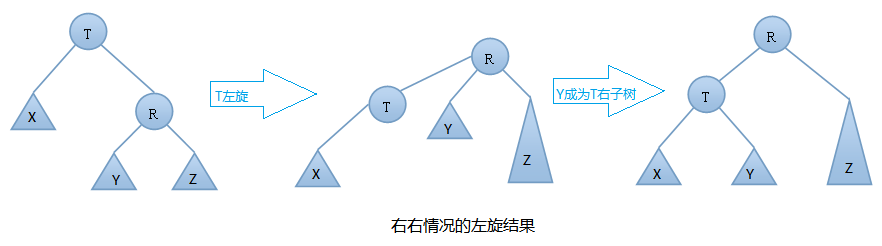
右右情况的左旋举例:
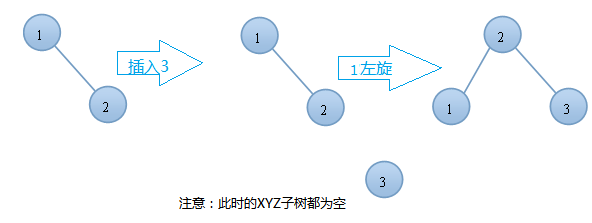
以上就是插入操作时的单旋转情况!我们要注意的是:谁是T谁是L,谁是R还有谁是X,Y,Z!T始终是开始不平衡的左右子树的根节点。显然L是T的左结点,R是T的右节点。X、Y、Y是子树当然也可以为NULL.NULL归NULL,但不能破坏插入时我上面所说的左左情况或者右右情况。
AVL树的插入,双旋转的第一种情况---左右(先左后右)旋:
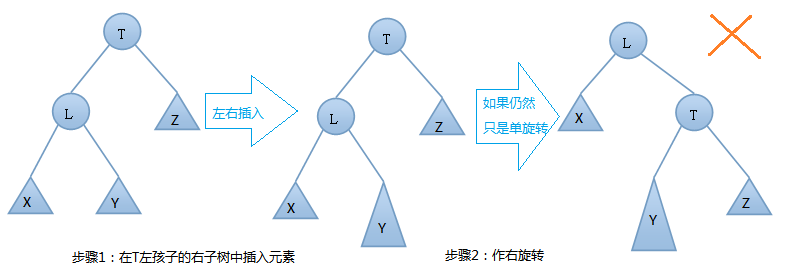
由 上图可知,我们在T结点的左结点的右子树上插入一个元素时,会使得根为T的树的左右子树高度差的绝对值不再 < 1,如果只是进行简单的右旋,得到的树仍然是不平衡的。我们应该按照如下图所示进行二次旋转:
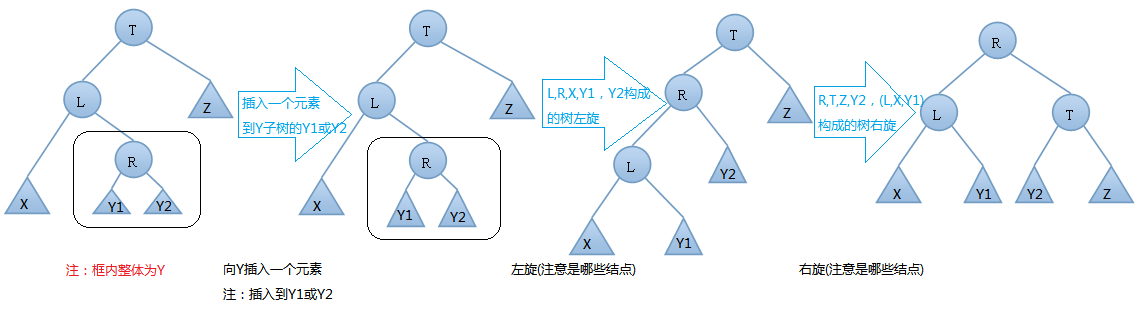
左右情况的左右旋转实例:
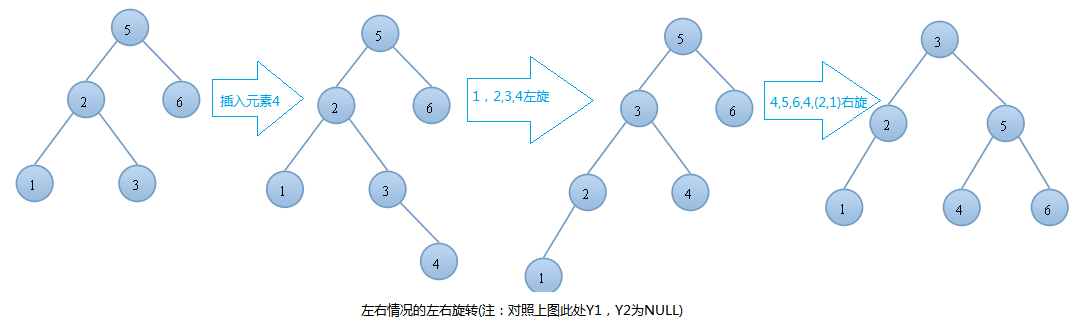
AVL树的插入,双旋转的第二种情况---右左(先右后左)旋:
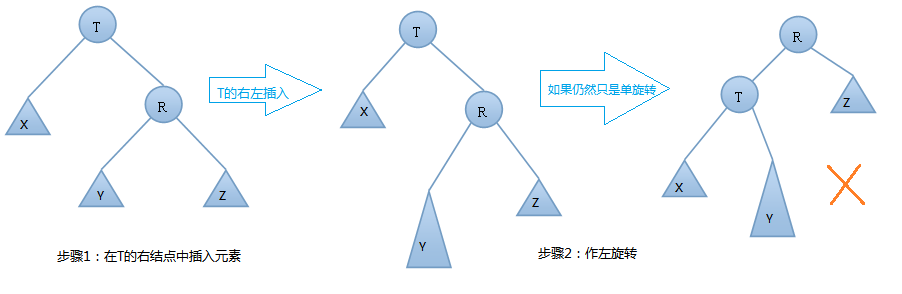
由上图可知,我们在T结点的右结点的左子树上插入一个元素时,会使得根为T的树的左右子树高度差的绝对值不再 < 1,如果只是进行简单的左旋,得到的树仍然是不平衡的。我们应该按照如下图所示进行二次旋转:
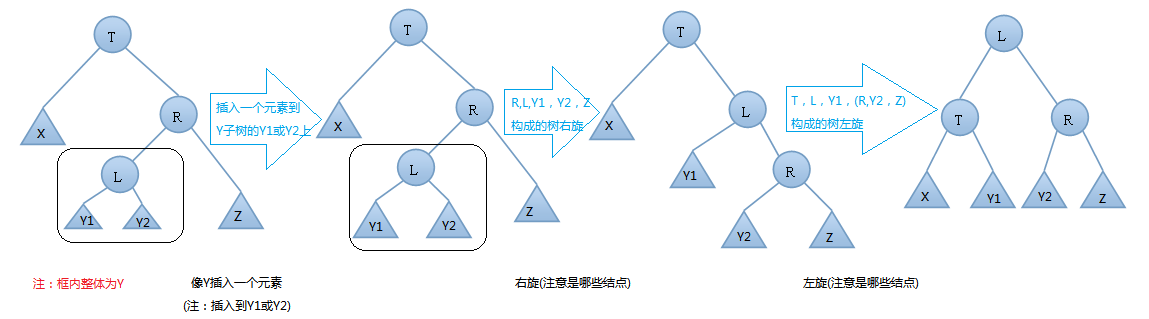
右左情况的右左旋转实例:

AVL树的插入代码实现:(仅供参考)
懂了以上单旋转和双旋转的原理之后,那么代码写起来也就比较简单了,以下是我写的代码,如果有错还望大家不吝指正。(参考数据结构与算法分析-Weiss著)
1 #include <iostream> 2 3 using namespace std; 4 5 #define DataType int 6 7 /* 8 定义AVL树的结构体,链式 9 */ 10 typedef struct AvlNode{ 11 DataType data; 12 AvlNode * m_pLeft; 13 AvlNode * m_pRight; 14 int height; 15 }*AvlTree,*Position,AvlNode; 16 17 //求两个数的最大值 18 int Max(int a,int b) 19 { 20 return a>b?a:b; 21 } 22 //求树的高度 23 int Height( AvlTree T) 24 { 25 if(NULL == T) 26 return -1; 27 else 28 return T->height; 29 } 30 31 //单旋转右旋 32 AvlTree singleRotateWithRight(AvlTree T) 33 { 34 AvlTree L = T->m_pLeft; 35 T->m_pLeft = L->m_pRight; 36 L->m_pRight = T; 37 T->height = Max( Height(T->m_pLeft),Height(T->m_pRight) ) + 1; 38 L->height = Max( Height(L->m_pLeft),Height(L->m_pRight) ) + 1; 39 return L; //此时L成为根节点了(可参考AVL的插入的左左情况的右旋图) 40 } 41 //单旋转左旋 42 AvlTree singleRotateWithLeft(AvlTree T) 43 { 44 AvlTree R = T->m_pRight; 45 T->m_pRight = R->m_pLeft; 46 R->m_pLeft = T; 47 T->height = Max( Height(T->m_pLeft),Height(T->m_pRight) ) + 1; 48 R->height = Max( Height(R->m_pLeft),Height(R->m_pRight) ) + 1; 49 return R; //此时R成为根节点了(可参考AVL的插入的左左情况的左旋图) 50 } 51 //双旋转,先左后右 52 AvlTree doubleRotateWithLeft(AvlTree T) //先左后右 53 { 54 T->m_pLeft = singleRotateWithLeft(T->m_pLeft); 55 return singleRotateWithRight(T); 56 } 57 //双旋转,先右后左 58 AvlTree doubleRotateWithRight(AvlTree T) //先右后左 59 { 60 T->m_pRight = singleRotateWithRight(T->m_pRight); 61 return singleRotateWithLeft(T); 62 } 63 AvlTree AvlTreeInsert(AvlTree T, DataType x) 64 { 65 if(T == NULL) //如果树为空 66 { 67 T = (AvlNode *)malloc(sizeof(struct AvlNode)); 68 if(T) 69 { 70 T->data = x; 71 T->m_pLeft = NULL; 72 T->m_pRight = NULL; 73 T->height = 0; 74 } 75 else 76 { 77 cout << "空间不够" << endl; 78 exit(0); 79 } 80 } 81 else if( x < T->data) //如果插入到T结点的左子树上 82 { 83 T->m_pLeft = AvlTreeInsert(T->m_pLeft,x); //先插入,后旋转 84 if(Height(T->m_pLeft) - Height(T->m_pRight) == 2) //只有可能是这个 85 { 86 if(x < T->m_pLeft->data) //左左情况,只需要右旋转 87 { 88 T = singleRotateWithRight( T ); 89 } 90 else //左右情况,双旋转,先左 91 { 92 T = doubleRotateWithLeft( T ); 93 } 94 } 95 } 96 else if( x > T->data ) 97 { 98 T->m_pRight = AvlTreeInsert(T->m_pRight,x); 99 if(Height(T->m_pRight) - Height(T->m_pLeft) == 2) 100 { 101 if(x > T->m_pRight->data) //右右情况,进行左旋 102 { 103 T = singleRotateWithLeft( T ); 104 } 105 else //左右情况,双旋转,先右 106 { 107 T = doubleRotateWithRight( T ); 108 } 109 } 110 } 111 //如果这个数已经存在,那么不进行插入 112 T->height = Max(Height(T->m_pLeft),Height(T->m_pRight)) + 1; 113 return T; 114 } 115 //递归实现中序遍历 116 void inOrderVisitUseRecur(const AvlTree pCurrent) 117 { 118 if(pCurrent) 119 { 120 inOrderVisitUseRecur(pCurrent->m_pLeft); 121 cout << pCurrent->data << " "; 122 if(pCurrent->m_pLeft) 123 cout << " leftChild: "<<pCurrent->m_pLeft->data; 124 else 125 cout << " leftChild: "<<"NULL" ; 126 if(pCurrent->m_pRight) 127 cout << " rightChild: "<<pCurrent->m_pRight->data; 128 else 129 cout << " rightChild: "<< "NULL"; 130 cout << endl; 131 inOrderVisitUseRecur(pCurrent->m_pRight); 132 } 133 } 134 int main() 135 { 136 AvlTree root = NULL; 137 root = AvlTreeInsert(root,1); 138 root = AvlTreeInsert(root,2); 139 root = AvlTreeInsert(root,3); 140 root = AvlTreeInsert(root,4); 141 root = AvlTreeInsert(root,5); 142 root = AvlTreeInsert(root,6); 143 root = AvlTreeInsert(root,7); 144 root = AvlTreeInsert(root,8); 145 root = AvlTreeInsert(root,9); 146 root = AvlTreeInsert(root,10); 147 root = AvlTreeInsert(root,11); 148 root = AvlTreeInsert(root,12); 149 root = AvlTreeInsert(root,13); 150 root = AvlTreeInsert(root,14); 151 root = AvlTreeInsert(root,15); 152 inOrderVisitUseRecur(root); 153 return 0; 154 }


