leetcode 797. 所有可能的路径（C++、java）_有向无环图 leetcode

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

二维数组的第 i 个数组中的单元都表示有向图中 i 号节点所能到达的下一些节点，空就是没有下一个结点了。

译者注：有向图是有方向的，即规定了 a→b 你就不能从 b→a 。

示例 1：

输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例 2：

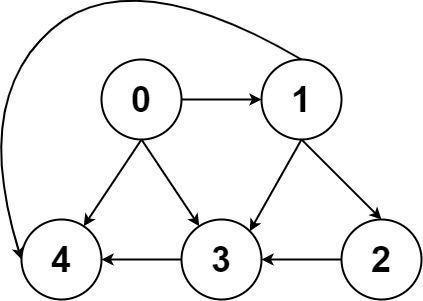
输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

示例 3：

输入：graph = [[1],[]]
输出：[[0,1]]

示例 4：

输入：graph = [[1,2,3],[2],[3],[]]
输出：[[0,1,2,3],[0,2,3],[0,3]]

示例 5：

输入：graph = [[1,3],[2],[3],[]]
输出：[[0,1,2,3],[0,3]]

提示：

• n == graph.length
• 2 <= n <= 15
• 0 <= graph[i][j] < n
• graph[i][j] != i（即，不存在自环）
• graph[i] 中的所有元素 互不相同
• 保证输入为 有向无环图（DAG）

C++

class Solution {
public:
    void dfs(vector <vector<int>> &res, vector<int> &tmp, int k) {
        if (k == graph.size() - 1) {
            res.push_back(tmp);
            return;
        }
        vector<int> vec = graph[k];
        for (int i = 0; i < vec.size(); i++) {
            tmp.push_back(vec[i]);
            dfs(res, tmp, vec[i]);
            tmp.pop_back();
        }
    }
 
    vector <vector<int>> allPathsSourceTarget(vector <vector<int>> &graph) {
        this->graph = graph;
        vector <vector<int>> res;
        vector<int> tmp;
        tmp.push_back(0);
        dfs(res, tmp, 0);
        return res;
    }
 
private:
    vector <vector<int>> graph;
};

java

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    int[][] g;
    int n;
    List<Integer> tmp = new ArrayList<>();
 
    public void dfs(int k) {
        if (k == n - 1) {
            res.add(new ArrayList<>(tmp));
            return;
        }
        int[] vec = g[k];
        for (int i = 0; i < vec.length; i++) {
            tmp.add(vec[i]);
            dfs(vec[i]);
            tmp.remove(tmp.size() - 1);
        }
    }
 
    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        g = graph;
        n = graph.length;
        tmp.add(0);
        dfs(0);
        return res;
    }
}