KAN: Kolmogorov–Arnold Networks 文章理解_kan使用样例

 摘要

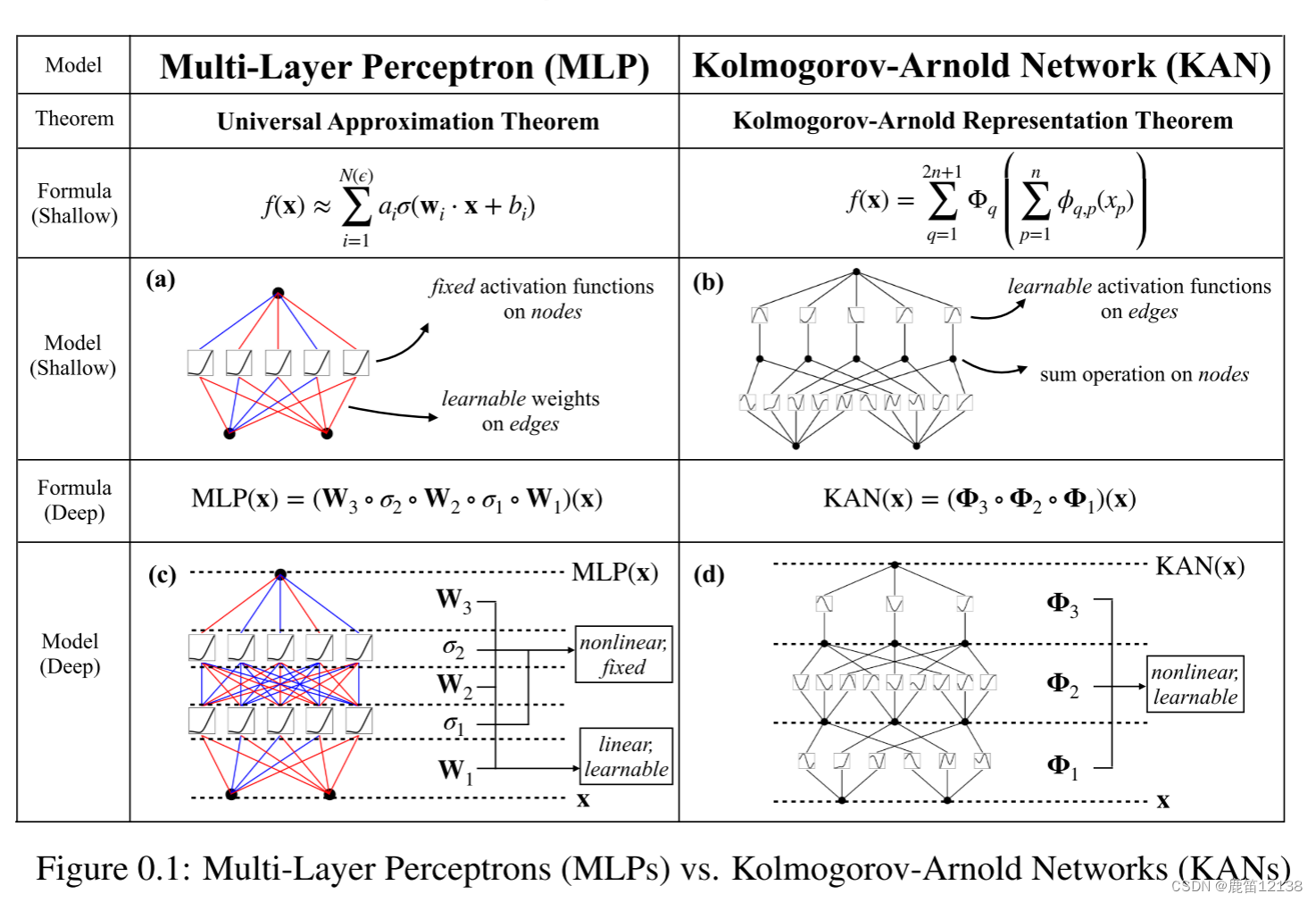
受Kolmogorov-Arnold表示定理的启发，我们提出了Kolmogorov-Arnold网络(KANS)作为多层感知器(MLP)的有前途的替代方案。MLP在节点(“神经元”)上有固定的激活函数，而KANS在边上有可学习的激活函数(“权重”)。KANS根本没有线性权重--每个权重参数都被参数化为样条线的单变量函数所代替。我们表明，这个看似简单的改变使KANS在准确性和可解释性方面优于MLP。在精度方面，在数据拟合和偏微分方程求解中，小得多的KAN可以获得与大得多的MLP相当或更好的精度。从理论和经验上看，KANS比MLP具有更快的神经标度律。在可解释性方面，KANS可以直观地可视化，并可以很容易地与人类用户交互。通过数学和物理的两个例子，坎斯被证明是有用的“合作者”，帮助科学家(重新)发现数学和物理规律。KANS根本没有线性权重矩阵，取而代之的是，每个权重参数都被一个可学习的一维函数代替，该函数被参数化为样条线。Kans的节点只是简单地对输入信号求和，而不应用任何非线性。人们可能会担心KANS太贵了，因为每个MLP的权重参数都变成了Kan的样条函数。幸运的是，KAN通常允许的计算图比MLP小得多。例如，对于偏微分方程组的求解，2层宽度为10的 Kan比4层宽度100的MLP的精度高100倍，参数效率高100倍(100比10000个参数)

原本的核心公式中一个是一维转化实数函数，一个是实数转化函数

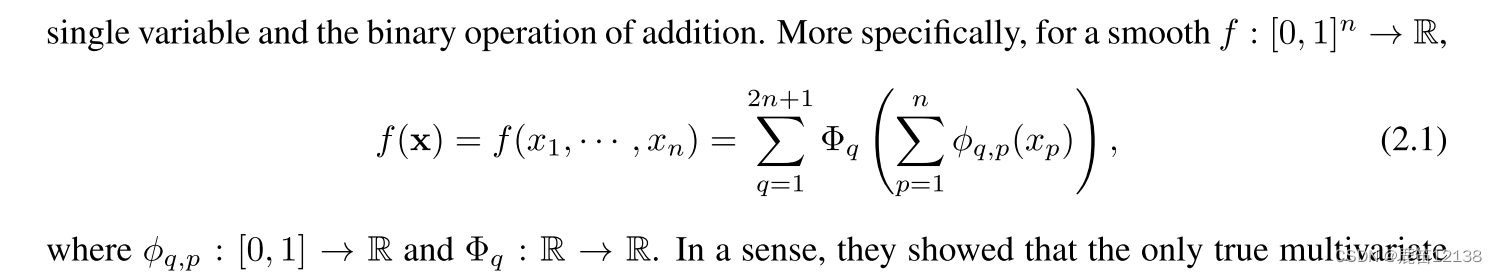
核心网络结构

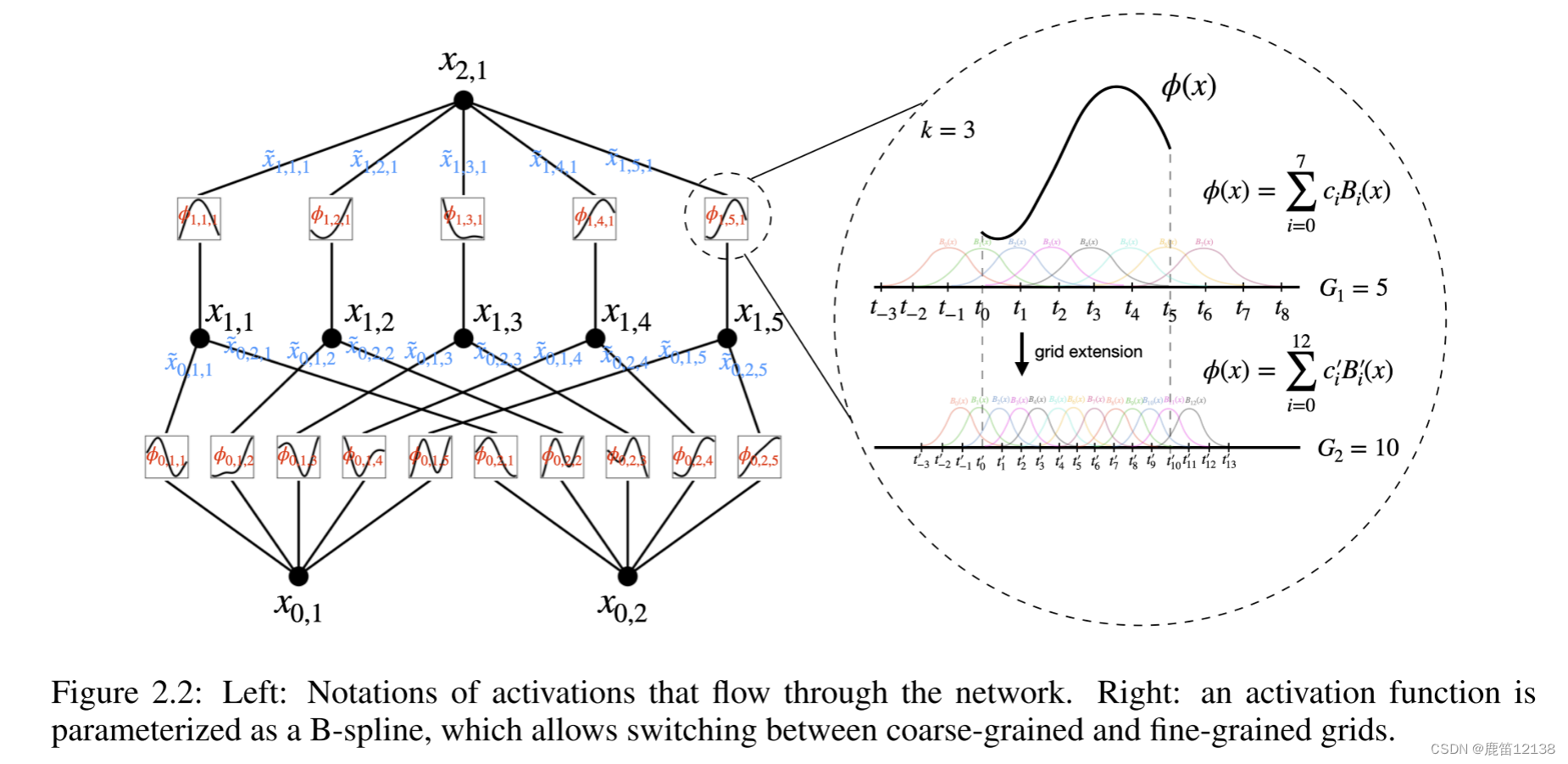
对于图2.2中左半图：

方块表示一个激活函数，实心点表示一个具体的神经元，一个基础的KAN包含有三层神经元和两个接连部分：第一部分，输入是n维度，输出是2n+1维度；第二个部分是输入2n+1，输出为1（这里的维度是指神经元个数）；激活函数构成的矩阵就是每一个链接部分就是一个单独的激活函数矩阵。

对于图片2.2右半图：

其中是根据基础函数和样条函数计算得来的，大多数时候Spline(X)被参数化为B-Spline的线性组合（2.12）初始化的时候Spline(X)≈0，w为Xavier初始化矩阵。
公式2.12中的ci值是可以训练的，Bi（x）是b样条函数B-spline，不理解可以去看看这篇博客

样条曲线曲面-3：BSpline的原理 - 知乎

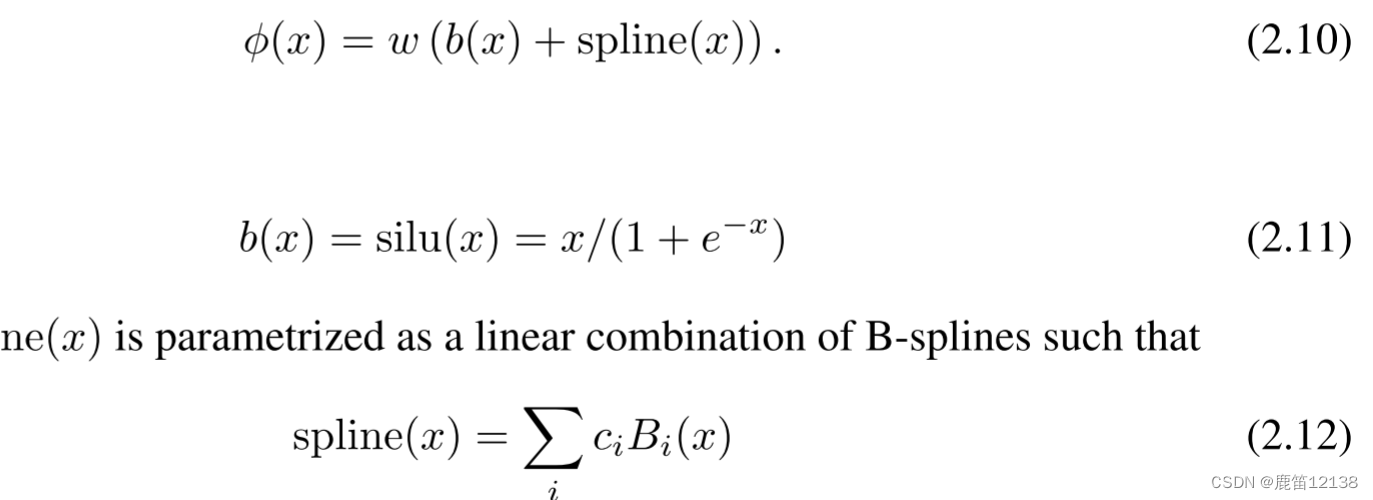
通过不断细化Bi函数的区间，去更新参数，样条就是下面这样一个个彩色小曲线在整个采样区间中的部分区域存在，通过不断增加固定长度上的彩色曲线的数量来更好的模拟函数的样子，有点类似于用更多的点拟合一个函数的意思

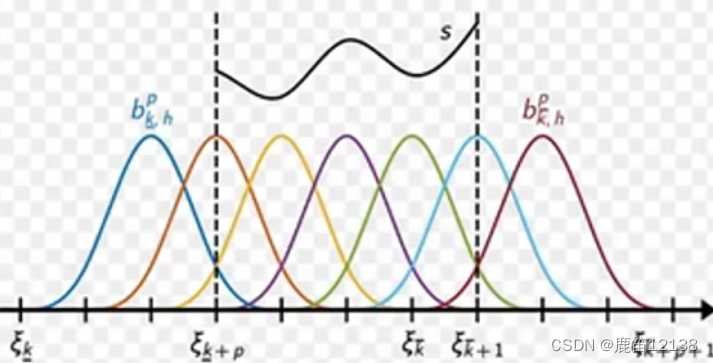
利用最小二乘更新新的cj

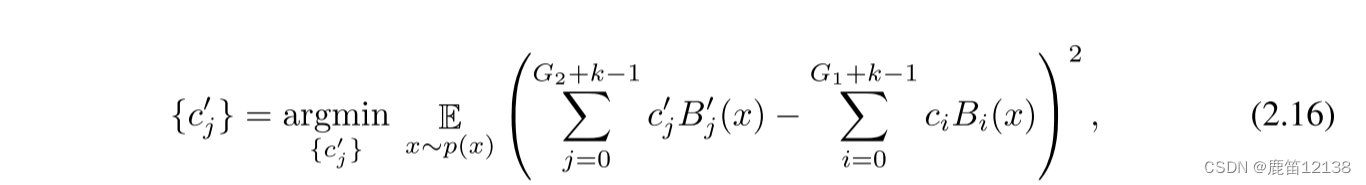
理解样例

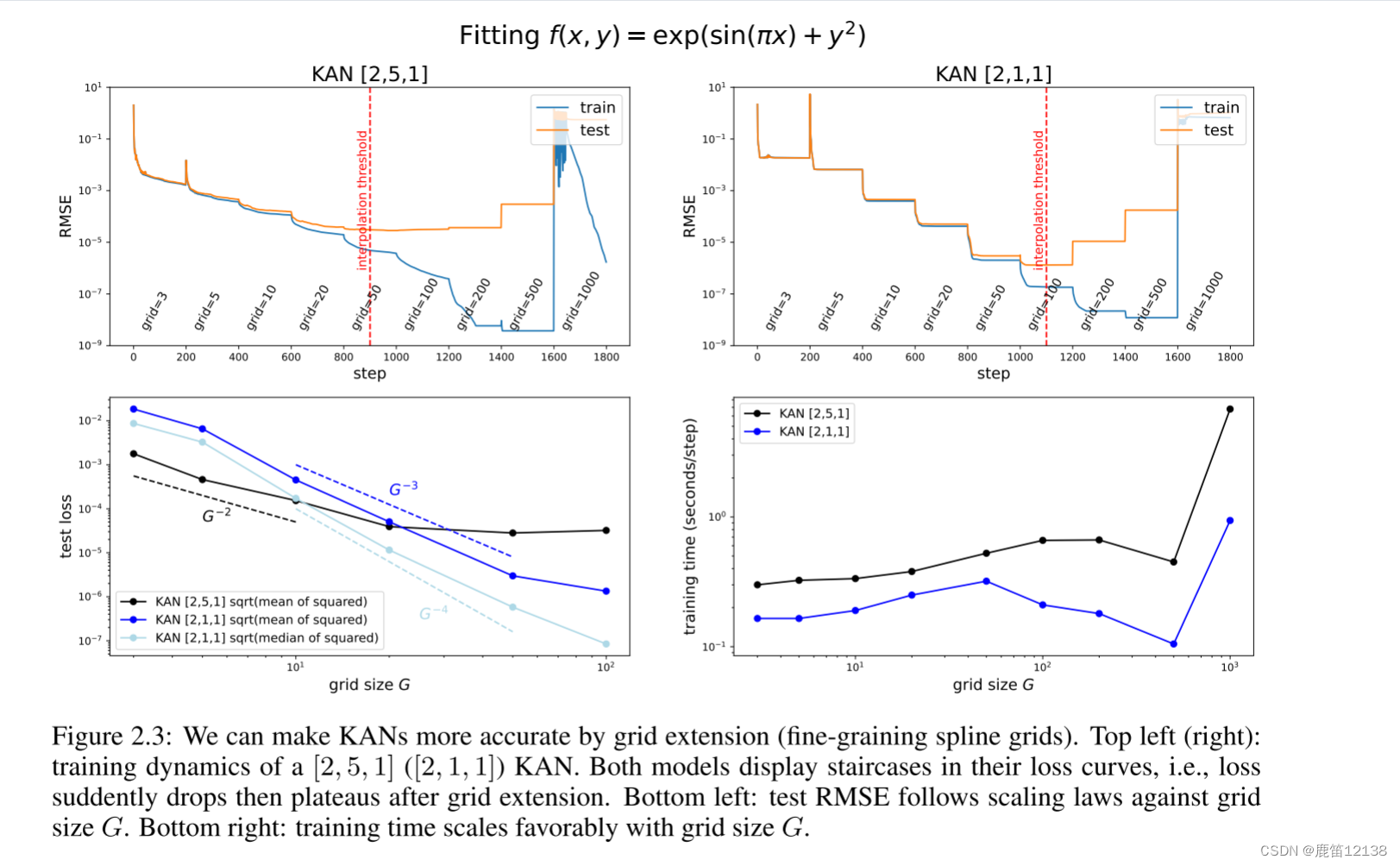
我们用一个玩具例子f(x，y)=exp(sin(πx)+y2)来演示网格扩展的效果。在图2.3(左上角)中，我们显示了[2，5，1]kan的训练和测试RMSE。栅格点的数量从3开始，每200个LBFGS（优化器）步长增加到一个更大的值，最终得到1000个栅格点。很明显，每次发生细粒化时，训练损失比以前下降得更快(除了具有1000个点的最细网格，其中优化停止工作可能是因为糟糕的损失景观)。然而，由于偏差-方差权衡(不足与过适应)，测试损失首先下降，然后上升，呈现U型。我们推测，当参数数目与数据点数目匹配时，最优测试损失是在内插门限处获得的。由于我们的训练样本是1,000个，而a[2，5，1]Kan的总参数是15G(G是网格间隔的数目)，我们预计内插阈值为G=1000/15≈67，这与我们的实验观察值G∼50大致一致。

对于一个函数用kan去逼近会发现简单的kan反而有可能取得一个更好的效果。如下图中的右边下降明显比左边更多一些，区间点grid增加后下降更规整

简化技术

为了满足找寻位置样本集合中最好的拟合函数，就希望可以自动去寻找一个最匹配的模型样例
这个想法是从一个足够大的Kan开始，然后用L1稀疏正则化训练它，然后进行剪枝

因为这里没有一个权重w只有激活函数，所以需要对于激活函数的正则化做L1新的定义见下

当我们可视化Kan时，为了获得对维度的感知，我们将激活函数的透明度设置为与tanh(β,A，i，j)成比例，其中β=3。因此，小幅度的函数似乎淡出，使我们能够专注于重要的函数。

在使用稀疏化惩罚进行训练后，我们可能还希望将网络修剪为更小的子网络。我们在节点级别(而不是边缘级别)稀疏KAN。对于每个节点(例如第l层中的第i个神经元)，我们定义其传入和传出分数当小于某与阈值才被修剪掉

这一步是怎么确定某个函数近似一个真实函数呢？

基于上面的步骤我们找了比较重要的函数曲线并去了噪声，于是观察线形状类似于什么，比如可能像cos，sin这种基础函数，那么就用这些函数来近似曲线。然而，我们不能简单地将激活函数设置为精确的符号公式，因为它的输入和输出可能有移位和标度。因此，我们从样本中获得激活前的x和激活后的y，并拟合仿射参数(a，b，c，d)，使得y≈cf(ax+b)+d。

重中之重：实际操作的例子

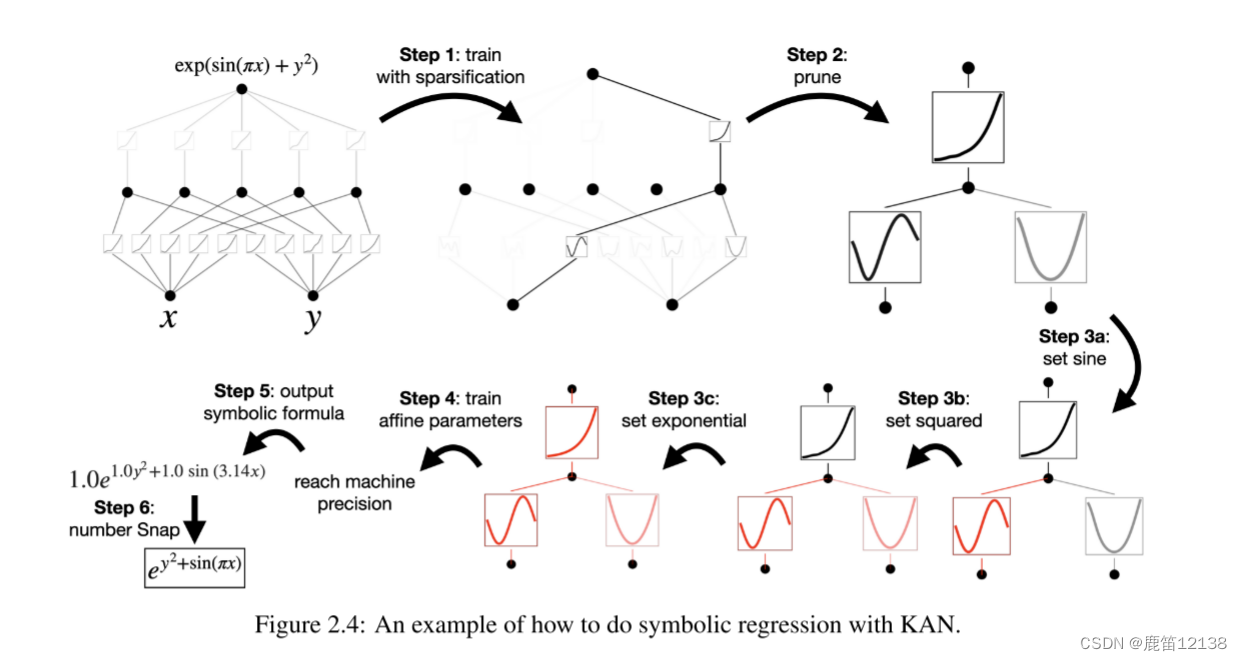
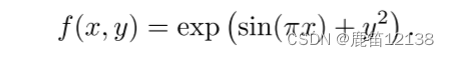
对于上面这个函数利用kan做一个拟合

第一步：使用稀疏化进行训练。从一个完全连通的[2，5，1]看板出发，用稀疏化正则化训练可以使其相当稀疏。隐藏层中的5个神经元中有4个似乎毫无用处，因此我们想要将它们修剪掉

第二步：修剪。自动修剪被认为是丢弃所有隐藏的神经元，留下一个Kan[2，1，1]。激活函数似乎是已知的符号函数。

第三步：设置符号函数。假设用户可以通过凝视Kan图正确地猜测这些符号公式，他们可以设置，在用户没有领域知识或不知道这些激活函数可能是哪些符号函数的情况下，我们提供了函数suggest_symbol来建议符号候选函数

第四步：进一步培训。在对网络中的所有激活函数进行符号化后，唯一剩下的参数就是仿射参数。我们继续训练这些仿射参数，当我们看到损失下降到机器精度时，我们知道我们找到了正确的符号表达式。

第五步：输出符号公式。使用SYMPY计算输出节点的符号公式。用户得到1.0e1.0y2+1.0sin(3.14x)，这是真正的答案(我们只显示了π的两个小数)。

其他实验

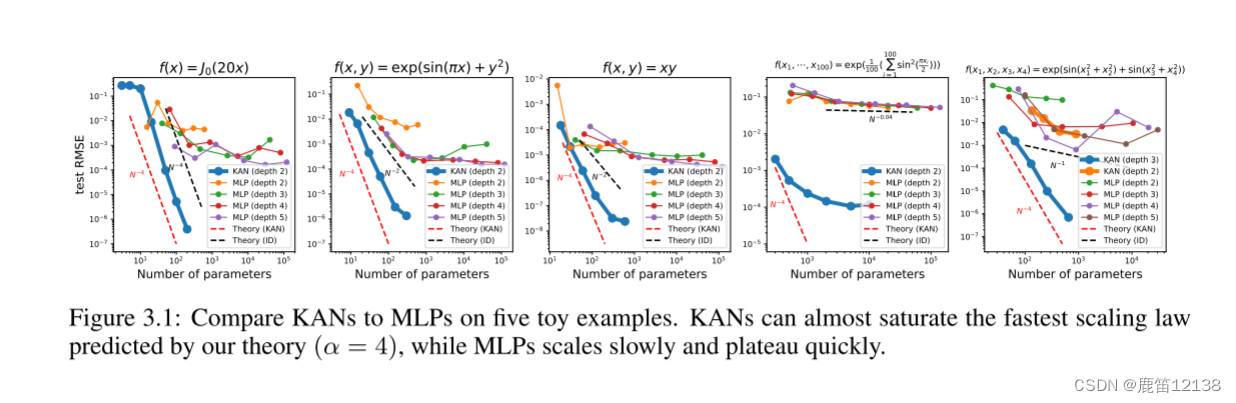
这里有个好玩的是图4，是利用【100,1,1】做的，比MLP要好很多，难到说高维度反而好用？另外就是模型2层Kan[4，9，1]的性能比3层Kan形状[4，2，2，1]差得多。可以思考一下为啥都是越深越好用。

后面还做了大量关于数学、物理公式拟合的实验对比都是kan好一点

灾难遗忘问题

众所周知，MLP有遗忘问题，有各种各样的尝试去保留更多的信息，从RNN到LSTM到transformer模型，KAN则可以在简单问题上规避这个问题。注意这里用了简单因为实验实在是比较简单。

实验里是五个驼峰的函数，可以看到KAN到最后是完美记住每个段落了，但MLP明显对dnagqian

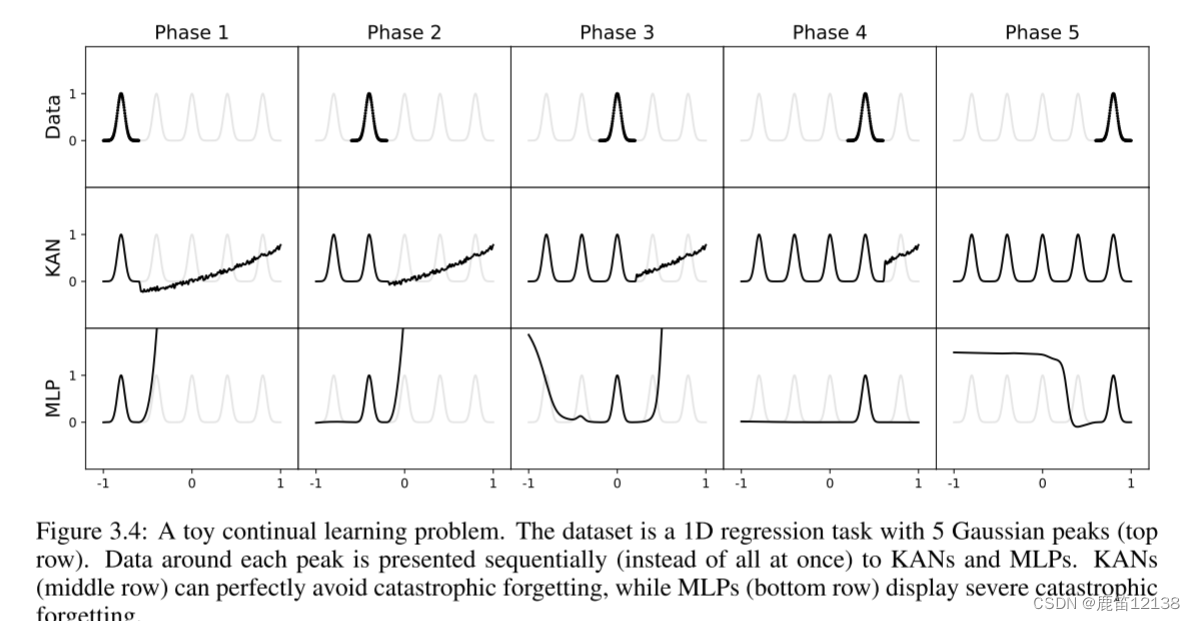
总结：本人只是站在一个KAN是否可以用在未来神经网路去看，很多数学上的推导与验证属实望尘莫及

优点：

1.参数小

2.可与人交互，解释性强

3.AI基座多了一种可以考虑的探索方向，不是单纯的以数据量为驱动发展，如果后续验证可行可能会出现以小博大的好戏

缺点：

1.KAN的小参数优势，其实是更多的探索计算量带来的，这也是训练慢的原因

2.中间有太多的不确定性了，和MLP相比，KAN就像需要精心照顾的花朵，你是可以进行很多调试，甚至是可视化的，但也意味着，在更复杂的环境下去使用KAN也变得非常有挑战。

3.关于遗忘问题，还是持有一个怀疑的态度，因为存在样条函数去模拟整个f，并用多段的方式去记录，使得在简单环境下，f是不会被遗忘的，函数复杂后呢，不太能被样条函数拟合的时候呢或者说不能被很好的拟合的时候呢，还是会有一部分东西被舍弃

4.应用场景，作者在公式推导、函数逼近上都做出了有力证明，但是一切的前提都是复杂函数可以被分解为多元函数可以如何被一组更简单的函数表示。

5.现阶段和GPU的适配有问题